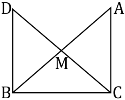
Question 8:
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is
joined to M and produced to a point D such that DM = CM. Point D is joined to point
B (see the given figure). Show that:
(i) ∆AMC ≅ ∆BMD
(ii) ∠DBC is a right angle.
(iii) ∆DBC ≅ ∆ACB
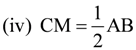
Answer:
(i) In ∆AMC and ∆BMD,
AM = BM (M is the mid-point of AB)
∠AMC = ∠BMD (Vertically opposite angles)
CM = DM (Given)
∆AMC ≅ ∆BMD (By SAS congruence rule)
AC = BD (By CPCT)
And, ∠ACM = ∠BDM (By CPCT)
(ii) ∠ACM = ∠BDM
However, ∠ACM and ∠BDM are alternate interior angles.
Since alternate angles are equal,
It can be said that DB || AC
∠DBC + ∠ACB = 180º (Co-interior angles)
∠DBC + 90º = 180º
∠DBC = 90º
(iii) In &DBC and &ACB,
DB = AC (Already proved)
∠DBC = ∠ACB (Each 90 )
BC = CB (Common)
∆DBC ≅ ∆ACB (SAS congruence rule)
(iv) ∆DBC ≅ ∆ACB
AB = DC (By CPCT)
AB = 2 CM

Latest Govt Job & Exam Updates: