Question 1:
Show that in a right angled triangle, the hypotenuse is the longest side.
Answer:
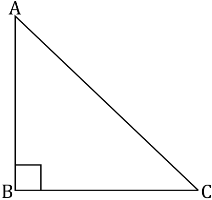
Let us consider a right-angled triangle ABC, right-angled at B.
In ∆ABC,
∠A + ∠B + ∠C = 180° (Angle sum property of a triangle)
∠A + 90º + ∠C = 180°
∠A + ∠C = 90°
Hence, the other two angles have to be acute (i.e., less than 90º).
∠B is the largest angle in &ABC.
∠B > ∠A and ∠B > ∠C
AC > BC and AC > AB
[In any triangle, the side opposite to the larger (greater) angle is longer.]
Therefore, AC is the largest side in ∆ABC.
However, AC is the hypotenuse of ∆ABC. Therefore, hypotenuse is the longest side in
a right-angled triangle.
Latest Govt Job & Exam Updates: