Question 1:
Solve the following pair of linear equations by the elimination method and the substitution method:
(i) x + y = 5 and 2x – 3y = 4
(ii) 3x + 4y = 10 and 2x – 2y = 2
(iii) 3x + 4y = 10 and 2x – 2y = 2

Answer:
(i) By elimination method
x + y = 5 (1)
2x − 3y = 4 (2)
Multiplying equation (1) by 2, we obtain
2x + 2y = 10 (3)
Subtracting equation (2) from equation (3), we obtain
5y = 6
y = 6/5 (4)
Substituting the value in equation (1), we obtain

By substitution method
From equation (1), we obtain
x = 5 − y (5)
Putting this value in equation (2), we obtain
2(5 − y) − 3y = 4
−5y = −6
y = 6/5
Substituting the value in equation (5), we obtain

(ii) By elimination method
3x + 4y = 10 (1)
2x − 2y = 2 (2)
Multiplying equation (2) by 2, we obtain
4x − 4y = 4 (3)
Adding equation (1) and (3), we obtain
7x = 14
x = 2 (4)
Substituting in equation (1), we obtain
6 + 4y = 10
4y = 4
y = 1
Hence, x = 2, y = 1
By substitution method
From equation (2), we obtain
x = 1 + y (5)
Putting this value in equation (1), we obtain
3(1 + y) + 4y = 10
7y = 7
y = 1
Substituting the value in equation (5), we obtain
x = 1 + 1 = 2
∴ x = 2, y = 1
(iii) By elimination method
3x − 5y − 4 = 0 (1)
9x = 2y + 7
9x − 2y − 7 = 0 (2)
Multiplying equation (1) by 3, we obtain
9x − 15y − 12 = 0 (3)
Subtracting equation (3) from equation (2), we obtain
13y = −5
y = −5/13 (4)
Substituting in equation (1), we obtain

By substitution method
From equation (1), we obtain
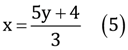
Putting this value in equation (2), we obtain

(iv)By elimination method

Subtracting equation (2) from equation (1), we obtain
5y = −15
y = −3 (3)
Substituting this value in equation (1), we obtain
3x − 12 = −6
3x = 6
x = 2
Hence, x = 2, y = −3
By substitution method
From equation (2), we obtain

Latest Govt Job & Exam Updates: