Question 7:
Let A (4, 2), B (6, 5) and C (1, 4) be the vertices of ΔABC.
(i) The median from A meets BC at D. Find the coordinates of point D.
(ii) Find the coordinates of the point P on AD such that AP: PD = 2:1
(iii) Find the coordinates of point Q and R on medians BE and CF respectively such that BQ: QE = 2:1 and CR: RF = 2:1.
(iv) What do you observe?
(v) If A(x1, y1), B(x2, y2), and C(x3, y3) are the vertices of ΔABC, find the coordinates of the centroid of the triangle.
Answer:

(i) Median AD of the triangle will divide the side BC in two equal parts.
Therefore, D is the mid-point of side BC.
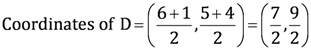
(ii) Point P divides the side AD in a ratio 2:1.

(iii) Median BE of the triangle will divide the side AC in two equal parts.
Therefore, E is the mid-point of side AC.
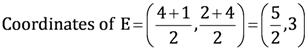
Point Q divides the side BE in a ratio 2:1.

Median CF of the triangle will divide the side AB in two equal parts. Therefore, F is the mid-point of side AB.
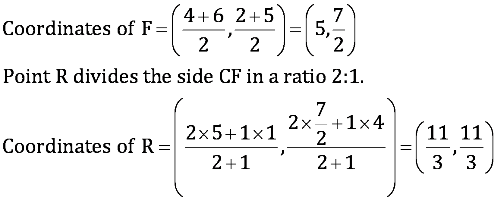
(iv) It can be observed that the coordinates of point P, Q, R are the same.
Therefore, all these are representing the same point on the plane i.e., the centroid of the triangle.
(v) Consider a triangle, ΔABC, having its vertices as A(x1, y1), B(x2, y2), and C(x3, y3).
Median AD of the triangle will divide the side BC in two equal parts. Therefore, D is the mid-point of side BC.

Latest Govt Job & Exam Updates: