Question 14:
Find the real numbers x and y if (x – iy) (3 + 5i) is the conjugate of −6 – 24i.
Answer
Let z = (x – iy) (3 + 5i)
z = 3x + 5xi – 3yi – 5yi2 = 3x + 5xi – 3yi + 5y = (3x + 5y) + i(5x – 3y)
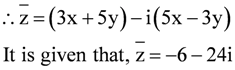
∴ (3x + 5y) – i(5x – 3y) = −6 – 24i
Equating real and imaginary parts, we obtain
3x + 5y = −6 ….(i)
5x – 3y = 24 ….(ii)
Multiplying equation (i) by 3 and equation (ii) by 5 and then adding them, we obtain 9x + 15y = −18

Putting the value of x in equation (i), we obtain
3(3) + 5y = −6
⇒ 5y = −6 – 9 = −15
⇒ y = −3
Thus, the values of x and y are 3 and −3 respectively.
Latest Govt Job & Exam Updates: