Question 16:

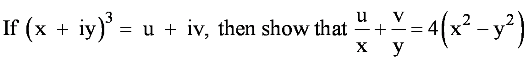
Answer

(x + iy)³ = u + iv

⇒ x³ + (iy)³ + 3 ∙ x ∙ iy(x + iy) = u + iv

⇒ x³ + i³y³ + 3x²yi + 3xy²i² = u + iv

⇒ x³ – iy³ + 3x²­yi− 3xy² = u + iv

⇒ (x³ – 3xy²) + i(3x²y – y³) = u + iv

On equating real and imaginary parts, we obtain

u = x³ – 3xy², v = 3x²y – y³

Latest Govt Job & Exam Updates:

View Full List ...