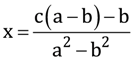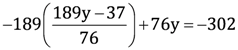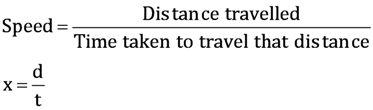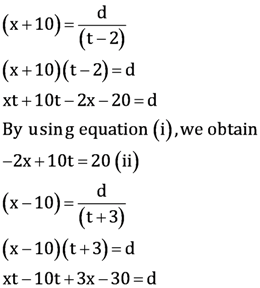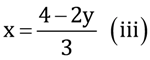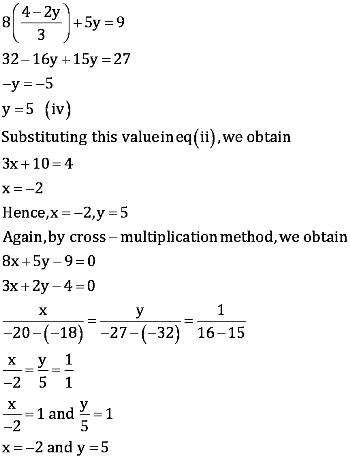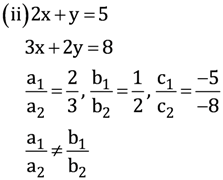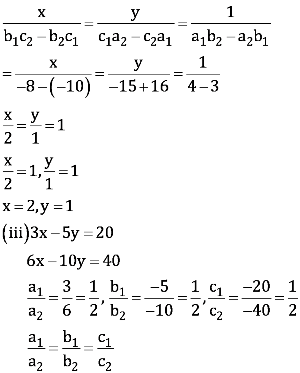CBSE Class X

Question 4:

Find two consecutive positive integers, sum of whose squares is 365.

Answer:

Let the consecutive positive integers be x and x + 1.

Given that x² + (x + 1)² = 365

⇒ x² + x² +1 + 2x = 365

⇒ 2x² + 2x – 364 = 0

⇒ x² + x – 182 = 0

⇒ x² + 14x – 13x – 182 = 0

⇒x(x + 14) –13(x + 14) = 0

⇒(x + 14) (x – 13) = 0

Either x + 14 = 0 or x − 13 = 0, i.e., x = −14 or x = 13

Since the integers are positive, x can only be 13.

∴ x + 1 = 13 + 1 = 14

Therefore, two consecutive positive integers will be 13 and 14.

Question 3:

Find two numbers whose sum is 27 and product is 182.

Answer:

Let the first number be x and the second number is 27 − x.

Therefore, their product = x (27 − x)

It is given that the product of these numbers is 182.

Therefore, x(27 – x) = 182

⇒ x² – 27x + 182 = 0

⇒ x² – 13x – 14x + 182 = 0

⇒ x(x – 13) –14 (x – 13) = 0

⇒ (x – 13) (x – 14) = 0

Either x – 13 = 0 or x − 14 = 0

i.e., x = 13 or x = 14

If first number = 13, then

Other number = 27 − 13 = 14

If first number = 14, then

Other number = 27 − 14 = 13

Therefore, the numbers are 13 and 14.

Question 2:

(i) John and Jivanti together have 45 marbles. Both of them lost 5 marbles each, and the product of the number of marbles they now
have is 124. Find out how many marbles they had to start with.

(ii) A cottage industry produces a certain number of toys in a day. The cost of production of each toy (in rupees) was found to be 55 minus
the number of toys produced in a day. On a particular day, the total cost of production was Rs 750. Find out the number of toys produced
on that day.

Answer:

(i) Let the number of John’s marbles be x.

Therefore, number of Jivanti’s marble = 45 − x

After losing 5 marbles,

Number of John’s marbles = x − 5

Number of Jivanti’s marbles = 45 − x − 5 = 40 − x

It is given that the product of their marbles is 124.

∴ (x – 5) (40 – x) = 124

⇒ x² – 45x + 324 = 0

⇒ x² – 36x – 9x + 324 = 0

⇒ x(x – 36) −9 (x – 36) = 0

⇒ (x – 36) (x – 9) = 0

Either x – 36 = 0 or x – 9 = 0

i.e., x = 36 or x = 9

If the number of John’s marbles = 36,

Then, number of Jivanti’s marbles = 45 − 36 = 9

If number of John’s marbles = 9,

Then, number of Jivanti’s marbles = 45 − 9 = 36

(ii) Let the number of toys produced be x.

∴ Cost of production of each toy = Rs (55 − x)

It is given that, total production of the toys = Rs 750

∴ x(55 – x) = 750

⇒ x² −  55x + 750 = 0

⇒ x² – 25x – 30x + 750 = 0

⇒ x(x – 25) – 30 (x – 25) = 0

⇒ (x – 25) (x – 30) = 0

Either x – 25 = 0 or x – 30 = 0

i.e., x = 25 or x = 30

Hence, the number of toys will be either 25 or 30.

Question 1:

Find the roots of the following quadratic equations by factorisation :

   (i) x² – 3x – 10 = 0                        (ii) 2x² + x – 6 = 0

 (v) 100 x2 – 20x + 1 = 0

Answer:

(v) 100x² – 20x + 1

      = 100x² – 10x – 10x + 1

      = 10x (10x – 1) –1 (10x – 1)

      = (10x – 1)²

Roots of this equation are the values for which (10x – 1)² = 0

Therefore, (10x – 1) = 0 or (10x – 1) = 0

i.e., x = 1/10 or x = 1/10

Question 2:

Represent the following situations in the form of quadratic equations.

(i) The area of a rectangular plot is 528 m². The length of the plot (in metres) is one more than twice its breadth. We need to find the length
and breadth of the plot.

(ii) The product of two consecutive positive integers is 306. We need to find the integers.

(iii) Rohan’s mother is 26 years older than him. The product of their ages (in years) 3 years from now will be 360. We would like to find
Rohan’s present age.

(iv) A train travels a distance of 480 km at a uniform speed. If the speed had been 8 km/h less, then it would have taken 3 hours more to
cover the same distance. We need to find the speed of the train.

Answer:

(i) Let the breadth of the plot be x m.

Hence, the length of the plot is (2x + 1) m.

Area of a rectangle = Length × Breadth

∴ 528 = x (2x + 1)

⇒ 2x² + x – 528 = 0

(ii) Let the consecutive integers be x and x + 1.

It is given that their product is 306.

∴ x(x + 1) = 306 ⇒ x² + x – 306 = 0

(iii) Let Rohan’s age be x.

Hence, his mother’s age = x + 26

3 years hence,

Rohan’s age = x + 3

Mother’s age = x + 26 + 3 = x + 29

It is given that the product of their ages after 3 years is 360.

∴ (x + 3) (x + 29) = 360

⇒ x² + 32x – 273 = 0

(iv) Let the speed of train be x km/h.

Time taken to travel 480 km = 480/x hrs

In second condition, let the speed of train = (x – 8) km/h

It is also given that the train will take 3 hours to cover the same distance.

Therefore, time taken to travel 480 km

 

Question 1:

Check whether the following are quadratic equations:

(i) (x + 1)² = 2(x – 3)                                   (ii) x² – 2x = (–2) (3 – x)
(iii) (x – 2)(x + 1) = (x – 1)(x + 3)           (iv) (x – 3)(2x +1) = x(x + 5)
(v) (2x – 1)(x – 3) = (x + 5)(x – 1)          (vi) x² + 3x + 1 = (x – 2)²
(vii) (x + 2)³ = 2x (x² – 1)                         (viii) x³ – 4x² – x + 1 = (x – 2)³

Answer:

 (i) (x + 1)² = 2(x – 3) ⇒x² + 2x + 1 = 2x – 6 ⇒ x² + 7 = 0

 It is of the form ax² + bx +c = 0.

Hence, the given equation is a quadratic equation.

 (ii) x² – 2x = (–2) (3 – x) ⇒ x² – 2x = –6 + 2x ⇒ x² – 4x + 6 = 0

It is of the form ax² + bx + c = 0

Hence, the given equation is a quadratic equation.

(iii) (x – 2) (x + 1) = (x – 1) (x + 3) ⇒ x² – x – 2 = x² + 2x – 3 ⇒ 3x – 1 = 0

 It is not of the form ax² + bx + c = 0.

Hence, the given equation is not a quadratic equation.

(iv) (x – 3) (2x + 1) = x(x + 5) ⇒ 2x² – 5x – 3 = x² + 5x ⇒ x² – 10x – 3 = 0

It is of the form ax² + bx + c = 0.

Hence, the given equation is a quadratic equation.

(v) (2x −1) (x – 3) = (x + 5) (x – 1) ⇒ 2x² – 7x + 3 = x² + 4x – 5 ⇒ x² −11x + 8 = 0, it is of the form ax² + bx + c = 0.

Hence, the given equation is a quadratic equation.

(vi) x² + 3x + 1 = (x – 2)² ⇒ x² + 3x + 1 = x² + 4 – 4x ⇒ 7x – 3 = 0

It is not of the form ax² + bx + c = 0.

Hence, the given equation is not a quadratic equation.

(vii) (x + 2)³ = 2x (x² – 1) ⇒ x³ + 8 + 6x² + 12x = 2x³ – 2x ⇒ x³ – 14x – 6x² – 8 = 0 . It is not of the form ax² + bx + c = 0.

Hence, the given equation is not a quadratic equation.

(viii) x³ – 4x³ – x + 1 = (x – 2)³ ⇒ x³ – 4x² – x + 1 = x³ – 8 – 6x² + 12x ⇒ 2x² – 13x + 9 = 0

It is of the form ax² + bx + c = 0.

Hence, the given equation is a quadratic equation.

Question 8:

ABCD is a cyclic quadrilateral finds the angles of the cyclic quadrilateral.

 

Answer:

We know that the sum of the measures of opposite angles in a cyclic quadrilateral is 180°.

Therefore, ∠A + ∠C = 180

4y + 20 − 4x = 180

− 4x + 4y = 160

x − y = − 40 (i)

Also, ∠B + ∠D = 180

3y − 5 − 7x + 5 = 180

− 7x + 3y = 180 (ii)

Multiplying equation (i) by 3, we obtain

3x − 3y = − 120 (iii)

Adding equations (ii) and (iii), we obtain

− 7x + 3x = 180 − 120

− 4x = 60

x = −15

By using equation (i), we obtain

x − y = − 40

−15 − y = − 40

y = −15 + 40 = 25

∠A = 4y + 20 = 4(25) + 20 = 120°

∠B = 3y − 5 = 3(25) − 5 = 70°

∠C = − 4x = − 4(− 15) = 60°

∠D = − 7x + 5 = − 7(−15) + 5 = 110°

Question 7:

Solve the following pair of linear equations.

(i) px + qy = p − q

qx − py = p + q

(ii) ax + by = c

bx + ay = 1 + c

(iii) (x/a) − (y/b) = 0

ax + by = a² + b²

(iv) (a − b) x + (a + b) y = a²− 2ab − b²

(a + b) (x + y) = a² + b²

(v) 152x − 378y = − 74

− 378x + 152y = − 604

Answer:

(i)px + qy = p − q … (1)

qx − py = p + q … (2)

Multiplying equation (1) by p and equation (2) by q, we obtain

p²x + pqy = p² − pq … (3)

q²x − pqy = pq + q² … (4)

Adding equations (3) and (4), we obtain

p²x + q² x = p² + q²

(p² + q²) x = p² + q²

From equation (1), we obtain

p (1) + qy = p − q

qy = − q

y = − 1

(ii)ax + by = c … (1)

bx + ay = 1 + c … (2)

Multiplying equation (1) by a and equation (2) by b, we obtain

a²x + aby = ac … (3)

b²x + aby = b + bc … (4)

Subtracting equation (4) from equation (3),

(a² − b²) x = ac − bc − b

From equation (1), we obtain

ax + by = c

Or, bx − ay = 0 … (1)

ax + by = a² + b² … (2)

Multiplying equation (1) and (2) by b and a respectively, we obtain

b²x − aby = 0 … (3)

a²x + aby = a³ + ab² … (4)

Adding equations (3) and (4), we obtain

b²x + a²x = a³ + ab²

x (b² + a²) = a (a² + b²)

x = a

By using (1), we obtain

b (a) − ay = 0

ab − ay = 0

ay = ab

y = b

(iv) (a − b) x + (a + b) y = a²− 2ab − b² … (1)

(a + b) (x + y) = a² + b²

(a + b) x + (a + b) y = a² + b² … (2)

 Subtracting equation (2) from (1), we obtain

 (a − b) x − (a + b) x = (a² − 2ab − b²) − (a² + b²)

(a − b − a − b) x = − 2ab − 2b²

− 2bx = − 2b (a + b)

x = a + b

Using equation (1), we obtain

(a − b) (a + b) + (a + b) y = a² − 2ab − b²

a² − b² + (a + b) y = a²− 2ab − b²

(a + b) y = − 2ab

(v) 152x − 378y = − 74

76x − 189y = − 37

− 378x + 152y = − 604

− 189x + 76y = − 302 … (2)

Substituting the value of x in equation (2), we obtain

− (189)² y + 189 × 37 + (76)² y = − 302 × 76

189 × 37 + 302 × 76 = (189)² y − (76)² y

6993 + 22952 = (189 − 76) (189 + 76) y

29945 = (113) (265) y

y = 1

From equation (1), we obtain

Question 6:

Draw the graphs of the equations 5x − y = 5 and 3x − y = 3. Determine the coordinates of the vertices of the triangle formed by these lines and the y axis.

Answer:

5x − y = 5

Or, y = 5x − 5

The solution table will be as follows.

3x − y = 3

Or, y = 3x − 3

The solution table will be as follows.

The graphical representation of these lines will be as follows.

It can be observed that the required triangle is SABC formed by these lines and yaxis.

The coordinates of vertices are A (1, 0), B (0, − 3), C (0, − 5).

Question 5:

In a SABC, ∠C = 3 ∠B = 2 (∠A + ∠B). Find the three angles.
Answer:
Given that,
∠C = 3∠B = 2(∠A + ∠B)
3∠B = 2(∠A + ∠B)
3∠B = 2∠A + 2∠B
∠B = 2∠A
2 ∠A − ∠B = 0 … (i)
We know that the sum of the measures of all angles of a triangle is 180°. Therefore,
∠A + ∠B + ∠C = 180°
∠A + ∠B + 3 ∠B = 180°
∠A + 4 ∠B = 180° … (ii)
Multiplying equation (i) by 4, we obtain
8 ∠A − 4 ∠B = 0 … (iii)
Adding equations (ii) and (iii), we obtain
9 ∠A = 180°
∠A = 20°

From equation (ii), we obtain
20° + 4 ∠B = 180°
4 ∠B = 160°
∠B = 40°
∠C = 3 ∠B
= 3 × 40° = 120°
Therefore, ∠A, ∠B, ∠C are 20°, 40°, and 120° respectively.

Question 4:

The students of a class are made to stand in rows. If 3 students are extra in a row, there would be 1 row less. If 3 students are less in a row, there would be 2 rows more. Find the number of students in the class.

Answer:

Let the number of rows be x and number of students in a row be y.

Total students of the class

= Number of rows × Number of students in a row

= xy

Using the information given in the question,

Condition 1

Total number of students = (x − 1) (y + 3)

xy = (x − 1) (y + 3) = xy − y + 3x − 3

3x − y − 3 = 0

3x − y = 3 (i)

Condition 2

Total number of students = (x + 2) (y − 3)

xy = xy + 2y − 3x − 6

3x − 2y = −6 (ii)

Subtracting equation (ii) from (i),

(3x − y) − (3x − 2y) = 3 − (−6)

− y + 2y = 3 + 6

y = 9

By using equation (i), we obtain

3x − 9 = 3

3x = 9 + 3 = 12

x = 4

Number of rows = x = 4

Number of students in a row = y = 9

Number of total students in a class = xy = 4 × 9 = 36

Question 3:

A train covered a certain distance at a uniform speed. If the train would have been 10 km/h faster, it would have taken 2 hours less than the scheduled time. And if the train were slower by 10 km/h; it would have taken 3 hours more than the scheduled time. Find the distance covered by the train.

Answer:

Let the speed of the train be x km/h and the time taken by train to travel the given distance be t hours and the distance to travel was d km. We know that,

Or, d = xt (i)

Using the information given in the question, we obtain

By using equation (i), we obtain

3x − 10t = 30 (iii)

Adding equations (ii) and (iii), we obtain

x = 50

Using equation (ii), we obtain

(−2) × (50) + 10t = 20

−100 + 10t = 20

10t = 120

t = 12 hours

From equation (i), we obtain

Distance to travel = d = xt

= 50 × 12

= 50 × 12

Hence, the distance covered by the train is 600 km.

Question 2:

One says, “Give me a hundred, friend! I shall then become twice as rich as you”. The other replies, “If you give me ten, I shall be six times as rich as you”. Tell me what is the amount of their (respective) capital? [From the Bijaganita of Bhaskara II)

[Hint: x + 100 = 2 (y − 100), y + 10 = 6(x − 10)]

Answer:

Let those friends were having Rs x and y with them.

Using the information given in the question, we obtain

x + 100 = 2(y − 100)

x + 100 = 2y − 200

x − 2y = −300 (i)

And, 6(x − 10) = (y + 10)

6x − 60 = y + 10

6x − y = 70 (ii)

Multiplying equation (ii) by 2, we obtain

12x − 2y = 140 (iii)

Subtracting equation (i) from equation (iii), we obtain

11x = 140 + 300

11x = 440

x = 40

Using this in equation (i), we obtain

40 − 2y = −300

40 + 300 = 2y

2y = 340

y = 170

Therefore, those friends had Rs 40 and Rs 170 with them respectively.

Question 1:

The ages of two friends Ani and Biju differ by 3 years. Ani’s father Dharam is twice as old as Ani and Biju is twice as old as his sister Cathy. The ages of Cathy and Dharam differs by 30 years. Find the ages of Ani and Biju.

Answer:

The difference between the ages of Biju and Ani is 3 years. Either Biju is 3 years older than Ani or Ani is 3 years older than Biju. However, it is obvious that in both cases, Ani’s father’s age will be 30 years more than that of Cathy’s age.
Let the age of Ani and Biju be x and y years respectively.

Therefore, age of Ani’s father, Dharam = 2 × x = 2x years

And age of Biju’s sister Cathy = y/2 years

By using the information given in the question,

Case (I) When Ani is older than Biju by 3 years,

x − y = 3 (i)

2x − (y/2) = 30

4x − y = 60 (ii)

Subtracting (i) from (ii), we obtain

3x = 60 − 3 = 57

x = 57/3 = 19

Therefore, age of Ani = 19 years

And age of Biju = 19 − 3 = 16 years

Case (II) When Biju is older than Ani,

y − x = 3 (i)

2x − (y/2) = 30

4x − y = 60 (ii)

Adding (i) and (ii), we obtain

3x = 63

x = 21

Therefore, age of Ani = 21 years

And age of Biju = 21 + 3 = 24 years

Question 2:
Formulate the following problems as a pair of equations, and hence find their solutions:
(i) Ritu can row downstream 20 km in 2 hours, and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of the current.
(ii) 2 women and 5 men can together finish an embroidery work in 4 days, while 3 women and 6 men can finish it in 3 days. Find the time taken by 1 woman alone to finish the work, and also that taken by 1 man alone.
(iii) Roohi travels 300 km to her home partly by train and partly by bus. She takes 4 hours if she travels 60 km by train and remaining by bus. If she travels 100 km by train and the remaining by bus, she takes 10 minutes longer. Find the speed of the train and the bus separately.

Answer:

(i) Let the speed of Ritu in still water and the speed of stream be x km/h and y km/h respectively.

Speed of Ritu while rowing

Upstream = (x − y) km/h

Downstream = (x + y) km/h

According to question,

2(x + y) = 20

⇒ x + y = 10       (1)

2(x − y) = 4

⇒ x − y = 2          (2)

Adding equation (1) and (2), we obtain

2x = 12 ⇒ x = 6

Putting this in equation (1), we obtain

y = 4

Hence, Ritu’s speed in still water is 6 km/h and the speed of the current is 4 km/h.

(ii)Let the number of days taken by a woman and a man be x and y respectively.

Therefore, work done by a woman in 1 day = 1/x.

Work done by a man in 1 day = 1/y.

According to the question,

By cross-multiplication, we obtain

Hence, number of days taken by a woman = 18

Number of days taken by a man = 36

(iii) Let the speed of train and bus be u km/h and v km/h respectively.

According to the given information,

Multiplying equation (3) by 10, we obtain

600p + 2400q = 40       (5)

Subtracting equation (4) from (5), we obtain

1200q = 15

q = 15/1200 = 1/80  (6)

Substituting in equation (3), we obtain

60p + 3 = 4

60p = 1

p = 1/60

p = 1/u = 1/60 and q = 1/v = 1/80

u = 60 km/h and v = 80 km/h

Hence, speed of train = 60 km/h

Speed of bus = 80 km/h

Question 1:

Solve the following pairs of equations by reducing them to a pair of linear equations:

Answer:

Multiplying equation (1) by 3, we obtain
6p + 9q = 6 (3)
Adding equation (2) and (3), we obtain

By cross-multiplication, we obtain

Putting this value in equation (1), we obtain

(v)

By cross-multiplication method, we obtain

By cross-multiplication method, we obtain

Substituting in equation (3), we obtain

y = 2

Hence, x = 3, y = 2

Substituting in (2), we obtain

Question 4:

Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method:

(i)A part of monthly hostel charges is fixed and the remaining depends on the number of days one has taken food in the mess. When a student A takes food for 20 days she has to pay Rs 1000 as hostel charges whereas a student B, who takes food for 26 days, pays Rs 1180 as hostel charges. Find the fixed charges and the cost of food per day.

(ii)A fraction becomes 1/3 when 1 is subtracted from the numerator and it becomes 1/4 when 8 is added to its denominator. Find the fraction.

(iii)Yash scored 40 marks in a test, getting 3 marks for each right answer and losing 1 mark for each wrong answer. Had 4 marks been awarded for each correct answer and 2 marks been deducted for each incorrect answer, then Yash would have scored 50 marks. How many questions were there in the test?

(iv) Places A and B are 100 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of the two cars?

(v)The area of a rectangle gets reduced by 9 square units, if its length is reduced by 5 units and breadth is increased by 3 units. If we increase the length by 3 units and the breadth by 2 units, the area increases by 67 square units. Find the dimensions of the rectangle.

Answer:

(i)Let x be the fixed charge of the food and y be the charge for food per day.
According to the given information,

x + 20y = 1000   (1)

x + 26y = 1180   (2)

Subtracting equation (1) from equation (2), we obtain

6y = 180

y = 30

Substituting this value in equation (1), we obtain

x + 20 × 30 = 1000

x = 1000 − 600

x = 400

Hence, fixed charge = Rs 400

And charge per day = Rs 30

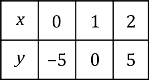
(ii) Let the fraction be x/y.

According to the given information,

Subtracting equation (1) from equation (2), we obtain

x = 5                                   (3)

Putting this value in equation (1), we obtain

15 − y = 13

y = 12

Hence, the fraction is 5/12.

(iii)Let the number of right answers and wrong answers be x and y respectively.

According to the given information,

3x − y = 40       (1)

4x − 2y = 50

⇒ 2x – y = 25   (2)

Subtracting equation (2) from equation (1), we obtain

x = 15 (3)

Substituting this in equation (2), we obtain

30 – y = 25

y = 5

Therefore, number of right answers = 15
And number of wrong answers = 5
Total number of questions = 20

(iv)Let the speed of 1st car and 2nd car be u km/h and v km/h.

Respective speed of both cars while they are travelling in same direction = (u – v) km/h

Respective speed of both cars while they are travelling in opposite directions i.e., travelling towards each other = (u + v) km/h

According to the given information,

5(u – v) = 100

⇒ u – v = 20          ….  (1)

1(u + v) = 100        ….(2)

Adding both the equations, we obtain

2u = 120

u = 60 km/h     …..    (3)

 Substituting this value in equation (2), we obtain v = 40 km/h

Hence, speed of one car = 60 km/h and speed of other car = 40 km/h

(v) Let length and breadth of rectangle be x unit and y unit respectively.

Area = xy

According to the question,

(x – 5) (y + 3) = xy – 9

⇒ 3x – 5y – 6 = 0     (1)

(x + 3) (y + 2) = xy + 67

⇒ 2x + 3y – 61 = 0   (2)

By cross-multiplication method, we obtain

Hence, the length and breadth of the rectangle are 17 units and 9 units respectively.

Question 3:

Solve the following pair of linear equations by the substitution and cross multiplication methods:
8x + 5y = 9
3x + 2y = 4

Answer:

8x + 5y = 9  (i)

3x + 2y = 4  (ii)

From equation (ii), we obtain

Substituting this value in equation (i), we obtain

Question 2:

(i) For which values of a and b will the following pair of linear equations have an infinite number of solutions?

     2x + 3y = 7

    (a – b) x + (a + b) y = 3a + b – 2
(ii) For which value of k will the following pair of linear equations have no solution?
       3x + y = 1
       (2k – 1) x + (k – 1) y = 2k + 1

Answer:

For infinitely many solutions,

Subtracting (1) from (2), we obtain

4b = 4

b = 1

Substituting this in equation (2), we obtain

a − 5 × 1 = 0

a = 5

Hence, a = 5 and b = 1 are the values for which the given equations give infinitely many solutions.

k = 2

Hence, for k = 2, the given equation has no solution.

Question 1:

Which of the following pairs of linear equations has unique solution, no solution or infinitely many solutions? In case there is a unique solution, find it by using cross multiplication method.

(i)   x – 3y – 3 = 0                                               (ii) 2x + y = 5
        3x – 9y – 2 = 0                                                   3x + 2y = 8
(iii) 3x – 5y = 20                                                (iv) x – 3y – 7 = 0
        6x – 10y = 40                                                     3x – 3y – 15 = 0

Answer:

(i)

Therefore, the given sets of lines are parallel to each other. Therefore, they will not intersect each other and thus, there will not be any solution for these equations.

Therefore, they will intersect each other at a unique point and thus, there will be a unique solution for these equations.

By cross-multiplication method,

Therefore, the given sets of lines will be overlapping each other i.e., the lines will be coincident to each other and thus, there are infinite solutions possible for these equations.

Therefore, they will intersect each other at a unique point and thus, there will be a unique solution for these equations.

By cross-multiplication,