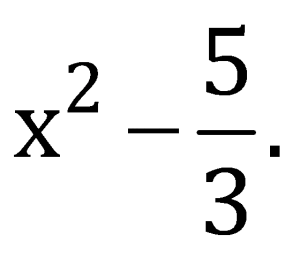CBSE Class X

Question 5:

Give examples of polynomial p(x), g(x), q(x) and r(x), which satisfy the division algorithm and

(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0

Answer:

According to the division algorithm, if p(x) and g(x) are two polynomials with

g(x) ≠ 0, then we can find polynomials q(x) and r(x) such that p(x) = g(x) × q(x) + r(x),

where r(x) = 0 or degree of r(x) < degree of g(x)

Degree of a polynomial is the highest power of the variable in the polynomial.

(i) deg p(x) = deg q(x)

Degree of quotient will be equal to degree of dividend when divisor is constant ( i.e., when any polynomial is divided by a constant).

Let us assume the division 6x² + 2x + 2 by 2.

Here, p(x) = 6x² + 2x + 2

g(x) = 2

q(x) = 3x² + x + 1 and r(x) = 0

Degree of p(x) and q(x) is the same i.e., 2.

Checking for division algorithm,

p(x) = g(x) × q(x) + r(x)

6x² + 2x + 2 = 2 (3x² + x + 1)

= 6x² + 2x + 2

Thus, the division algorithm is satisfied.

(ii) deg q(x) = deg r(x)

Let us assume the division of x³ + x by x²,

Here, p(x) = x³ + x

g(x) = x²

^{q(x) = x and r(x) = x}

^{Clearly, the degree of q(x) and r(x) is the same i.e., 1.}

Checking for division algorithm,
p(x) = g(x) × q(x) + r(x)

x³ + x = (x² ) × x + x
x³ + x = x³ + x

Thus, the division algorithm is satisfied.

(iii) deg r(x) = 0

Degree of remainder will be 0 when remainder comes to a constant.

Let us assume the division of x³ + 1by x².

Here, p(x) = x³ + 1

g(x) = x²

q(x) = x and r(x) = 1

Clearly, the degree of r(x) is 0.

Checking for division algorithm,

p(x) = g(x) × q(x) + r(x)

x³ + 1 = (x² ) × x + 1
x³ + 1 = x³ + 1
Thus, the division algorithm is satisfied.

Question 4:

On dividing x³ – 3x² + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and –2x + 4, respectively. Find g(x).

Answer:

p(x) = x³ − 3x² + x + 2 (Dividend)

g(x) = ? (Divisor)
Quotient = (x − 2)
Remainder = (− 2x + 4)
Dividend = Divisor × Quotient + Remainder

x³ – 3x² +x + 2 = g(x) × (x – 2) + (−2x + 4)

x³ – 3x² + x + 2 + 2x – 4 = g(x) (x – 2)

x³ – 3x² +3x – 2 = g(x) (x – 2)

g(x) is the quotient when we divide (x³ – 3x² +3x – 2) by (x – 2)

∴ g(x) = (x² – x + 1)

Question 3:

Obtain all other zeroes of 3x⁴ + 6x³ – 2x² – 10x – 5, if two of its zeroes are 

Answer:

p(x) = 3x⁴ + 6x³ – 2x² – 10x – 5

Since the two zeroes are 

 is a factor of 3x⁴ + 6x³ – 2x² – 10x – 5.

Therefore, we divide the given polynomial by 

We factorize x² + 2x + 1

= (x + 1)²

Therefore, its zero is given by x + 1 = 0

x = −1

As it has the term (x + 1)², therefore, there will be 2 zeroes at x = −1.

Hence, the zeroes of the given polynomial are  , −1 and −1.

Question 2:

Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:

(i) t² – 3, 2t⁴ + 3t³ – 2t² – 9t – 12
(ii) x² + 3x + 1, 3x⁴ + 5x³ – 7x² + 2x + 2
(iii) x³ – 3x + 1, x⁵ – 4x³ + x² + 3x + 1

Answer:

(i) t² – 3, 2t⁴ + 3t³ – 2t² – 9t – 12

    t² – 3 = t² + 0.t – 3

Since the remainder is 0,

Hence, t² – 3 is a factor of 2t⁴ + 3t³ – 2t² – 9t – 12.

(ii) x² + 3x + 1, 3x⁴ + 5x³ – 7x² + 2x + 2

Since the remainder is 0,

Hence, x² + 3x + 1 is a factor of 3x⁴ + 5x³ – 7x² + 2x + 2.

(iii) x³ – 3x + 1, x⁵ – 4x³ + x² + 3x + 1

Since the remainder ≠ 0,

Hence, x³ – 3x + 1 is not a factor of x⁵ – 4x³ + x² + 3x + 1.

Question 1:

Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:

(i) p(x) = x³ – 3x² + 5x – 3,              g(x) = x² – 2
(ii) p(x) = x⁴ – 3x² + 4x + 5,            g(x) = x² + 1 – x
(iii) p(x) = x⁴ – 5x + 6,                        g(x) = 2 – x²

Answer:

Quotient = x − 3

Remainder = 7x − 9

p(x) = x⁴ – 3x² + 4x + 5 = x⁴ + 0.x³ – 3x² + 4x + 5

q(x) = x² + 1 – x = x² – x + 1

Quotient = x² + x − 3
Remainder = 8

(iii) p(x) = x⁴ – 5x + 6 = x⁴ + 0.x² – 5x + 6

      q(x) = 2 – x² = – x² + 2

Quotient = −x² − 2
Remainder = −5x +10

Question 2:

Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.

(i)   1/4, –1           (ii) √2, 1/3          (iii) 0, √5

(iv)  1,1               (v) –1/4, ¼           (vi) 4, 1

Answer:

(i)   1/4, –1

Let the polynomial be ax² + bx + c, and its zeroes be  α and β.

 

If a = 4, then b = -1, c = -4

Therefore, the quadratic polynomial is 4x² − x − 4.

(ii) √2, 1/3

Let the polynomial be ax² + bx + c, and its zeroes be  α and β.

Therefore, the quadratic polynomial is 3x² − 3√2x + 1.

 (iii) 0, √5

Let the polynomial be ax² + bx + c, and its zeroes be  α and β.

Therefore, the quadratic polynomial is x² + √5.

(iv)  1,1

Let the polynomial be ax² + bx + c, and its zeroes be  α and β.

Therefore, the quadratic polynomial is x² – x + 1.

(v) –1/4, ¼

Let the polynomial be ax² + bx + c, and its zeroes be  α and β.

Therefore, the quadratic polynomial is 4x² + x + 1.

(vi) 4 , 1

Let the polynomial be ax² + bx + c.

Therefore, the quadratic polynomial is x² – 4x + 1.

Question 1:

Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.

(i)   x² – 2x – 8      (ii) 4s² – 4s + 1          (iii) 6x² – 3 – 7x
(iv) 4u² + 8u         (v) t² – 15                  (vi) 3x² – x – 4

Answer:

(i) x² – 2x – 8 = (x – 4) (x + 2)

The value of x² – 2x – 8 is zero when x – 4 = 0 or x + 2 = 0 , i.e, when x = 4 or x = -2

Therefore, the zeroes of x² – 2x – 8 are 4 and −2.

Sum of zeroes = 

Product of zeroes 

(ii) 4s² − 4s + 1 = (2s −1)²

The value of 4s² − 4s + 1 is zero when 2s − 1 = 0, i.e., s = 1/2

Therefore, the zeroes of 4s² − 4s + 1 are 1/2 and 1/2.

Sum of zeroes = 

Product of zeroes 

(iii) 6x² – 3 – 7x = 6x² – 7x – 3 = (3x + 1) (2x – 3)

The value of 6x² − 3 − 7x is zero when 3x + 1 = 0 or 2x − 3 = 0, i.e., x = -1/3 or x = 3/2.

Therefore, the zeroes of 6x² − 3 − 7x are -1/3 and 3/2.

(iv) 4u² + 8u = 4u² + 8u + 0

                         = 4u (u + 2)

The value of 4u² + 8u is zero when 4u = 0 or u + 2 = 0, i.e., u = 0 or u = −2

Therefore, the zeroes of 4u² + 8u are 0 and −2.

(v) t² – 15

           = (t – √15) (t + √15)

(vi) 3x² – x – 4

       = (3x – 4) (x + 1)

The value of 3x² − x − 4 is zero when 3x − 4 = 0 or x + 1 = 0, i.e., when x = 4/3 or x = -1.

Therefore, the zeroes of 3x² – x – 4 are 4/3 and -1.

Question 1:

The graphs of y = p(x) are given in following figure, for some polynomials p(x). Find the number of zeroes of p(x), in each case.

Answer:

(i) The number of zeroes is 0 as the graph does not cut the x-axis at any point.

(ii) The number of zeroes is 1 as the graph intersects the x-axis at only 1 point.

(iii) The number of zeroes is 3 as the graph intersects the x-axis at 3 points.

(iv) The number of zeroes is 2 as the graph intersects the x-axis at 2 points.

(v) The number of zeroes is 4 as the graph intersects the x-axis at 4 points.

(vi) The number of zeroes is 3 as the graph intersects the x-axis at 3 points.