CBSE Class XI

Question 4:

Solve 3x + 8 > 2, when

(i) x is an integer (ii) x is a real number

Answer

The given inequality is 3x + 8 > 2.

3x + 8 > 2

⇒ 3x + 8 – 8 > 2 – 8

⇒ 3x > −6

Question 3:

Solve 5x– 3 < 7, when

(i) x is an integer (ii) x is a real number

Answer

The given inequality is 5x– 3 < 7.

−12x > 30

⇒ 5x – 3 + 3 < 7 + 3

⇒ 5x < 10

 

(i) The integers less than 2 are …, –4, –3, –2, –1, 0, 1.

Thus, when x is an integer, the solutions of the given inequality are …, –4, –3, –2, –1, 0, 1.

Hence, in this case, the solution set is {…, –4, –3, –2, –1, 0, 1}.

(ii) When x is a real number, the solutions of the given inequality are given by x < 2,

that is, all real numbers x which are less than 2.

Thus, the solution set of the given inequality is x ∈ (–∞, 2).

Question 2:

Solve –12x > 30, when

(i) x is a natural number (ii) x is an integer

Answer

The given inequality is –12x > 30.

−12x > 30

 

(i) There is no natural number less than (−5/2).

Thus, when x is a natural number, there is no solution of the given inequality.

(ii) The integers less than (−5/2) are …, –5, –4, –3.

Thus, when x is an integer, the solutions of the given inequality are …, –5, –4, –3.

Hence, in this case, the solution set is {…, –5, –4, –3}.

Question 1:

Solve 24x < 100, when (i) x is a natural number (ii) x is an integer

Answer

The given inequality is 24x < 100

24x < 100

 

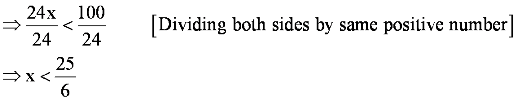
(i) It is evident that 1, 2, 3, and 4 are the only natural numbers less than 25/6.

Thus, when x is a natural number, the solutions of the given inequality are 1, 2, 3, and 4.

Hence, in this case, the solution set is {1, 2, 3, 4}.

(ii) The integers less than 25/6 are … are …–3, –2, –1, 0, 1, 2, 3, 4.

Thus, when x is an integer, the solutions of the given inequality are …–3, –2, –1, 0, 1, 2, 3, 4.

Hence, in this case, the solution set is {…–3, –2, –1, 0, 1, 2, 3, 4}.

Question 20:

Answer

∴ m = 4k, where k is some integer.

Therefore, the least positive integer is 1.

Thus, least positive integral value of m is 4(= 4 ×1).

Question 19:

If (a + ib) (c + id) (e + if) (g + ih) = A + iB, then show that (a² + b²) (c² + d²) (e² + f²) (g² + h²) = A² + B².

Answer

(a + ib) (c + id) (e + if) (g + ih) =A + IB’

∴ |(a + ib) (c + id) (e + if) (g + ih)| = |A + iB|

⇒ |(a + ib) ×|(c + id)| × |(e + if | × |(g + ih)| = |A + iB|   [|z₁z₂| = |z₁||z₂|]

On squaring both sides, we obtain

(a² + b²) (c² + d²) (e² + f²) (g² + h²) = A² + B²

Hence, proved.

Question 18:

Find the number of non-zero integral solutions of the equation |1 –i|^x = 2^x It is given  that, |β| = 1

Answer

|1 – i|^x = 2^x

Thus, 0 is the only integral solution of the given equation. Therefore, the number of non-zero integral solutions of the given equation is 0.

Question 17:

If α and β are different complex numbers with |β| = 1, then find

Answer

Let a = a + ib and β = x + iy

It is given  that, |β| = 1

Question 16:

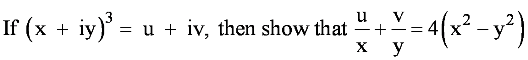
Answer

(x + iy)³ = u + iv

⇒ x³ + (iy)³ + 3 ∙ x ∙ iy(x + iy) = u + iv

⇒ x³ + i³y³ + 3x²yi + 3xy²i² = u + iv

⇒ x³ – iy³ + 3x²­yi− 3xy² = u + iv

⇒ (x³ – 3xy²) + i(3x²y – y³) = u + iv

On equating real and imaginary parts, we obtain

u = x³ – 3xy², v = 3x²y – y³

Question 15:

Answer

Question 14:

Find the real numbers x and y if (x – iy) (3 + 5i) is the conjugate of −6 – 24i.

Answer

Let z = (x – iy) (3 + 5i)

z = 3x + 5xi – 3yi – 5yi² = 3x + 5xi – 3yi + 5y = (3x + 5y) + i(5x – 3y)

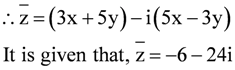
∴ (3x + 5y) – i(5x – 3y) = −6 – 24i

Equating real and imaginary parts, we obtain

3x + 5y = −6                     ….(i)

5x – 3y = 24                      ….(ii)

Multiplying equation (i) by 3 and equation (ii) by 5 and then adding them, we obtain 9x + 15y = −18

Putting the value of x in equation (i), we obtain

3(3) + 5y = −6

⇒ 5y = −6 – 9 = −15

⇒ y = −3

Thus, the values of x and y are 3 and −3 respectively.

Question 13:

Answer

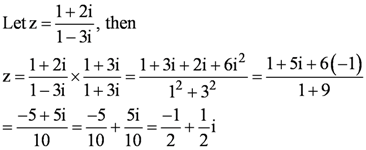
Let z = r cos θ + ir sin θ

i.e., r cos θ = −1/2 and r sin θ = 1/2

On squaring and adding, we obtain

Therefore, the modulus and argument of the given complex number are 1/√2 and 3π/4 respectively.

Question 12:

Let z₁ = 2 – i, z₂ = −2 + i. Find

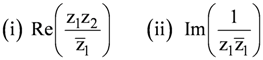
Answer

z₁ = 2 – i, z₂ = −2 + i

(i) z₁z₂ = (2 – i) (−2 + i) = −4 + 2i + 2i – i² = −4 + 4i – (−1) = −3 + 4i

Question 11:

Answer

Question 10:

Answer

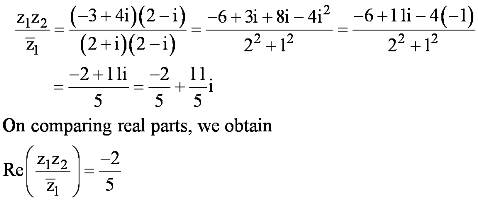
Question 9 :

Solve the equation 21x² – 28x + 10 = 0

Answer

The given quadratic equation is 21x² – 28x + 10 = 0

On comparing the given equation with ax² + bx + c = 0, we obtain

a = 21, b = −28, and c = 10

Therefore, the discriminant of the given equation is

D = b² – 4ac = (−28)² – 4 × 21 × 10 = 784 – 840 = −56

Therefore, the required solutions are

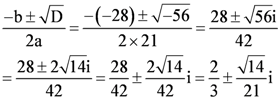
Question 8:

Solve the equation 27x² – 10x + 1 = 0

Answer

The given quadratic equation is 27x² – 10x + 1 = 0

On comparing the given equation with ax² + bx + c = 0, we obtain

a = 27, b = −10, and c = 1

Therefore, the discriminant of the given equation is

D = b² – 4ac =(−10)² – 4 × 27 × 1 = 100 – 108 = −8

Therefore, the required solutions are

Question 7:

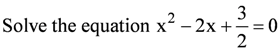
Answer

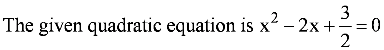
This equation can also be written as 2x³ – 4x + 3 = 0

On comparing this equation with ax² + bx + c = 0, we obtain

a = 2, b = −4, and c = 3

Therefore, the discriminant of the given equation is

D = b² – 4ac = (−4)² – 4 × 2 × 3 = 16 – 24 = −8

Therefore, the required solutions are

Question 6:

Answer

This equation can also be written as 9x² – 12x + 20 = 0

On comparing this equation with ax² + bx + c = 0, we obtain

a = 9, b = −12, and c = 20

Therefore, the discriminant of the given equation is

D = b² – 4ac = (−12)² – 4 × 9 × 20 = 144 – 720 = −576

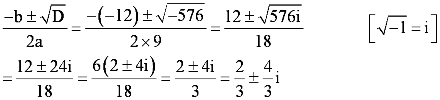
Question 5:

Convert the following in the polar form :

Answer

Let r cos θ = −1 and r sin θ = 1

On squaring and adding, we obtain

r²(cos² θ + sin² θ) = 1 + 1

⇒ r²(cos² θ + sin² θ) = 1 + 1

⇒ r²(cos² θ + sin² θ) = 2

⇒ r² = 2                      [cos² θ + sin² θ = 1]

⇒ r = √2                  [Conventionally, r > 0]

∴ √2 cos θ = −1 and √2 sin θ = 1

Let r cos θ = −1 and r sin θ = 1

On squaring and adding, we obtain

r²(cos² θ + sin² θ)=1 + 1

⇒ r²(cos² θ + sin² θ) = 2

⇒ r² = 2                     [cos² θ + sin² θ = 1]

⇒ r = √2                  [Conventionally, r > 0]

∴ √2 cos θ =−1 and √2 sin θ = 1

This is the required polar form.