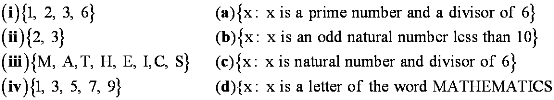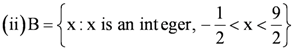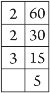CBSE Class XI

Question 9:

Given  the  sets  A  =  {1,  3,  5},  B  =  {2,  4,  6}  and  C  =  {0,  2,  4,  6,  8},  which  of  the following may be considered as universals set (s) for all the three sets A, B and C

(i){0, 1, 2, 3, 4, 5, 6}

(ii) Φ

(iii){0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

(iv){1, 2, 3, 4, 5, 6, 7, 8}

Answer

(i) It can be seen that A ⊂ {0, 1, 2, 3, 4, 5, 6} B ⊂ {0, 1, 2, 3, 4, 5, 6}

However, C ⊄ {0, 1, 2, 3, 4, 5, 6}

Therefore, the set {0, 1, 2, 3, 4, 5, 6} cannot be the universal set for the sets A, B, and C.

(ii) A ⊄ Φ, B ⊄ Φ, C ⊄ Φ

Therefore, Φ cannot be the universal set for the sets A, B, and C.

(iii) A ⊂ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} B ⊂ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

C ⊂ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

Therefore, the set {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,  10} is the universal set for the sets A, B, and C.

(iv) A ⊂ {1, 2, 3, 4, 5, 6, 7, 8} B ⊂ {1, 2, 3, 4, 5, 6, 7, 8}

However, C ⊄ {1, 2, 3, 4, 5, 6, 7, 8}

Therefore, the set  {1,  2,  3,  4,  5,  6,  7,  8} cannot be the universal set for the sets A, B,  and C.

Question 8:

What universal set (s) would you propose for each of the following:

(i) The set of right triangles

(ii) The set of isosceles triangles

Answer

(i) For the set of right triangles, the universal set can be the set of triangles or the set of polygons.

(ii) For the set of isosceles triangles, the universal set can be the set of triangles or the set of polygons or the set of two-dimensional figures.

Question 7:

Write the following intervals in set-builder form:

(i) (−3, 0)

(ii) [6, 12]

(iii) (6, 12]

(iv) [−23, 5)

Answer

(i) (−3, 0) = {x: x ∈ R, −3 < x < 0}

(ii) [6, 12] = {x: x ∈ R, 6 ≤ x ≤ 12}

(iii) (6, 12] ={x: x ∈ R, 6 < x ≤ 12}

(iv) [−23, 5) = {x: x ∈ R, −23 ≤ x < 5}

Question 6 :

Write the following as intervals:

(i) {x: x ∈ R, −4 < x ≤ 6}

(ii) {x: x ∈ R, −12 < x < −10}
(iii) {x: x ∈ R, 0 ≤ x < 7}
(iv) {x: x ∈ R, 3 ≤ x ≤ 4}

Answer

(i) {x: x ∈ R, −4 < x ≤ 6} = (−4, 6]

(ii) {x: x ∈ R, −12 < x < −10} = (−12, −10)
(iii) {x: x ∈ R, 0 ≤ x < 7} = [0, 7)
(iv) {x: x ∈ R, 3 ≤ x ≤ 4} = [3, 4]

Question 5:

How many elements has P(A), if A = Φ?

Answer

We know that if A is a set with m elements i.e., n(A) = m, then n[P(A)] = 2^m. If A = Φ, then n(A) = 0.

∴ n[P(A)] = 2⁰ = 1

Hence, P(A) has one element.

Question 4:

Write down all the subsets of the following sets :

(i){a}

(ii){a, b}

(iii){1, 2, 3}
(iv) Φ

Answer

(i) The subsets of {a} are Φ and {a}.

(ii) The subsets of {a, b} are Φ, {a}, {b}, and {a, b}.

(iii) The subsets of {1, 2, 3} are Φ, {1}, {2}, {3}, {1, 2}, {2, 3}, {1, 3}, and {1, 2, 3}

(iv) The only subset of Φ is Φ.

Question 3 :

Let A= {1, 2, {3, 4,}, 5}. Which of the following statements are incorrect and why?

(i) {3, 4}⊂ A

(ii) {3, 4}}∈ A

(iii) {{3, 4}}⊂ A
(iv) 1∈ A

(v) 1⊂ A

(vi) {1, 2, 5} ⊂ A
(vii) {1, 2, 5} ∈ A
(viii) {1, 2, 3} ⊂ A
(ix) Φ ∈ A

(x) Φ ⊂ A

(xi){Φ} ⊂ A

Answer

A = {1, 2, {3, 4}, 5}

(i) The statement {3, 4} ⊂ A is incorrect because 3 ∈ {3, 4}; however, 3∉A.

(ii) The statement {3, 4} ∈A is correct because {3, 4} is an element of A.

(iii) The statement {{3, 4}} ⊂ A is correct because {3, 4} ∈ {{3, 4}} and {3, 4} ∈ A.

(iv) The statement 1∈A is correct because 1 is an element of A.

(v) The statement  1⊂ A is incorrect because an element of a set can never be a subset of itself.

(vi) The statement {1, 2, 5} ⊂ A is correct because each element of {1, 2, 5} is also an element of A

(vii) The statement {1, 2, 5} ∈ A is incorrect because {1, 2, 5} is not an element of A.

(viii) The statement {1, 2, 3} ⊂ A is incorrect because 3 ∈ {1, 2, 3}; however 3 ∉ A.

(ix) The statement Φ ∈ A is incorrect because Φ is not an element of A.

(x) The statement Φ ⊂ A is correct because Φ is a subset of every set.

(xi) The statement {Φ} ⊂ A is incorrect because Φ∈ {Φ}; however, Φ ∈ A.

Question 2:

Examine whether the following statements are true or false:

(i) {a, b} ⊄ {b, c, a}

(ii) {a, e} ⊂ {x: x is a vowel in the English alphabet}

(iii) {1, 2, 3} ⊂{1, 3, 5}

(iv) {a} ⊂ {a. b, c}

(v) {a} ∈ (a, b, c)

(vi)  {x: x is an even natural number less than  6}  ⊂  {x: x is a natural  number which divides 36}

Answer

(i) False. Each element of {a, b} is also an element of {b, c, a}.

(ii) True. a, e are two vowels of the English alphabet.

(iii) False. 2∈{1, 2, 3}; however, 2∉{1, 3, 5}

(iv) True. Each element of {a} is also an element of {a, b, c.

(v) False. The elements of {a, b, c} are a, b, c. Therefore, {a}⊂{a, b, c}

(vi) True. {x:x is an even natural number less than 6} = {2, 4} {x:x is a natural number which divides 36}= {1, 2, 3, 4, 6, 9, 12, 18, 36}

Question 1:

Make correct statements by filling in the symbols ⊂ or ⊄ in the blank spaces :

(i) {2, 3, 4} … {1, 2, 3, 4, 5}

(ii) {a, b, c} … {b, c, d}

(iii) {x: x is a student of Class XI of your school} … {x: x student of your school}

(iv)  {x: x is a circle in the plane}  …  {x: x is a circle in the same plane with radius 1 unit}

(v) {x: x is a triangle in a plane}…{x: x is a rectangle in the plane}

(vi) {x: x is an equilateral triangle in a plane}… {x: x is a triangle in the same plane}

(vii) {x: x is an even natural number} … {x: x is an integer}

Answer

(i) {2, 3, 4} ⊂ {1, 2, 3, 4, 5}

(ii) {a, b, c} ⊄{b, c, d}

(iii) {x: x is a student of class XI of your school}⊂ {x: x is student of your school}

(iv)  {x:  x is a circle in the plane}  ⊄  {x: x is a circle in  the same plane with  radius 1 unit}

(v) {x: x is a triangle in a plane} ⊄ {x: x is a rectangle in the plane}

(vi) {x: x is an equilateral triangle in a plane}⊂ {x: x in a triangle in the same plane}

Question 6 :

From the sets given below, select equal sets:

A = {2, 4, 8, 12}, B = {1, 2, 3, 4}, C = {4, 8, 12, 14}, D = {3, 1, 4, 2} E = {-1, 1}, F = {0, a}, G = {1, -1}, H = {0, 1}

Answer

A = {2, 4, 8, 12}; B = {1, 2, 3, 4}; C = {4, 8, 12, 14}

D = {3, 1, 4, 2}; E = {-1, 1}; F = {0, a}

G = {1, -1}; A = {0, 1}

It can be seen that

8 ∈ A, 8 ∉ B, 8 ∉ D, 8 ∉ E, 8 ∉ F, 8 ∉ G, 8 ∉

H ⇒ A ≠ B, A ≠ D, A ≠ E, A ≠ F, A ≠ G, A ≠ H Also, 2 ∈ A, 2 ∉ C

∴ A ≠ C

3 ∈ B, 3 ∉ C, 3 ∉ E, 3 ∉ F, 3 ∉ G, 3 ∉ H

∴ B ≠ C, B ≠ E, B ≠ F, B ≠ G, B ≠ H

12 ∈ C, 12 ∉ D, 12 ∉ E, 12 ∉ F, 12 ∉ G, 12 ∉ H

∴ C ≠ D, C ≠ E, C ≠ F, C ≠ G, C ≠ H

4 ∈ D, 4 ∉ E, 4 ∉ F, 4 ∉ G, 4 ∉ H

∴ D ≠ E, D ≠ F, D ≠ G, D ≠ H

Similarly, E ≠ F, E ≠ G, E ≠ H

F ≠ G, F ≠ H, G ≠ H

The order in which the elements of a set are listed is not

significant. ∴ B = D and E = G

Hence, among the given sets, B = D and E = G.

Question 5:

Are the following pair of sets equal? Give reasons.

(i) A = {2, 3}; B = {x: x is solution of x² + 5x + 6 = 0}

(ii) A = {x: x is a letter in the word FOLLOW}; B = {y: y is a letter in the word WOLF}

Answer

(i) A = {2, 3}; B = {x: x is a solution of x² + 5x + 6 = 0}

The equation x² + 5x + 6 = 0 can be solved as:

x(x + 3) + 2(x + 3) = 0

(x + 2)(x + 3) = 0
x = −2 or x = −3

∴A = {2, 3}; B = {−2, −3}
∴A ≠ B

(ii) A = {x: x is a letter in the word FOLLOW} = {F, O, L, W}

B = {y: y is a letter in the word WOLF} = {W, O, L, F}

The order in which the elements of a set are listed is not significant.

∴A = B

Question 4 :

In the following, state whether A = B or not:

(i) A = {a, b, c, d}; B = {d, c, b, a}

(ii) A = {4, 8, 12, 16}; B = {8, 4, 16, 18}

(iii) A = {2, 4, 6, 8, 10}; B = {x: x is positive even integer and x ≤ 10}

(iv) A = {x: x is a multiple of 10}; B = {10, 15, 20, 25, 30….}

Answer

(i) A = {a, b, c, d}; B = {d, c, b, a}

The order in which the elements of a set are listed is not significant.

∴A = B

(ii) A = {4, 8, 12, 16}; B = {8, 4, 16, 18}
It can be seen that 12 ∈ A but 12 ∉ B.
∴A ≠ B.

(iii) A = {2, 4, 6, 8, 10}

B = {x: x is a positive even integer and x ≤ 10} = {2, 4, 6, 8, 10}

∴A = B

(iv) A = {x: x is a multiple of 10}
B = {10, 15, 20, 25, 30 …}

It can be seen that 15 ∈ B but 15 ∉ A.
∴A ≠ B

Question 3 :

State whether each of the following set is finite or infinite:

(i) The set of lines which are parallel to the x-axis

(ii) The set of letters in the English alphabet

(iii) The set of numbers which are multiple of 5

(iv) The set of animals living on the earth

(v) The set of circles passing through the origin (0, 0)

Answer

(i) The  set  of  lines  which  are  parallel  to  the  x-axis  is  an  infinite  set  because  lines parallel to the x-axis are infinite in number.

(ii)The set of letters in the English alphabet is a finite set because it has 26 elements.

(iii)The set of numbers which are multiple of  5 is an infinite set because multiples of  5 are infinite in number.

(iv)The set of animals living on the earth is a finite set because the number of animals living on the earth is finite (although it is quite a big number).

(v) The set of circles passing through the origin  (0,  0) is an infinite set because infinite number of circles can pass through the origin.

Question 2 :

Which of the following sets are finite or infinite

(i) The set of months of a year

(ii) {1, 2, 3 …}

(iii) {1, 2, 3 … 99, 100}

(iv) The set of positive integers greater than 100

(v) The set of prime numbers less than 99

Answer

(i) The set of months of a year is a finite set because it has 12 elements.

(ii) {1, 2, 3 …} is an infinite set as it has infinite number of natural numbers.

(iii) {1,  2,  3  …99,  100} is a finite set because the numbers from  1 to  100 are finite in number.

(iv) The set of positive integers  greater than 100 is an infinite  set  because  positive integers greater than 100 are infinite in number.

(v) The set of prime numbers less than 99 is a finite set because prime numbers less than 99 are finite in number.

Question 1:

Which of the following are examples of the null set

(i) Set of odd natural numbers divisible by 2
(ii) Set of even prime numbers

(iii) {x:x is a natural numbers, x < 5 and x > 7 }

(iv) {y:y is a point common to any two parallel lines}

Answer

(i) A set of odd natural numbers divisible by  2 is a null set because no odd number is divisible by 2.

(ii) A set of even prime numbers is not a null set because 2 is an even prime number.

(iii){x: x is a natural number, x < 5 and x >  7} is a null set because a number cannot be simultaneously less than 5 and greater than 7.

(iv) {y: y is a point common to any two parallel lines} is a null set because parallel lines do not intersect. Hence, they have no common point.

Question 6:

Match  each  of  the  set  on  the  left  in  the  roster  form  with  the  same  set  on  the  right described in set-builder form:

Answer

(i) All  the  elements  of  this  set  are  natural  numbers  as  well  as  the  divisors  of  6.

Therefore, (i) matches with (c).

(ii) It can be seen that 2 and 3 are prime numbers. They are also the divisors of 6. Therefore, (ii) matches with (a).

(iii) All the elements of this set are letters of the word MATHEMATICS. Therefore,  (iii) matches with (d).

(iv) All the elements of this set are odd natural numbers less than  10. Therefore,  (iv) matches with (b).

Question 5:

List all the elements of the following sets :

(i) A = {x: x is an odd natural number}

(iii) C = {x: x is an integer, x² ≤ 4}

(iv) D = {x: x is a letter in the word “LOYAL”}

(v) E = {x: x is a month of a year not having 31 days}

(vi) F = {x: x is a consonant in the English alphabet which proceeds k}.

Answer

(i) A = {x: x is an odd natural number} = {1, 3, 5, 7, 9 …}

 

It can be seen that −1/2 = 0.5 and 9/2 = 4.5

It can be seen that

∴ B ={0, 1, 2, 3, 4}

(iii) C = {x: x is an integer, x² ≤ 4}

It can be seen that

(−1)² = 1 ≤ 4; (−2)² = 4 ≤ 4; (−3)² = 9 > 4

0² = 0 ≤ 4

1² = 1 ≤ 4

2² = 4 ≤ 4

3² = 9 > 4

∴C = {−2, −1, 0, 1, 2}

(iv) D = (x: x is a letter in the word “LOYAL”) = {L, O, Y, A}

(v) E = {x: x is a month of a year not having 31 days} = {February, April, June, September, November}

(vi) F = {x: x is a consonant in the English alphabet which precedes k} = {b, c, d, f, g, h, j }

Question 4:

Write the following sets in the set-builder form:

(i) (3, 6, 9, 12)                   (ii) {2, 4, 8, 16, 32}

(iii) {5, 25, 125, 625}    (iv) {2, 4, 6 …}

Answer

(i) {3, 6, 9, 12} = {x: x = 3n, n∈ N and 1 ≤ n ≤ 4}

(ii) {2, 4, 8, 16, 32}

It can be seen that 2 = 2¹, 4 = 2², 8 = 2³, 16 = 2⁴, and 32 = 2⁵.

∴{2, 4, 8, 16, 32} = {x: x = 2ⁿ, n∈ N and 1 ≤ n ≤ 5}

(iii) {5, 25, 125, 625}

It can be seen that 5 = 5¹, 25 = 5², 125 = 5³, and 625 = 5⁴.

∴ {5, 25, 125, 625} = {x: x = 5ⁿ, n∈N and 1 ≤ n ≤ 4}

(iv) {2, 4, 6 …}

It is a set of all even natural numbers.

∴ {2, 4, 6 …} = {x: x is an even natural number}

(v) {1, 4, 9 … 100}

It can be seen that 1 = 1², 4 = 2², 9 = 3² …100 = 10².

∴ {1, 4, 9… 100} = {x: x = n², n∈N and 1 ≤ n ≤ 10}

Question 3:

Write the following sets in roster form:

(i) A = {x: x is an integer and –3 < x < 7}.

(ii) B = {x: x is a natural number less than 6}.

(iii) C = {x: x is a two-digit natural number such that the sum of its digits is 8}

(iv) D = {x: x is a prime number which is divisor of 60}.

(v) E = The set of all letters in the word TRIGONOMETRY.

(vi) F = The set of all letters in the word BETTER.

Answer

(i) A = {x: x is an integer and –3 < x < 7}

The elements of this set are –2, –1, 0, 1, 2, 3, 4, 5, and 6 only.

Therefore, the given set can be written in roster form as

A = {–2, –1, 0, 1, 2, 3, 4, 5, 6}

(ii) B = {x: x is a natural number less than 6}

The elements of this set are 1, 2, 3, 4, and 5 only.

Therefore, the given set can be written in roster form as

B = {1, 2, 3, 4, 5}

(iii) C = {x: x is a two-digit natural number such that the sum of its digits is 8}

The elements of this set are 17, 26, 35, 44, 53, 62, 71, and 80 only.

Therefore, this set can be written in roster form as

C = {17, 26, 35, 44, 53, 62, 71, 80}

(iv) D = {x: x is a prime number which is a divisor of 60}

∴60 = 2 × 2 × 3 × 5

The elements of this set are 2, 3, and 5 only.

Therefore, this set can be written in roster form as D = {2, 3, 5}.

(v) E = The set of all letters in the word TRIGONOMETRY

There are 12 letters in the word TRIGONOMETRY, out of which letters T, R, and O are repeated.

Therefore, this set can be written in roster form as

E = {T, R, I, G, O, N, M, E, Y}

(vi) F = The set of all letters in the word BETTER

There are 6 letters in the word BETTER, out of which letters E and T are repeated.

Therefore, this set can be written in roster form as F = {B, E, T, R}

Question 2:

Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate symbol ∈ or ∉ in the blank spaces:

(i) 5…A        (ii) 8…A           (iii) 0…A

(iv) 4…A      (v) 2…A          (vi) 10…A

Answer

(i) 5 ∈ A

(ii) 8 ∉ A

(iii) 0 ∉ A

(iv) 4 ∈ A

(v) 2 ∈ A

(vi) 10 ∉ A