CBSE Class XI

Question 4:

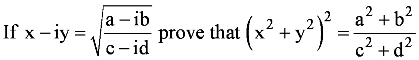
Answer

Question 3:

Answer

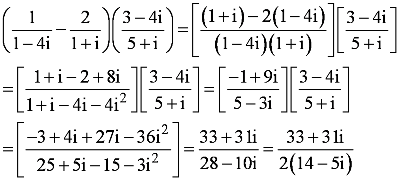
This is the required standard form.

Question 2:

For any two complex numbers z₁ and z₂, prove that

Re (z₁z₂) = Re z₁ Re z₂ – Im z₁ Im z₂

Answer

Let z₁ = x₁ + iy₁ and z₂ = x₂ + iy₂

∴ z₁z₂ = (x₁ + iy₁)(x₂ + iy₂)              

             = x₁(x₂ + iy₂) + iy₁­(x₂ + iy₂)              

             = x₁x₂ +ix₁y₂ + iy₁x₂ + i²y₁y­₂              

             = x₁x₂ + ix₁y₂ + iy₁x₂ + i²y₁y₂              

             = x₁x₂ + ix₁y₂ + iy₁x₂ – y₁y₂              [i² = −1]              

             = (x₁x₂ – y₁y₂) + i(x₁y₂ + y₁x₂)

⇒ Re(z₁z₂) = x₁x₂ – y₁y₂

⇒ Re(z₁z₂) = Rez₁ Rez₂ – Imz₁ Imz₂

Hence, proved.

Question 1:

Answer

Question 10:

Answer

This equation can also be written as √2x² + x + √2 = 0

On comparing this equation with ax² + bx + c = 0, we obtain

a = √2, b = 1, and c = √2

∴ Discriminant (D) = b² – 4ac = 1² – 4 × √2 × √2 = 1 – 8 = −7

Therefore, the required solutions are

Question 9:

Answer

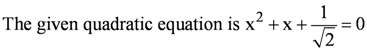
The equation can also the written as √2x² + √2x + 1 = 0

On comparing this equation with ax² + bx + c = 0, we obtain

a = √2, b = √2, and c = 1

∴ Discriminant (D) = b² – 4ac = (√2)² – 4 × (√2) × 1 = 2 – 4√2

Therefore, the required solutions are

Question 8:

Solve the equation √3x² − √2x + 3√3 = 0

Answer

The given quadratic equation is √3x² − √2x + 3√3 = 0

On comparing the given equation with ax² + bx + c = 0, we obtain

a = √3, b = −√2, and c = 3√3

Therefore, the discriminant of the given equation is

D = b² – 4ac = (−√2)² – 4(√3) (3√3) = 2 – 36 = −34

Therefore, the required solutions are

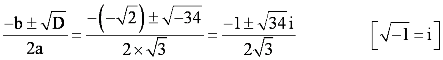
Question 6:

Solve the equation x² – x + 2 = 0

Answer

The given quadratic equation is x² – x + 2 = 0

On comparing the given equation with ax² + bx + c = 0, we obtain

a = 1, b = –1, and c = 2

Therefore, the discriminant of the given equation is

D = b² – 4ac = (–1)2 – 4 × 1 × 2 = 1 – 8 = –7

Therefore, the required solutions are

Question 7:

Solve the equation √2x² + x + √2 = 0

Answer

The given quadratic equation is √2x² + x + √2 = 0

On comparing the given equation with ax² + bx + c = 0, we obtain

a = √2, b = 1, and c = √2

Therefore, the discriminant of the given equation is

D = b² – 4ac = 1² – 4 × √2 × √2 = 1 – 8 = −7

Therefore, the required solutions are

Question 5:

Solve the equation x² + 3x + 5 = 0

Answer

The given quadratic equation is x² + 3x + 5 = 0

On comparing the given equation with ax² + bx + c = 0, we obtain

a = 1, b = 3, and c = 5

Therefore, the discriminant of the given equation is

D = b² – 4ac = 32 – 4 × 1 × 5 =9 – 20 = –11

Therefore, the required solutions are

Question 4:

Solve the equation –x² + x – 2 = 0

Answer

The given quadratic equation is –x² + x – 2 = 0

On comparing the given equation with ax² + bx + c = 0, we obtain

a = –1, b = 1, and c = –2

Therefore, the discriminant of the given equation is

D = b² – 4ac = 1² – 4 × (–1) × (–2) = 1 – 8 = –7

Therefore, the required solutions are

Question 3:

Solve the equation x² + 3x + 9 = 0

Answer

The given quadratic equation is x² + 3x + 9 = 0

On comparing the given equation with ax² + bx + c = 0, we obtain

a = 1, b = 3, and c = 9

Therefore, the discriminant of the given equation is

D = b² – 4ac = 3² – 4 × 1 × 9 = 9 – 36 = –27

Therefore, the required solutions are

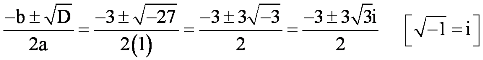
Question 2:

Solve the equation 2x² + x + 1 = 0

Answer

The given quadratic equation is 2x² + x + 1 = 0

On comparing the given equation with ax² + bx + c = 0, we obtain

a = 2, b = 1, and c = 1

Therefore, the discriminant of the given equation is

D = b² – 4ac = 1² – 4 × 2 × 1 = 1 – 8 = –7

Therefore, the required solutions are

Question 1:

Solve the equation x² + 3 = 0

Answer

The given quadratic equation is x² + 3 = 0

On comparing the given equation with ax² + bx + c = 0, we obtain

a = 1, b = 0, and c = 3

Therefore, the discriminant of the given equation is

D = b² – 4ac = 0² – 4 × 1 × 3 = –12

Therefore, the required solutions are

Question 8:

Convert the given complex number in polar form: i

Answer

i

Let r cosθ = 0 and r sin θ = 1

On squaring and adding, we obtain

r² cos² θ + r² sin² θ = 0² + 1²

⇒ r²(cos² θ + sin² θ) = 1

⇒ r² = 1

⇒ r = √1 = 1        [Conventionally, r > 0]

∴ cos θ = 0 and sin θ = 1

∴ θ = π/2

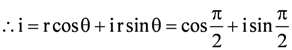
This is the required polar form.

Question 7:

Convert the given complex number in polar form: √3 + i

Answer

√3 + i

Let r cos θ =√3 and r sin θ = 1

On squaring and adding, we obtain

r² cos² θ + r² sin² θ = (√3)² + 1²

⇒ r²(cos² θ + sin² θ) = 3 + 1

⇒ r² = 4

⇒ r = √4 = 2                     [Conventionally, r > 0]

∴ 2 cos θ = √3and 2 sin θ = 1

⇒ cos θ = √3/2 and sin θ = 1/2

∴ θ = π/6                 [As θ lies in the I quadrant]

This is the required polar form.

Question 6:

Convert the given complex number in polar form : −3

Answer

−3

Let r cos θ = −3 and r sin θ = 0

On squaring and adding, we obtain

r² cos² θ + r² sin² θ =(−3)²

⇒ r²(cos² θ + sin² θ) = 9

⇒ r² = 9

⇒ r = √9 = 3        [Conventionally, r >0]

∴ 3 cos θ = −3 and 3 sin θ = 0

⇒ cos θ = −1 and sin θ = 0

∴ θ = π

∴ −3 = r cos θ + i r sin θ = 3 cos π + B sin π = 3(cos π + i sin π)

This is the required polar form.

Question 5:

Convert the given complex number in polar form: – 1 – i

Answer

−1 – i

Let r cos θ = −1 and sin θ = −1

On squaring and adding, we obtain

r² cos² θ + r² sin² θ = (−1)² + (−1)²

⇒ r² (cos² θ + sin²⁺ θ) = 1 + 1

⇒ r² = 2

⇒ r = √2                        [Conventionally, r > 0]

∴ √2 cos θ = −1 and √2 sin θ = −1

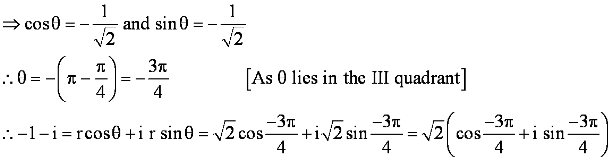
This is the required polar form.

Question 4:

Convert the given complex number in polar form: – 1 + i

Answer

−1 + i

Let r cos θ = −1 and r sin θ = 1

On squaring and adding, we obtain

r² cos² θ + r² sin² θ = (−1)² + 1²

⇒ r²(cos² θ + sin² θ) = 1 + 1

⇒ r² = 2

⇒r = √2                   [Conventionally, r > 0]

∴√2 cos θ = −1 and √2 sin θ = 1

It can be written

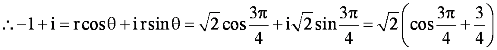
This the required polar form .

Question 3:

Convert the given complex number in polar form: 1 – i

Answer

1 – i

Let r cos θ = 1 and r sin θ = –1

On squaring and adding, we obtain

r² cos² θ + r² sin² θ = 1² + (−1)²

⇒ r²(cos² θ + sin² θ) = 1 + 1

⇒ r² = 2

⇒ r = √2                        [Conventionally, r > 0]

∴ √2 cos θ = 1 and √2 sin θ = −1

⇒ cos θ = 1/√2 and sin θ = −1/√2

∴ θ = −π/4            [As θ lies in the IV quadrant]

This is the required polar form.