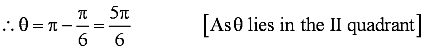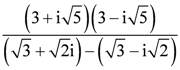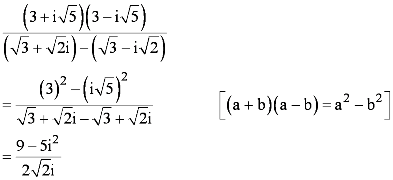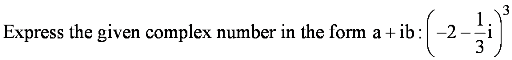CBSE Class XI

Question 2:

Find the modulus and the argument of the complex number z = −√3 + i

Answer

z = −√3 + i

Let r cos θ = −√3 and r sin θ = 1

On squaring and adding, we obtain

r² cos² θ + r² sin² θ =(−√3)² + 1²

⇒ r² = 3 + 1 = 4                           [cos² θ + sin² θ = 1]

⇒ r = √4 = 2                                 [Conventionally, r > 0]

∴ Modulus = 2

∴ 2 cos θ = −√3 and 2 sin θ = 1

⇒ cos θ = −√3/2 and sin θ = 1/2

 

Thus, the modulus and argument of the complex number −√3 + i are 2 and 5π/6 respectively.

Question 1:

Find the modulus and the argument of the complex number z = −1 – i√3

Answer

z = −1 – i√3

Let r cos θ = −1 and r sin θ = −√3

On squaring and adding, we obtain

(r cos θ)² + (r sin θ)² = (−1)² + (−√3)²

⇒ r²(cos² θ + sin² θ) = 1 + 3

⇒ r² = 4                            [cos² θ + sin² θ = 1]

⇒ r = √4 = 2                   [Conventionally, r >0]

∴ Modulus = 2 ∴ 2 cos θ = −1 and 2 sin θ = −√3

⇒ cos θ = −1/2 and sin θ = −√3/2

Since both the values of sin θ and cos θ are negative and sin θ and cos θ are negative in III quadrant,

Thus, the modulus and argument of the complex number −1 – √3i are 2 and −2π/3 respectively.

Question 14:

Express the following expression in the form of a + ib.

Answer

Question 13:

Find the multiplicative inverse of the complex number –i

Answer

Let z = −i

Then,  and |z|² = 1² = 1

Therefore, the multiplicative inverse of –i is given by

Question 12:

Find the multiplicative inverse of the complex number √5 + 3i

Answer

Let z = √5 + 3i

Then,  and |z|² = (√5)² + 3² = 5 + 9 = 14

Therefore, the multiplicative inverse of  √5 + 3i is given  by

Question 11:

Find the multiplicative inverse of the complex number 4 – 3i

Answer

Let z = 4 – 3i

Then,  = 4 + 3i and |z|² = 4² + (−3)² = 16 + 9 = 25

Therefore, the multiplicative inverse of 4 – 3i is given by

Question 10:

Answer

Question 9:

Answer

Question 8:

Express the given complex number in the form a + ib: (1 – i)⁴

Answer

(1 – i)⁴ = [(1 – i)²]²            

              = [1² + i² – 2i]²            

              = [1 – 1 – 2i]²            

              = (−2i)²            

              = (−2i) × (−2i)

              = 4i² = −4          [i² = −1]

Question 7:

Express the given complex number in the form a + ib:

Answer

Question 6:

Answer

Question 5:

Express the given complex number in the form a + ib: (1 – i) – (–1 + i6)

Answer

(1 – i) (−1 + i6) = 1 – i +1 – 6i

                               =2 – 7i

Question 4:

Express the given complex number in the form a + ib: 3(7 + i7) + i(7 + i7)

Answer

3(7 + i7) + i(7 + i7) = 21 + 21i + 7i + 7i²

                                      = 21 +28i + 7 ×(−1)    [∵ i² = −1]

                                      = 14 + 28i

Question 3:

Express the given complex number in the form a + ib: i^–39

Answer

Question 2:

Express the given complex number in the form a + ib: i⁹ + i¹⁹

Answer

i⁹ + i¹⁹ = i^4×2+1 + i^4×4+3            

              =(i⁴)² ∙ i + (i⁴)⁴ ∙ i³              

              = 1 × i +1×(−i)              [i⁴ = 1, i³ = −i]              

              = i + (−i)

              = 0

Question 1:

Answer

Question 24:

Prove the following by using the principle of mathematical induction for all n ∈ N : (2n +7) < (n + 3)²

Answer

Let the given statement be P(n), i.e.,

P(n): (2n +7) < (n + 3)²

It can be observed that P(n) is true for n = 1 since 2.1 + 7 = 9 < (1 + 3)² = 16, which is true.

Let P(k) be true for some positive integer k,

i.e., (2k + 7) < (k + 3)² … (1)

We shall now prove that P(k + 1) is true whenever P(k) is true.

Consider

{2(k +1) + 7} = (2k + 7) + 2

∴{2(k + 1) + 7} = (2k + 7) + 2 < (k + 3)² + 2                 [using (1)]

2(k + 1) + 7 < k² + 6k + 9 + 2

2(k + 1) + 7 < k² + 6k + 11

Now, k² + 6k + 11 < k² +8k + 16

∴2(K + 1) + 7 < (k + 4)²

2(k + 1) + 7<{(k + 1) + 3}²

Thus, P(k + 1) is true whenever P(k) is true.

Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.

Question 23:

Prove the following by using the principle of mathematical induction for all n ∈N : 4ⁿ – 14ⁿ is a multiple of 27.

Answer

Let the given statement be P(n), i.e.,

P(n):41ⁿ – 14ⁿis a multiple of 27.

It can be observed that P(n) is true for n = 1 since 41¹ – 14¹ = 27, which is multiple of 27.

Let P(k) be true for some positive integer k,

41^k – 14^k is a multiple of 27

∴41^k − 14^k = 27m, where m ∈ N … (1)

We shall now prove that P(k + 1) is true whenever P(k) is true.

Consider

41^k+1 – 14^k+1

=41^k ∙ 41 – 14^k ∙ 14

=41(41^k – 14^k + 14^k) – 14^k ∙ 14

=41(41^k – 14^k) + 41∙14^k – 14^k ∙ 14

=41.27m + 14^k(41 – 14)

=41.27m + 27.14^k

=27(41m – 14^k)

= 27 × r, where r = (41m – 14^k) is a natural number

Therefore, 41^k+1 – 14^k+1 is a multiple of 27.

Thus, P(k + 1) is true whenever P(k) is true.

Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.

Question 22:

Prove the following by using the principle of mathematical induction for all n ∈ N: 3^{2n + 2} – 8n – 9 is divisible by 8.

Answer

Let the given statement be P(n), i.e.,

It can be observed that P(n) is true for n = 1 since 3^{2 × 1 + 2} − 8 × 1 – 9 = 64, which is divisible by 8.

Let P(k) be true for some positive integer k,

i.e., 3^{2k + 2} − 8k − 9 is divisible by 8.

∴3^{2k + 2} − 8k − 9 = 8m; where m ∈ N … (1)

We shall now prove that P(k + 1) is true whenever P(k) is true.

Consider

3^2(k+1)+2 – 8(k + 1) – 9

=3^2k+2 ∙ 3² – 8k – 8 – 9

=3²(3^2k+2 – 8k – 9 + 8k + 9) – 8k – 17

= 3²(3^2k+2 – 8k – 9) + 3²(8k + 9) – 8k – 17

= 9.8 m + 9(8k + 9) – 8k – 17

= 9.8m + 72k + 81 – 8k – 17

= 9.8m + 72k + 81 – 8k – 17

= 9.8m + 64k + 64

=8(9m + 8k + 8)

=8r, where r =(9m + 8k + 8) is a natural number

Therefore, 3^2k+2 – 8(k + 1) – 9 is divisible by 8.

Thus, P(k + 1) is true whenever P(k) is true.

Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.

Question 21:

Prove the following by using the principle of mathematical induction for all n ∈N : x²ⁿ – y²ⁿ is divisible by x + y.

Answer

Let the given statement be P(n), i.e.,

P(n): x²ⁿ − y²ⁿ is divisible by x + y.

It can be observed that P(n) is true for n = 1.

This is so because x^{2 × 1} – y^{2 × 1} = x² – y² = (x + y) (x – y) is divisible by (x +y)

Let P(k) be true for some positive integer k, i.e.,

x^2k – y^2k is divisible by x + y.

∴x^2k – y^2k = m (x + y), where m ∈ N … (1)

We shall now prove that P(k + 1) is true whenever P(k) is true.

Consider

x^2(k+1) – y^{2(k + 1)}

=x^2k ∙ x² – y^2k ∙ y²

=x²(x^2k – y^2k + y^2k) – y^2k ∙y²

=x²{m(x + y) + y^2k} – y^2k ∙ y²              [Using (1)]

=m(x + y)x² + y^2k ∙ x² – y^2k ∙ y²

=m(x + y)x² + y^2k (x² – y²)

=m(x + y)x² + y^2k(x + y) (x – y)

=(x + y) {mx² + y^2k(x – y)}, which is factor of (x + y).

Thus, P(k + 1) is true whenever P(k) is true.

Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.