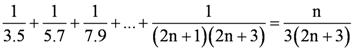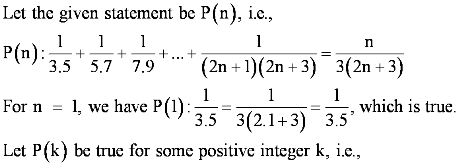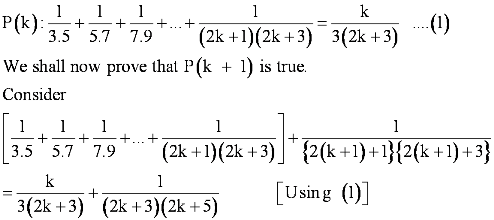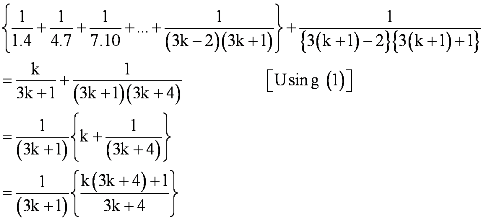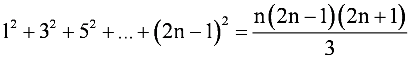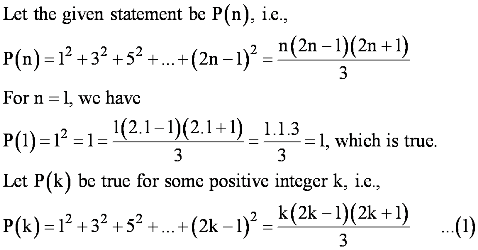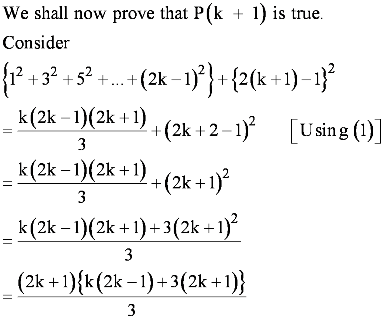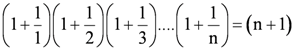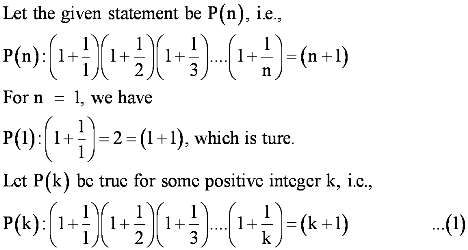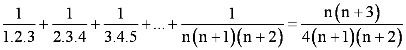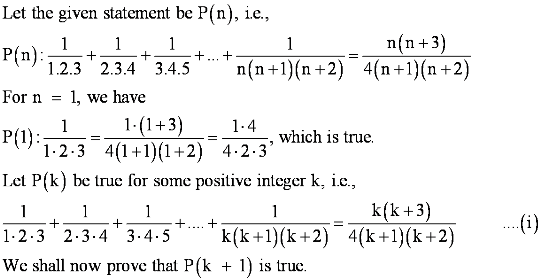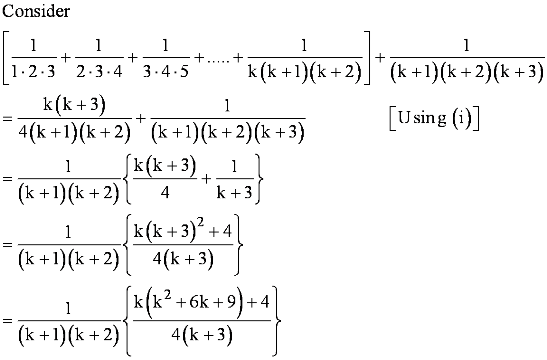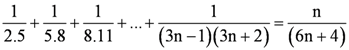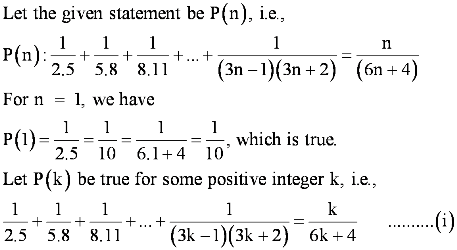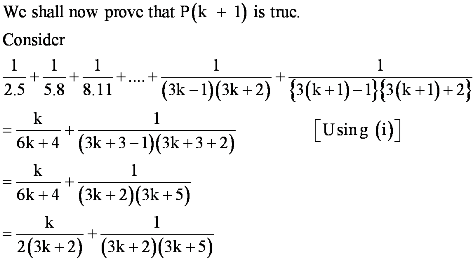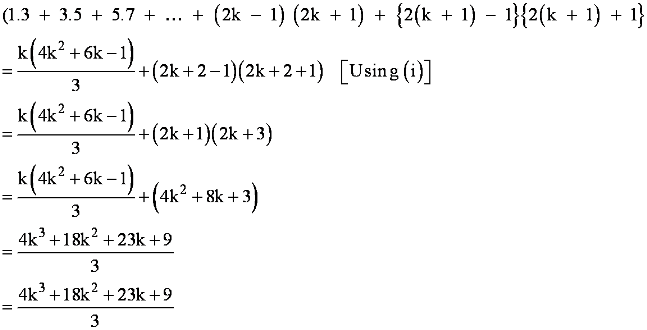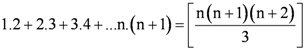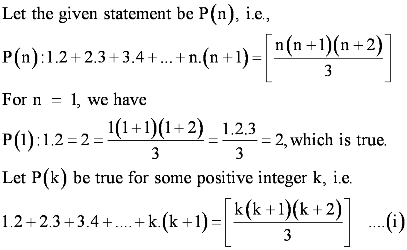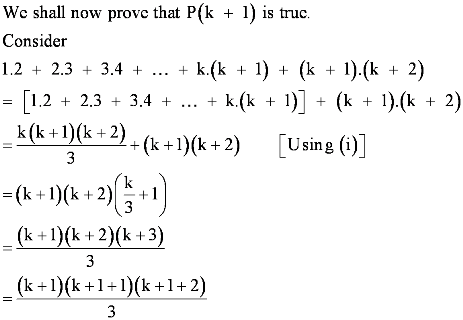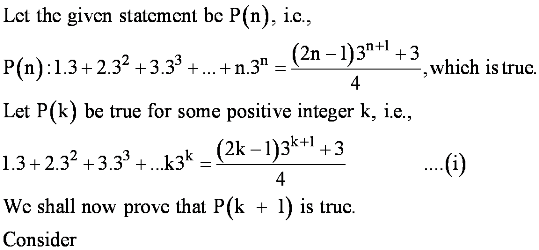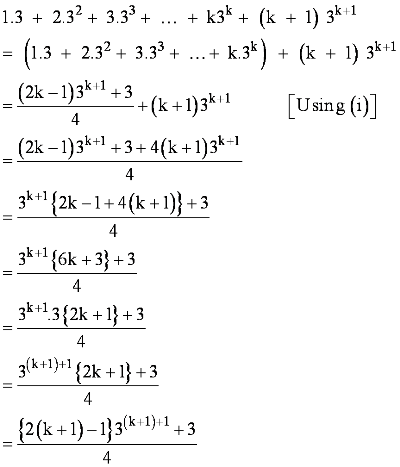Question 20:
Prove the following by using the principle of mathematical induction for all n ∈ N: 102n − 1 + 1 is divisible by 11.
Answer
Let the given statement be P(n), i.e.,
P(n): 102n −1 + 1 is divisible by 11.
It can be observed that P(n) is true for n = 1 since P(1) = 102.1 – 1 + 1 = 11, which is divisible by 11.
Let P(k) be true for some positive integer k,
i.e., 102k − 1 + 1 is divisible by 11.
∴102k −1 + 1 = 11m, where m ∈ N … (1)
We shall now prove that P(k + 1) is true whenever P(k) is true.
Consider
102(k+1)−1 + 1
= 102k+2−1 + 1
=102k+1 + 1
=102(102k−1 + 1 – 1) + 1
=102(102k−1 + 1) – 102 + 1
=102 ∙ 11m – 100 + 1 [Using (1)]
= 100 × 11m – 99
=11(100m – 9)
=11r, where r = (100m – 9) is some natural number
Therefore, 102(k+1) −1 + 1 is divisible by 11.
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.