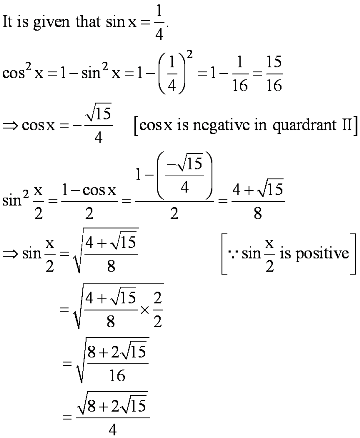
Question 10:
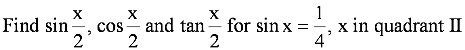
Answer
Here, x is in quadrant II.

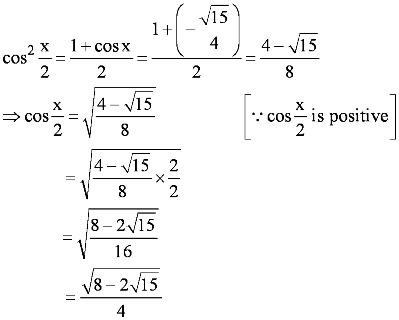
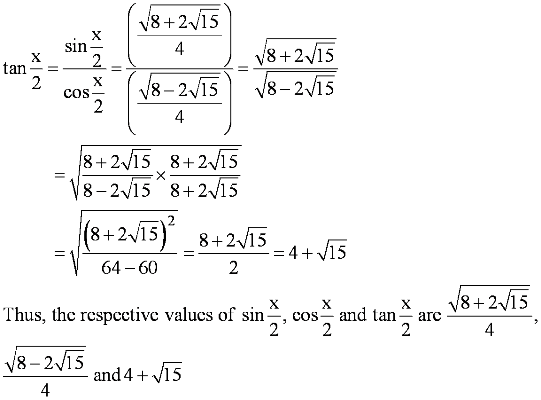
Exams Question Papers General Knowledge Election Directory
Question 10:
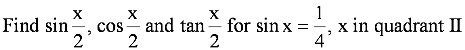
Answer
Here, x is in quadrant II.


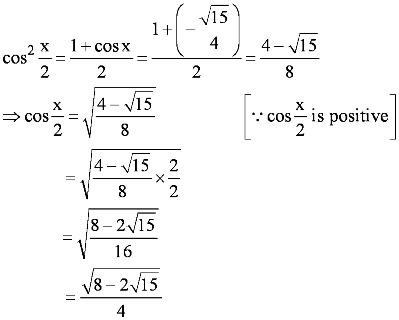
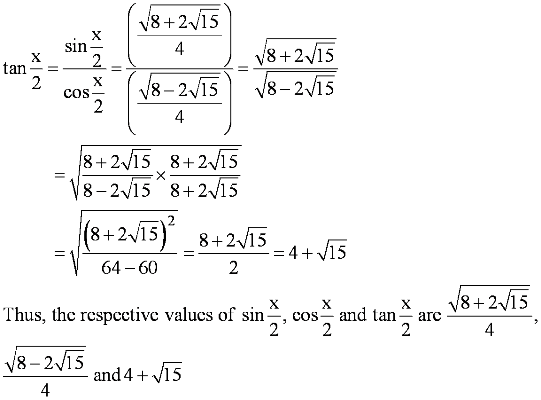
Question 9:
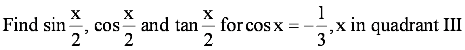
Answer
Here, x is in quadrant III.

It is given that cos x = −1/3.
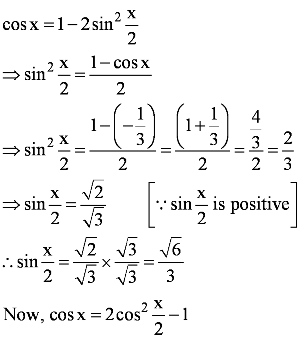

Question 8:
tan x = −4/3, x in quadrant II
Answer
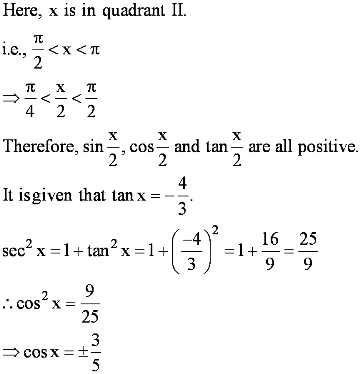
As x is in quadrant II, cosx is negative.
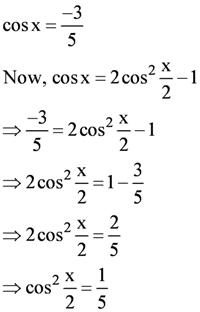

Question 5:
Prove that: sin x + sin 3x + sin 5x + sin 7x = 4 cos x cos 2x sin 4x
Answer
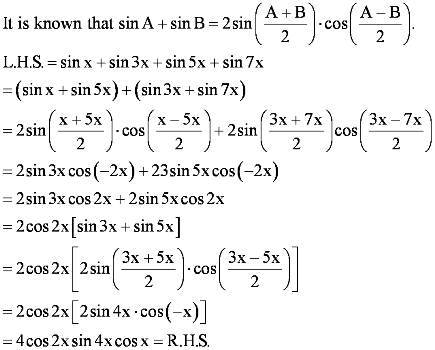
Question 2:
Prove that: (sin 3x + sin x) sin x + (cos 3x − cos x) cos x = 0
Answer
L.H.S. = (sin 3x + sin x) sin x + (cos 3x − cos x) cos x = 0
=sin 3x sin x + sin2 x + cos 3x cos x – cos2 x
=cos 3x cos x + sin 3x sin x – (cos2x – sin2 x)
= cos(3x – x) – cos 2x [cos(A – B) = cos A cos B + sin A sin B]
=cos 2x – cos 2x
= 0
= R.H.S.
Question 9:
Find the general solution of the equation sin x + sin 3x + sin 5x = 0
Answer
sin x + sin 3x + sin 5x = 0
(sin x + sin 5x) + sin 3x = 0
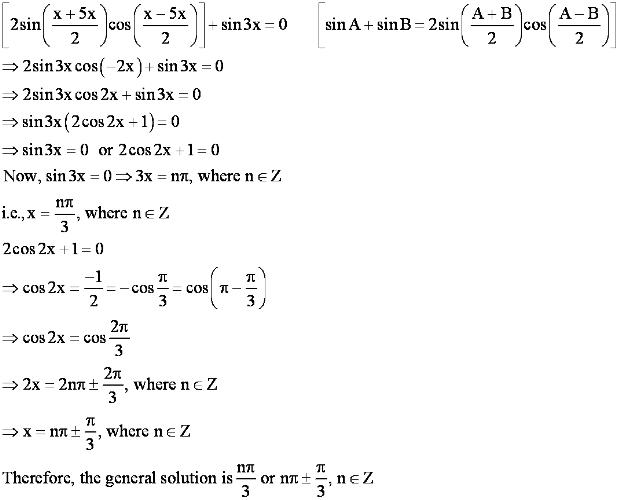
Question 8:
Find the general solution of the equation sec2 2x = 1 – tan 2x
Answer
sec22x = 1- tan 2x
⇒ 1 + tan2 2x= 1 = 1 – tan 2x
⇒ tan2 2x + tan 2x = 0
⇒ tan 2x(tan 2x + 1) = 0
⇒tan 2x = 0 or tan 2x + 1 = 0
Now, tan 2x = 0
⇒ tan 2x = tan 0
⇒ 2x = nπ + 0, where n ∈ Z
⇒ x = nπ/2, where n ∈ Z
tan 2x + 1 = 0

Question 7:
Find the general solution of the equation sin 2x + cos x = 0
Answer

Question 6:
Find the general solution of the equation cos 3x + cos x – cos 2x = 0
Answer
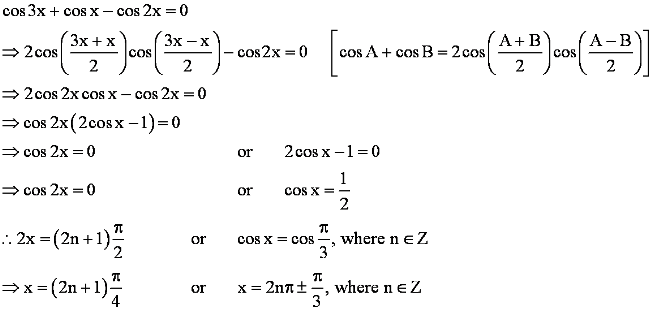
Question 5:
Find the general solution of the equation cos 4x = cos 2x
Answer
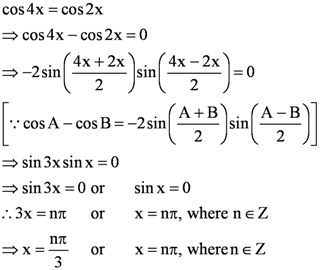
Question 4:
Find the general solution of cosec x = -2
Answer
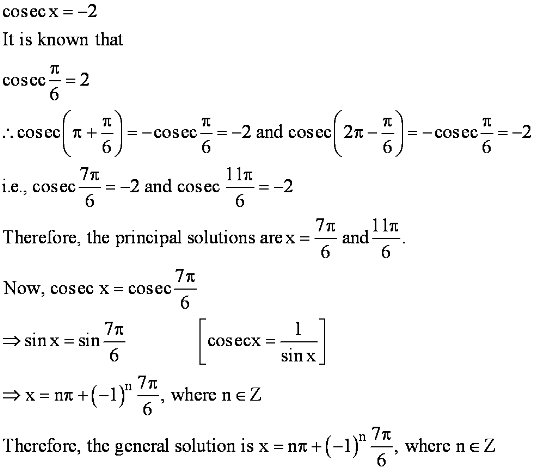
Question 3:
Find the principal and general solutions of the equation cot x = −√3
Answer
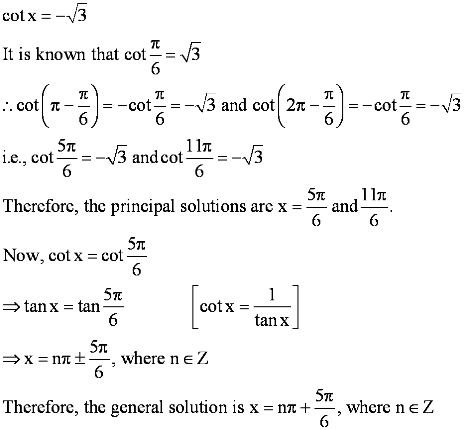
Question 2:
Find the principal and general solutions of the equation sec x = 2
Answer
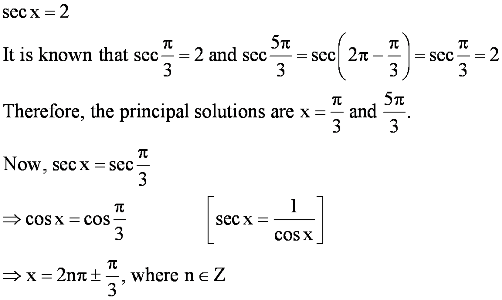
Therefore, the general solution is x = 2nπ ± π/3, where n ∈ Z
Question 1:
Find the principal and general solutions of the equation tan x = √3
Answer

Question 25:
Prove that: cos 6x = 32 cos6 x − 48 cos4 x + 18 cos2 x – 1
Answer
L.H.S. = cos 6x
= cos 3(2x)
= 4 cos3 2x − 3 cos2x [cos 3A = 4 cos3 A − 3 cosA]
= 4 [(2 cos2 x − 1)3 − 3 (2 cos2 x − 1) [cos 2x = 2 cos2 x − 1]
= 4 [(2 cos2 x)3 − (1)3 − 3 (2 cos2 x)2 + 3 (2 cos2 x)] − 6cos2 x + 3
= 4 [8cos6x − 1 − 12 cos4x + 6 cos2x] − 6 cos2x + 3
= 32 cos6x − 4 − 48 cos4x + 24 cos2 x − 6 cos2x + 3
= 32 cos6x − 48 cos4x + 18 cos2x – 1
= R.H.S.