Question 1:
Which of the following relations are functions? Give reasons. If it is a function, determine its domain and range.
(i) {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
(ii) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
(iii) {(1, 3), (1, 5), (2, 5)}
Answer
(i) {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
Since 2, 5, 8, 11, 14, and 17 are the elements of the domain of the given relation having their unique images, this relation is a function.
Here, domain = {2, 5, 8, 11, 14, 17} and range = {1}
(ii) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
Since 2, 4, 6, 8, 10, 12, and 14 are the elements of the domain of the given relation having their unique images, this relation is a function.
Here, domain = {2, 4, 6, 8, 10, 12, 14} and range = {1, 2, 3, 4, 5, 6, 7}
(iii) {(1, 3), (1, 5), (2, 5)}
Since the same first element i.e., 1 corresponds to two different images i.e., 3 and 5, this relation is not a function.
![]()

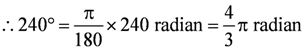

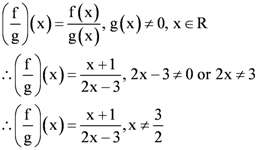
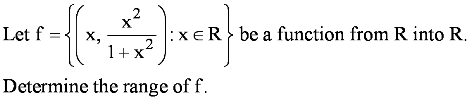

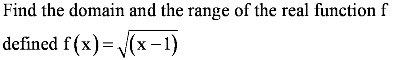
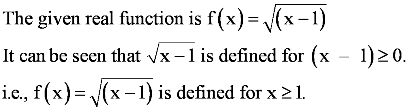
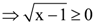
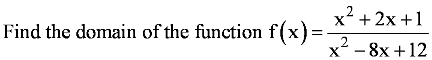
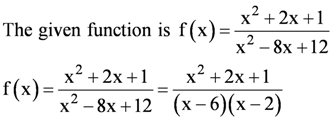
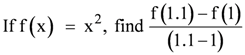


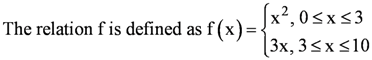
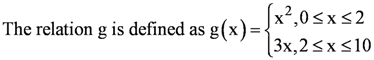
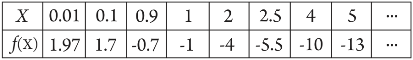
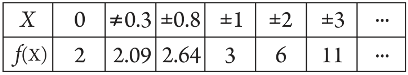
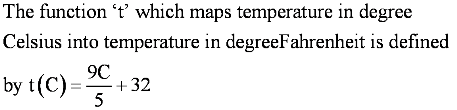


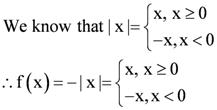
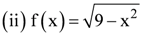
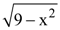 is defined for all real numbers that are greater than or equal to −3 and less than or equal to 3, the domain of f(x) is {x : −3 ≤ x ≤ 3} or [−3, 3].
is defined for all real numbers that are greater than or equal to −3 and less than or equal to 3, the domain of f(x) is {x : −3 ≤ x ≤ 3} or [−3, 3].