CBSE Class XI

Question 7:

Write the relation R = {(x, x³): x is a prime number less than 10} in roster form.

Answer

R = {(x, x³): x is a prime number less than 10}

The prime numbers less than 10 are 2, 3, 5, and 7.

∴ R = {(2, 8), (3, 27), (5, 125), (7, 343)}

Question 6:

Determine the domain and range of the relation R defined by R = {(x, x + 5): x ∈ {0, 1, 2, 3, 4, 5}}.

Answer

R = {(x, x + 5): x ∈ {0, 1, 2, 3, 4, 5}}

∴ R = {(0, 5), (1, 6), (2, 7), (3, 8), (4, 9), (5, 10)}

∴ Domain of R = {0, 1, 2, 3, 4, 5}

Range of R = {5, 6, 7, 8, 9, 10}

Question 5:

Let A = {1, 2, 3, 4, 6}. Let R be the relation on A defined by {(a, b): a, b ∈ A, b is exactly divisible by a}.

(i) Write R in roster form

(ii) Find the domain of R

(iii) Find the range of R.

Answer

A = {1, 2, 3, 4, 6}, R = {(a, b): a, b ∈ A, b is exactly divisible by a}

(i) R = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (6, 6)}

(ii) Domain of R = {1, 2, 3, 4, 6}

(iii) Range of R = {1, 2, 3, 4, 6}

Question 4:

The given figure shows a relationship between the sets P and Q. write this relation

(i) in set-builder form (ii) in roster form.

What is its domain and range?

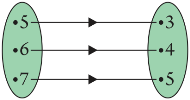
Answer

According to the given figure, P = {5, 6, 7}, Q = {3, 4, 5}

(i) R = {(x, y): y = x − 2; x ∈ P} or R = {(x, y): y = x − 2 for x = 5, 6, 7}

(ii) R = {(5, 3), (6, 4), (7, 5)}

Domain of R = {5, 6, 7}

Range of R = {3, 4, 5}

Question 3:

A = {1, 2, 3, 5} and B = {4, 6, 9}. Define a relation R from A to B by R = {(x, y): the  difference between x and y is odd; x ∈ A, y ∈ B}. Write R in roster form.

Answer

A = {1, 2, 3, 5} and B = {4, 6, 9}

R = {(x, y): the difference between x and y is odd; x ∈ A, y ∈ B}

∴ R = {(1, 4), (1, 6), (2, 9), (3, 4), (3, 6), (5, 4), (5, 6)}

Question 2:

Define a relation R on the set N of natural numbers by R = {(x, y): y = x + 5, x is a natural number less than 4; x, y ∈ N}. Depict this relationship using roster form. Write down the domain and the range.

Answer

R = {(x, y): y = x + 5, x is a natural number less than 4, x, y ∈ N} The natural numbers less than 4 are 1, 2, and 3.

∴ R = {(1, 6), (2, 7), (3, 8)}

The domain of R is the set of all first elements of the ordered pairs in the relation.

∴ Domain of R = {1, 2, 3}

The range of R is the set of all second elements of the ordered pairs in the relation.

∴ Range of R = {6, 7, 8}

Question 1:

Let A = {1, 2, 3, … , 14}. Define a relation R from A to A by R = {(x, y): 3x – y = 0, where x, y ∈ A}. Write down its domain, codomain and range.

Answer

The relation R from A to A is given as R = {(x, y): 3x – y = 0, where x, y ∈ A}

i.e., R = {(x, y): 3x = y, where x, y ∈ A}

∴ R = {(1, 3), (2, 6), (3, 9), (4, 12)}

The domain of R is the set of all first elements of the ordered pairs in the relation.

∴Domain of R = {1, 2, 3, 4}

The whole set A is the codomainof the relation R.

Codomain of R = A = {1, 2, 3, …, 14}

The range of R is the set of all second elements of the ordered pairs in the relation. ∴Range of R = {3, 6, 9, 12}

Question 10:

The Cartesian product A × A has 9 elements among which are found (-1, 0) and (0, 1). Find the set A and the remaining elements of A × A.

Answer

We know that if n(A) = p and n(B) = q, then n(A × B) = pq

∴ n(A × A) = n(A) × n(A)

It is given that n(A × A) = 9

. ∴ n(A) × n(A) = 9

⇒ n(A) = 3

The ordered pairs (−1, 0) and (0, 1) are two of the nine elements of A × A.

We know that A × A = {(a, a): a ∈ A}. Therefore, −1, 0, and 1 are elements of A.

n(A) = 3, it is clear that A = {−1, 0, 1}.

The remaining elements of set A × A are (−1, −1), (−1, 1), (0, −1), (0, 0), (1, −1), (1, 0), and (1, 1)

Question 9:

Let A and B be two sets such that n(A) = 3 and n (B) = 2. If (x, 1), (y, 2), (z, 1) are in A × B, find A and B, where x, y and z are distinct elements.

Answer

It is given that n(A) = 3 and n(B) = 2; and (x, 1), (y, 2), (z, 1) are in A × B.

We know that A = Set of first elements of the ordered pair elements of A × B

B = Set of second elements of the ordered pair elements of A × B.

∴ x, y, and z are the elements of A; and 1 and 2 are the elements of B.

Since n(A) = 3 and n(B) = 2, it is clear that A = {x, y, z} and B = {1, 2}.

Question 8:

Let A = {1, 2} and B = {3, 4}. Write A × B. How many subsets will A × B have? List them.

Answer

A = {1, 2} and B = {3, 4}

∴A × B = {(1, 3), (1, 4), (2, 3), (2, 4)}

⇒ n(A × B) = 4

We know that if C is a set with n(C) = m, then n[P(C)] = 2^m.

Therefore, the set A × B has 2⁴ = 16 subsets. These are

Φ, {(1, 3)}, {(1, 4)}, {(2, 3)}, {(2, 4)}, {(1, 3), (1, 4)}, {(1, 3), (2, 3)}, {(1, 3), (2, 4)}, {(1, 4), (2, 3)}, {(1, 4), (2, 4)}, {(2, 3), (2, 4)}, {(1, 3), (1, 4), (2, 3)}, {(1, 3), (1, 4), (2, 4)}, {(1, 3), (2, 3), (2, 4)}, {(1, 4), (2, 3), (2, 4)}, {(1, 3), (1, 4), (2, 3), (2, 4)}

Question 7:

Let A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8}. Verify that 

(i) A × (B ∩ C) = (A × B) ∩ (A × C)

(ii) A × C is a subset of B × D

Answer

(i) To verify: A × (B ∩ C) = (A × B) ∩ (A × C) We have B ∩ C = {1, 2, 3, 4} ∩ {5, 6} = Φ

∴L.H.S. = A × (B ∩ C) = A × Φ = Φ

A × B = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4)}

A × C = {(1, 5), (1, 6), (2, 5), (2, 6)}

∴ R.H.S. = (A × B) ∩ (A × C) = Φ

∴L.H.S. = R.H.S

Hence, A × (B ∩ C) = (A × B) ∩ (A × C)

(ii) To verify: A × C is a subset of B × D

A × C = {(1, 5), (1, 6), (2, 5), (2, 6)}

B × D = {(1, 5), (1, 6), (1, 7), (1, 8), (2, 5), (2, 6), (2, 7), (2, 8), (3, 5), (3, 6), (3, 7), (3, 8), (4, 5), (4, 6), (4, 7), (4, 8)}

We can observe that all the elements of set A × C are the elements of set B × D.

Therefore, A × C is a subset of B × D.

Question 6:

If A × B = {(a, x), (a, y), (b, x), (b, y)}. Find A and B.

Answer

It is given that A × B = {(a, x), (a, y), (b, x), (b, y)}

We know that the Cartesian product of two non-empty sets P and Q is defined as P × Q = {(p, q): p ∈ P, q ∈ Q}

∴ A is the set of all first elements and B is the set of all second elements. Thus, A = {a, b} and B = {x, y}

Question 5:

If A = {−1, 1}, find A × A × A.

Answer

It is known that for any non-empty set A, A × A × A is defined as A × A × A = {(a, b, c): a, b, c ∈ A}

It is given that A = {−1, 1}

∴ A × A × A = {(−1, −1, −1), (−1, −1, 1), (−1, 1, −1), (−1, 1, 1), (1, −1, −1), (1, −1, 1), (1, 1, −1), (1, 1, 1)}

Question 4:

State whether each of the following statement are true or false. If the statement is false, rewrite the given statement correctly.

(i) If P = {m, n} and Q = {n, m}, then P × Q = {(m, n), (n, m)}.

(ii) If A and B are non-empty sets, then A × B is a non-empty set of ordered pairs (x, y) such that x ∈ A and y ∈ B.

(iii) If A = {1, 2}, B = {3, 4}, then A × (B ∩ Φ) = Φ.

Answer

(i) False

If P = {m, n} and Q = {n, m}, then × Q = {(m, m), (m, n), (n, m), (n, n)}

(ii) True

(iii) True

Question 3:

If G = {7, 8} and H = {5, 4, 2}, find G × H and H × G.

Answer

G = {7, 8} and H = {5, 4, 2}

We know that the Cartesian product P × Q of two non-empty sets P and Q is defined as P × Q = {(p, q): p∈ P, q ∈ Q}

∴G × H = {(7, 5), (7, 4), (7, 2), (8, 5), (8, 4), (8, 2)}

H × G = {(5, 7), (5, 8), (4, 7), (4, 8), (2, 7), (2, 8)}

Question 2:

If the set A has 3 elements and the set B = {3, 4, 5}, then find the number of elements in (A × B)?

Answer

It is given that set A has 3 elements and the elements of set B are 3, 4, and 5.

⇒ Number of elements in set B = 3

Number of elements in (A × B) = (Number of elements in A) × (Number of elements in B) = 3 × 3 = 9

Thus, the number of elements in (A × B) is 9.

Question 1:

Answer

Question 16:

In a survey it was found that 21 people liked product A, 26 liked product B and 29 liked product  C.  If  14  people  liked  products  A  and  B,  12  people  liked  products  C  and  A,  14 people liked products B and C and  8 liked all the three products. Find how many liked product C only.

Answer

Let  A,  B,  and  C  be  the  set  of  people  who  like  product  A,  product  B,  and product  C respectively.

Accordingly, n(A) = 21, n(B) = 26, n(C) = 29, n(A ∩ B) = 14, n(C ∩ A) = 12, n(B ∩ C) = 14, n(A ∩ B ∩ C) = 8

The Venn diagram for the given problem can be drawn as

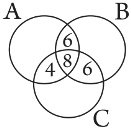
It can be seen that number of people who like product C only is {29 – (4 + 8 + 6)} = 11

Question 15:

In  a  survey  of  60  people,  it  was  found  that  25  people  read  newspaper  H,  26  read newspaper T,  26 read newspaper I,  9 read both H and I,11 read both H and T,  8 read both T and I, 3 read all three newspapers. Find:

(i) the number of people who read at least one of the newspapers.

(ii) the number of people who read exactly one newspaper.

Answer

Let A be the set of people who read newspaper H. Let B be the set of people who read newspaper T. Let C be the set of people who read newspaper I.

Accordingly, n(A) = 25, n(B) = 26, and n(C) = 26 n(A ∩ C) = 9, n(A ∩ B) = 11, and n(B ∩ C) = 8

n(A ∩ B ∩ C) = 3

Let U be the set of people who took part in the survey.

(i) Accordingly, n(A ∪ B ∪ C) = n(A) + n(B) + n(C) − n(A ∩ B) − n(B ∩ C) – n(C ∩ A) + n(A ∩ B ∩ C) = 25 + 26 + 26 −11 − 8 − 9 + 3 = 52

Hence, 52 people read at least one of the newspapers.

(ii) Let a be the number of people who read newspapers H and T only.

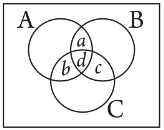
Let b denote the number of people who read newspapers I and H only. Let c denote the number of people who read newspapers T and I only. Let d denote the number of people who read all three newspapers.

Accordingly, d = n(A ∩ B ∩ C) = 3

Now, n(A ∩ B) = a + d

n(B ∩ C) = c + d

n(C ∩ A) = b + d

∴ a + d + c + d + b + d = 11 + 8 + 9 = 28

⇒ a + b + c + d = 28 − 2d = 28 − 6 = 22

Hence, (52 − 22) = 30 people read exactly one newspaper.

Question 14:

In  a  group  of  students  100  students  know  Hindi,  50  know  English  and  25  know  both. Each of the students knows either Hindi or English. How many students are there in the group?

Answer

Let U be the set of all students in the group. Let E be the set of all students who know English. Let H be the set of all students who know Hindi. ∴ H ∪ E = U

Accordingly, n(H) = 100 and n(E) = 50

n(H ∩ E) = 25

n(U) = n(H) + n(E) – n(H ∩ E)

= 100 + 50 – 25

= 125

Hence, there are 125 students in the group.