Graduate Aptitude Test in Engineering 2017

Question Paper Name: Mathematics 5th Feb 2017

Subject Name: Mathematics

Duration : 180

Total Marks: 100

1. Consider the vector space V = {a₀ + a₁x + a₂x² : a_i ∈ ℝ for i = 0, 1, 2} of polynomials of degree at most 2. Let f : V → ℝ be a linear functional such that f(1 + x) = 0, f(1 – x²) = 0 and f(x² – x) = 2. Then f(1 + x + x²) equals _____.

Ans: (1)

2. Let A be a 7 × 7 matrix such that 2A² A⁴ = I, where I is the identity matrix. If A has two distinct eigenvalues and each eigenvalue has geometric multiplicity 3, then the total number of nonzero entries in the Jordan canonical form of A equals ____.

Ans: (8)

3. Let f(z) = (x² + y²) + i2xy and g(z) = 2xy + i(y² – x²) for z = x + iy ∈ ℂ. Then, in the complex plane ℂ,

(A) f is analytic and g is not analytic

(B) f is not analytic and g is analytic

(D) both f and g are analytic

Ans: (B)

4. If 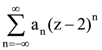is the Laurent series of the function 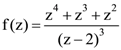for z ∈ ℂ\{2}, then a₋₂ equals _____.

Ans: (48)

5. Let f_n : [0, 1] → ℝ be given by Then the sequence (f_n)

(A) converges uniformly on [0,1]

(B) does NOT converge uniformly on [0, 1] but has a subsequence that converges uniformly on [0, 1]

(D) converges pointwise on [0, 1] but does NOT have a subsequence that converges uniformly on [0, 1]

Ans: (D)

6. Let C : x² + y² = 9 be the circle in ℝ² oriented positively. Then 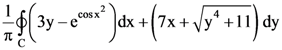equals ____.

Ans: (36)

7. Consider the following statements :

(P) : There exists an unbounded subset of ℝ whose Lebesgue measure is equal to 5.

(Q) If f : ℝ → ℝ is continuous and g : ℝ → ℝ is such that f = g almost everywhere on ℝ, then g must be continuous almost everywhere on ℝ.

Which of the above statements hold TRUE?

(A) Both P and Q

(B) Only P

(D) Neither P nor Q

Ans: (B)

8. If x³y² is an integrating factor of (6y² + a xy) dx + (6xy + bx²) dy = 0, where a, b ∈ ℝ, then

(A) 3a – 5b = 0

(B) 2a – b = 0

(D) 2a + b = 0

Ans: (A)

9. If x(t) and y(t) are the solutions of the system with the initial conditions x(0) = 1 and y(0) = 1, then x(π/2) + y(π/2) equals _____.

Ans: (0)

10. If y = 3e^2x + e^−2x – αx is the solution of the initial value problem where α, β ∈ ℝ, ,then

(A) α = 3 and β = 4

(B) α = 1 and β = 2

(D) α = 1 and β = −2

Ans: (C)

11. Let G be a non-abelian group of order 125. Then the total number of elements in Z(G) = {x ∈ G : g x = x g for all g ∈ G} equals ______.

Ans: (5)

12. Let F₁ and F₂ be subfields of a finite field F consisting of 2⁹ and 2⁶ elements, respectively. Then the total number of elements in F₁ ⋂ F₂ equals ____.

Ans: (8)

13. Consider the normed linear space ℝ² equipped with the norm given by ||(x, y)|| = |x| + |y| and the subspace X = {(x, y) ∈ ℝ² : x = y}. Let f be the linear functional on X given by f(x, y) = 3x. If g(x, y) = αx + βy, α, β ∈ ℝ, is a Hahn-Banach extension of f on ℝ² then α – β equals _____.

Ans: (0)

14. In n ∈ ℤ, define 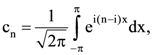where i² = −1. Then equals

(A) cosh(π)

(B) sinh(π)

(D) sinh(2π)

Ans: (D)

15. If the fourth order divided difference of f(x) = αx⁴ + 5x³ + 3x + 2, α ∈ ℝ, at the points 0.1, 0.2, 0.3, 0.4, 0.5 is 5, then α equals ___.

Ans: (5)

16. If the quadrature rule 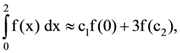where c₁, c₂ ∈ ℝ, is exact for all polynomials of degree ≤ 1, then c₁ + 3c₂ equals _____.

Ans: (1)

17. If u(x, y) = 1 + x + y + f(xy), where f : ℝ² → ℝ is a differentiable function, then u satisfies

(A)

(B)

(C)

(D)

Ans: (C)

18. The partial differential equation 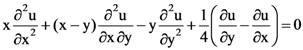is

(A) hyperbolic along the line x + y = 0

(B) elliptic along the line x – y = 0

(D) parabolic along the line x + y = 0

Ans: (D)

19. Let X and Y be topological spaces and let f : X → Y be a continuous surjective function. Which one of the following statements is TRUE?

(A) If X is separable, then Y is separable

(B) If X is first countable, then Y is first countable

(D) If X is regular then Y is regular

Ans: (A)

20. Consider the topology T = {U ⊆ ℤ: ℤ\U is finite or 0 ∉ U} on ℤ. Then, the topological space (ℤ, T) is

(A) compact but NOT connected

(B) connected but NOT compact

(D) neither compact nor connected

Ans: (A)

21. Let F(x) be the distribution function of a random variable X. Consider functions :

G₁(x) = (f(x))³, x ∈ ℝ,

G₂(x) = 1 – (1 – F(x))⁵, x ∈ ℝ.

Which of the above functions are distribution functions?

(A) Neither G₁ nor G₂

(B) Only G₁

(D) Both G₁ and G₂

Ans: (D)

22. Let X₁, X₂, …., X_n (n ≥ 2) be independent and identically distributed random variables with finite variance σ² and let Then the covariance between is

(A) 0

(B) −σ²

(C)

(D)

Ans: (A)

23. Let X₁, X₂, …., X_n(n ≥ 2) be a random sample from a N(μ, σ²) population, where σ² = 144. The smallest n such that the length of the shortest 95% confidence interval for μ will not exceed 10 is _____.

Ans: (23)

24. Consider the linear programming problem (LPP) :

Maximize 4x₁ + 6x₂

Subject to x₁ + x₂ ≤ 8,

2x₁ + 3x₂ ≥ 18,

x₁ ≥ 6, x₂ is unrestricted in sign.

Then the LPP has

(A) no optimal solution

(B) only one basic feasible solution and that is optimal

(D) infinitely many optimal solutions

Ans: (B)

25. For a linear programming problem (LPP) and its dual, which one of the following is NOT TRUE?

(A) The dual of the dual is primal

(B) If the primal LPP has an unbounded objective function, then the dual LPP is infeasible

(D) If the primal LPP has a finite optimal solution, then the dual LPP also has a finite optimal solution

Ans: (C)

26. If U and V are null spaces of 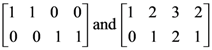, respectively, then the dimension of the subspace U + V equals ______.

Ans: (3)

27. Given two n × n matrices A and B with entries in ℂ, consider the following statements:

(P): If A and B have the same minimal polynomial, then A is similar to B.

(Q) : If A has n distinct eigenvalues, then there exists u ∈ ℂⁿ such that u, Au, ,…, Aⁿ⁻¹u are linearly independent.

Which of the above statements hold TRUE?

(A) Both P and Q

(B) Only P

(D) Neither P nor Q

Ans: (C)

28. Let A = (a_ij) be a 10 × 10 matrix such that a_ij = 1 for i ≠ j and a_ij = α + 1, where α > 0. Let λ and μ be the largest and the smallest eigenvalues of A, respectively. If λ + μ = 24, then α equals ______.

Ans: (7)

29. Let C be the simple, positively oriented circle of radius 2 centered at the origin in the complex plane. Then 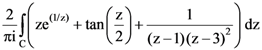equals ______.

Ans: (3)

30. Let Re(z) and Im(z), respectively, denote the real part and the imaginary part of a complex number z. Let T : ℂ ⋃ {∞} → ℂ ⋃ {∞} be the bilinear transformation such that T(6) = 0, T(3 – 3i) = i and T(0) = ∞. Then, the image of D = {z ∈ ℂ : |z – 3| < 3} under the mapping w = T(z) is

(A) {w ∈ ℂ : Im(w) < 0}

(B) {w ∈ ℂ : Re(w) < 0}

(D) {w ∈ ℂ : Re(w) > 0}

Ans: (D)

31. Let (x_n) and (y_n) be two sequences in a complete metric space (X, d) such that and and for all n ∈ ℕ. Then

(A) both (x_n) and (y_n) converge

(B) (x_n) converges but (y_n) need NOT converge

(D) neither (x_n) nor (y_n) converges

Ans: (B)

32. Let f : [0, 1] → ℝ be given by f(x) = 0 if x is rational, and if x is irrational then f(x) = 9ⁿ, where n is the number of zeroes immediately after the decimal point in the decimal representation of x. Then the Lebesgue integral 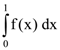equals _____.

Ans: (9)

33. Let f : ℝ² → ℝ be defined by 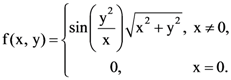Then, at (0, 0),

(A) f is continuous and the directional derivative of f does NOT exist in some direction

(B) f is NOT continuous and the directional derivatives of f exist in all directions

(D) f is differentiable

Ans: (C)

34. Let D be the region in ℝ² bounded by the parabola y² = 2x and the line y = x. Then equals _______.

Ans: (2)

35. Let y₁(x) = x³ and y₂(x) = x²|x| for x ∈ ℝ.

Consider the following statements.

(P) : y₁(x) and y₂(x) are linearly independent solutions of

on ℝ.

(Q) : The Wronskian for all x ∈ ℝ.

Which of the above statement hold TRUE?

(A) Both P and Q

(B) Only P

(D) Neither P nor Q

Ans: (A)

36. Let α and β with α > β be the roots of the indicial equation of at x = −1. Then α − 4β equals _____.

Ans: (2)

37. Let S₉ be the group of all permutations of the set {1, 2, 3, 4, 5, 6, 7, 8, 9}. Then the total number of elements of S₉ that commute with in S₉ equals _______.

Ans: (24)

38. Let ℚ[x] be the ring of polynomials over ℚ. Then the total number of maximal ideals in the quotient ring ℚ[x]/(x⁴ – 1) equals ____.

Ans: (3)

39. Let {e_n : n ∈ ℕ} be an orthonormal basis of a Hilbert space H. Let T : H → H be given by 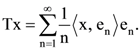For each n ∈ ℕ, define T_n : H → H by 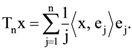Then

(A) ||T_n – T|| → 0 as n → ∞

(B) ||T_n – T|| ↛ 0 as n → ∞ but for each x ∈ H, ||T_nx – Tx|| → 0 as n → ∞

(D) there exist x, y ∈ H such that as n → ∞

Ans: (A)

40. Consider the subspace 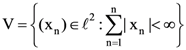of the Hilbert space ℓ² of all square summable real sequences. For n ∈ ℕ, define T_n : V → ℝ by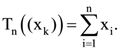

Consider the following statements:

(P): {T_n : n ∈ ℕ} is pointwise bounded on V.

(Q): {T_n : n ∈ ℕ}is uniformly bounded on {x ∈ V : ||x||₂ = 1}.

Which of the above statements hold TRUE?

(A) Both P and Q

(B) Only P

(D) Neither P nor Q

Ans: (B)

41. Let p(x) be the polynomial of degree at most 2 that interpolates the data (−1, 2), (0, 1) and (1, 2). If q(x) is a polynomial of degree at most 3 such that p(x) + q(x) interpolates the data (−1, 2), (0, 1), (1, 2) and (2, 11), then q(3) equals ______.

Ans: (24)

42. Let J be the Jacobi iteration matrix of the linear system

Consider the following statements :

(P): One of the eigenvalues of J lies in the interval [2, 3]

(Q): The Jacobi iteration converges for the above system.

Which of the above statements hold TRUE?

(A) Both P and Q

(B) Only P

(D) Neither P nor Q

Ans: (B)

43. Let u(x, y) be the solution of satisfying the condition u(x, y) = 1 on the circle x² + y² = 1. Then u(2, 2) equals _____.

Ans: (64)

44. Let u(r, θ) be the bounded solution of the following boundary value problem in polar coordinates:

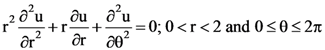
u(2, θ) = cos² θ, 0 ≤ θ ≤ 2π.

Then u(1, π/2) + u(1, π/4) equals

(A) 1

(B) 9/8

(D) 3/8

Ans: (C)

45. Let T_u and T_d denote the usual topology and the discrete topology on ℝ, respectively.

Consider the following three topologies:

T₁ = Usual topology on ℝ² = ℝ × ℝ,

T₂ = Topology generated by the basis {U × V : U ∈ T_d, V ∈ T_u} on ℝ × ℝ,

T₃ = Dictionary order topology on ℝ × ℝ.

Then

(A)

(B)

(C)

(D)

Ans: (D)

46. Let X be a random variable with probability mass function 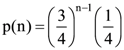for n = 1, 2, ….. . Then E(X – 3 |X > 3) equals _____.

Ans: (4)

47. Let X and Y be independent and identically distributed random variables withi probability mass function p(n) = 2⁻ⁿ, n = 1, 2….. .

Then P(X ≥ 2Y) equals (rounded to 2 decimal places) ____.

Ans: (0.27 to 0.30)

48. Let X₁, X₂, …. be a sequence of independent and identically distributed Poisson random variables with mean 4. Then 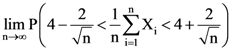equals ____.

Ans: (0.67 to 0.70)

49. Let X and Y be independent and identically distributed exponential random variables with probability density function

The P(max(X, Y) < 2) equals (rounded to 2 decimal places)______.

Ans: (0.73 to 0.77)

50. Let E and F be any two events with P(E) = 0.4, P(F) = 0.3 and P(F\E) = 3 P(F\E^C). Then P(E\F) equals (rounded to 2 decimal places)______.

Ans: (0.65 to 0.68)

51. Let X₁, X₂…, X_m (m ≥ 2) be a random sample from a binomial distribution with parameters n = 1 and p, p ∈ (0, 1), and let

Then a uniformly minimum variance unbiased estimator for p(1 – p) is

(A)

(B)

(C)

(D)

Ans: (A)

52. Let X₁, X₂, …., X₉ be a random sample from a N(0, σ²) population. For teting H₀ : σ² = 2 against H₁ : σ² = 1, the most powerful test rejects H₀ if 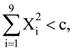where c is to be chosen such that the level of significance is 0.1. Then the power of this test equals ______.

Ans: (0.49 to 0.51)

53. Let X₁, X₂,…, X_n (n ≥ 2) be a random sample from a N(θ, θ) population, where θ > 0, and let Then the maximum likelihood estimator of θ is

(A)

(B)

(C)

(D)

Ans: (D)

54. Consider the following transportation problem. The entries inside the cells denote per unit cost of transportation from the origins to the destinations.

The optimal cost of transportation equals ______.

Ans: (590)

55. Consider the linear programming problem (LPP) :

Maximize kx₁ + 5x₂

subject to x₁ + x₂ ≤ 1,

2x₁ + 3x₂ ≤ 1,

x₁, x₂ ≥ 0.

If x^* = (x₁^*, x₂^*) is an optimal solution of the above LPP with k = 2, then the largest value of k (rounded to 2 decimal places) for which x^* remains optimal equals ______.

Ans: (3.32 to 3.34)

56. The ninth and the tenth of this month are Monday and Tuesday _______.

(A) figuratively

(B) retrospectively

(D) rightfully

Ans: (C)

57. It is _______ to read this year’s textbook ______ the last year’s

(A) easier, than

(B) most easy, than

(D) easiest, from

Ans: (A)

58. A rule states that in order to drink beer, one must be over 18 years old. In a bar, there are 4 people. P is 16 years old, Q is 25 years old, R is drinking milkshake and S is drinking a beer. What must be checked to ensure that the rule is being followed?

(A) Only P’s drink

(B) Only P’s drink and S’s age

(D) Only P’s drink, Q’s drink and S’s age

Ans: (B)

59. Fatima starts from point P, goes North for 3 km, and then East for 4 km to reach point Q. She then turns to face point P and goes 15 km in that direction. She then goes North for 6 km. How far is she from point P, and in which direction should she go to reach point P?

(A) 8 km, East

(B) 12 km, North

(D) 10 km, North

Ans: (A)

60. 500 students are taking one or more courses out of Chemistry, Physics and Mathematics. Registration records indicate course enrolment as follows: Chemistry (329), Physics (186), Mathematics (295), Chemistry and Physics (83), Chemistry and Mathematics (217), and Physics and Mathematics (63). How many students are taking all 3 subjects?

(A) 37

(B) 43

(D) 53

Ans: (D)

61. “If you are looking for a history of India, or for an account of the rise and fall of the British Raj, or for the reason of the cleaving of the subcontinent into two mutually antagonistic parts and the effects this mutilation will have in the respective sections, and ultimately on Asia, you will not find it in these pages; for though I have spent a lifetime in the country. I lived too near the seat of events, and was too intimately associated with the actors, to get the perspective needed for the impartial recording of these matters.”

Which of the following statements best reflects the author’s opinion?

(A) An intimate association does not allow for the necessary perspective.

(B) Matters are recorded with an impartial perspective.

(D) Actors are typically associated with the impartial recording of matters.

Ans: (A)

62. Each of P, Q, R, S, W, X, Y and Z has been married at most once. X and Y are married and have two children P and Q. Z is the grandfather of the daughter S of P. Further, Z and W are married and are parents of R. Which one of the following must necessarily be FALSE?

(A) X is the mother-in-law of R

(B) P and R are not married to each other

(D) Q cannot be married to R

Ans: (D)

63. 1200 men and 500 women can build a bridge in 2 weeks. 900 men and 250 women will take 3 weeks to build the same bridge. How many men will be needed to build the bridge in one week?

(A) 3000

(B) 3300

(D) 3900

Ans: (C)

64. The number of 3-digit numbers such that the digit 1 is never to the immediate right of 2 is

(A) 781

(B) 791

(D) 891

Ans: (C)

65. A contour line joins locations having the same height above the mean sea level. The following is a contour plot of geographical region. Contour lines are shown at 25 m intervals in this plot.

Which of the following is the steepest path leaving from P?

(A) P to Q

(B) P to R

(D) P to T

Ans: (B)

Latest Govt Job & Exam Updates:

Gate 2017 Mathematics Question Paper 5th Feb 2017 PDF Download

View Full List ...