Question 4:
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD
(see the given figure). Show that ∠A > ∠C and ∠B > ∠D.
Answer:
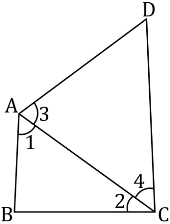
Let us join AC.
In &ABC,
AB < BC (AB is the smallest side of quadrilateral ABCD)
∠2 < ∠1 (Angle opposite to the smaller side is smaller) … (1)
In ∆ADC,
AD < CD (CD is the largest side of quadrilateral ABCD)
∠4 < ∠3 (Angle opposite to the smaller side is smaller) … (2)
On adding equations (1) and (2), we obtain
∠2 + ∠4 < ∠1 + ∠3
∠C < ∠A
∠A > ∠C
Let us join BD.
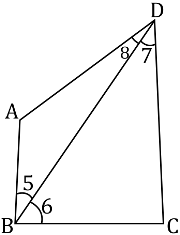
In ∆ABD,
AB < AD (AB is the smallest side of quadrilateral ABCD)
∠8 < ∠5 (Angle opposite to the smaller side is smaller) … (3)
In &BDC,
BC < CD (CD is the largest side of quadrilateral ABCD)
∠7 < ∠6 (Angle opposite to the smaller side is smaller) … (4)
On adding equations (3) and (4), we obtain
∠8 + ∠7 < ∠5 + ∠6
∠D < ∠B
∠B > ∠D
Latest Govt Job & Exam Updates: