Question 12:
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see given figure). Find the sides AB and AC.

Answer:

Let the given circle touch the sides AB and AC of the triangle at point E and F respectively and the length of the line segment AF be x.
In ΔABC,
CF = CD = 6cm (Tangents on the circle from point C)
BE = BD = 8cm (Tangents on the circle from point B)
AE = AF = x (Tangents on the circle from point A)
AB = AE + EB = x + 8
BC = BD + DC = 8 + 6 = 14
CA = CF + FA = 6 + x
2s = AB + BC + CA
= x + 8 + 14 + 6 + x
= 28 + 2x
s = 14 + x
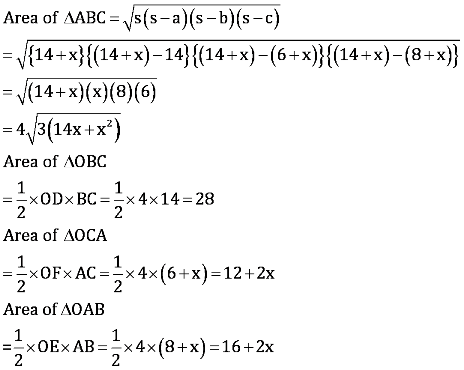
Area of ΔABC = Area of ΔOBC + Area of ΔOCA + Area of ΔOAB

Either x+14 = 0 or x − 7 =0
Therefore, x = −14and 7
However, x = −14 is not possible as the length of the sides will be negative.
Therefore, x = 7
Hence, AB = x + 8 = 7 + 8 = 15 cm
CA = 6 + x = 6 + 7 = 13 cm
Latest Govt Job & Exam Updates: