Question 3:
If tangents PA and PB from a point P to a circle with centre O are inclined to each other an angle of 80º , then ∠POA is equal to
(A) 50º (B) 60º (C) 70º (D) 80º
Answer:
It is given that PA and PB are tangents.
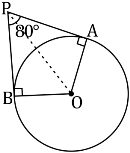
Therefore, the radius drawn to these tangents will be perpendicular to the tangents.
Thus, OA ⊥ PA and OB ⊥ PB
∠OBP = 90º
∠OAP = 90º
In AOBP,
Sum of all interior angles = 360º
∠OAP + ∠APB +∠PBO + ∠BOA = 360º
90º + 80º +90º + BOA = 360º
∠BOA = 100º
In ΔOPB and ΔOPA,
AP = BP (Tangents from a point)
OA = OB (Radii of the circle)
OP = OP (Common side)
Therefore, ΔOPB ≅ ΔOPA (SSS congruence criterion)
A ↔ B, P ↔ P, O ↔ O
And thus, ∠POB = ∠POA
∠POA = 1/2 ∠AOB = 100º/2 = 50º
Hence, alternative (A) is correct.
Latest Govt Job & Exam Updates: