Question 4:
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Answer:
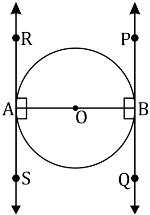
Let AB be a diameter of the circle. Two tangents PQ and RS are drawn at points A and B respectively.
Radius drawn to these tangents will be perpendicular to the tangents.
Thus, OA ⊥ RS and OB ⊥ PQ
∠OAR = 90º
∠OAS = 90º
∠OBP = 90º
∠OBQ = 90º
It can be observed that
∠OAR = ∠OBQ (Alternate interior angles)
∠OAS = ∠OBP (Alternate interior angles)
Since alternate interior angles are equal, lines PQ and RS will be parallel.
Latest Govt Job & Exam Updates: