Question 5:
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Answer:
Let us consider a circle with centre O. Let AB be a tangent which touches the circle at P.
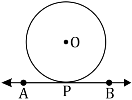
We have to prove that the line perpendicular to AB at P passes through centre O. We shall prove this by contradiction method.
Let us assume that the perpendicular to AB at P does not pass through centre O. Let it pass through another point O’. Join OP and O’P.

As perpendicular to AB at P passes through O’, therefore,
∠O’PB = 90° … (1)
O is the centre of the circle and P is the point of contact. We know the line joining the centre and the point of contact to the tangent of the circle are perpendicular to each other.
∴ ∠OPB = 90° … (2)
Comparing equations (1) and (2), we obtain
∠O’PB = ∠OPB … (3)
From the figure, it can be observed that,
∠O’PB < ∠OPB … (4)
Therefore, ∠O’PB = ∠OPB is not possible. It is only possible, when the line O’P coincides with OP.
Therefore, the perpendicular to AB through P passes through centre O.
Latest Govt Job & Exam Updates: