Question 9:
In the given figure, XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB=90º .

Answer:
Let us join point O to C.
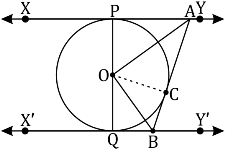
In ΔOPA and ΔOCA,
OP = OC (Radii of the same circle)
AP = AC (Tangents from point A)
AO = AO (Common side)
ΔOPA ≅ ΔOCA (SSS congruence criterion)
Therefore, P ↔ C, A ↔ A, O ↔ O
∠POA = ∠COA … (i)
Similarly, ΔOQB ≅ ΔOCB
∠QOB = ∠COB … (ii)
Since POQ is a diameter of the circle, it is a straight line.
Therefore, ∠POA + ∠COA + ∠COB + ∠QOB = 180º
From equations (i) and (ii), it can be observed that
2∠COA + 2 ∠COB = 180º
∠COA + ∠COB = 90º
∠AOB = 90°
Latest Govt Job & Exam Updates: