Question 5:
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle. Give the justification of the construction.
Answer:
The tangents can be constructed on the given circles as follows.
Step 1
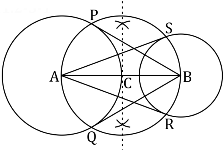
Draw a line segment AB of 8 cm. Taking A and B as centre, draw two circles of 4 cm and 3 cm radius.
Step 2
Bisect the line AB. Let the mid-point of AB be C. Taking C as centre, draw a circle of AC radius which will intersect the circles at points P, Q, R, and S. Join BP, BQ, AS, and AR. These are the required tangents.
Justification
The construction can be justified by proving that AS and AR are the tangents of the circle (whose centre is B and radius is 3 cm) and BP and BQ are the tangents of the circle (whose centre is A and radius is 4 cm). For this, join AP, AQ, BS, and BR.
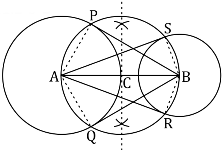
∠ASB is an angle in the semi-circle. We know that an angle in a semi-circle is a right angle.
∴ ∠ASB = 90°
⇒ BS ⊥ AS
Since BS is the radius of the circle, AS has to be a tangent of the circle. Similarly, AR, BP, and BQ are the tangents.
Latest Govt Job & Exam Updates: