Question 1:
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
(i) x2 – 2x – 8 (ii) 4s2 – 4s + 1 (iii) 6x2 – 3 – 7x
(iv) 4u2 + 8u (v) t2 – 15 (vi) 3x2 – x – 4
Answer:
(i) x2 – 2x – 8 = (x – 4) (x + 2)
The value of x2 – 2x – 8 is zero when x – 4 = 0 or x + 2 = 0 , i.e, when x = 4 or x = -2
Therefore, the zeroes of x2 – 2x – 8 are 4 and −2.
Sum of zeroes = 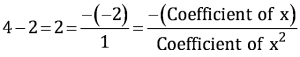
Product of zeroes 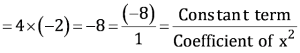
(ii) 4s2 − 4s + 1 = (2s −1)2
The value of 4s2 − 4s + 1 is zero when 2s − 1 = 0, i.e., s = 1/2
Therefore, the zeroes of 4s2 − 4s + 1 are 1/2 and 1/2.
Sum of zeroes = 
Product of zeroes 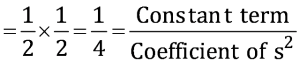
(iii) 6x2 – 3 – 7x = 6x2 – 7x – 3 = (3x + 1) (2x – 3)
The value of 6x2 − 3 − 7x is zero when 3x + 1 = 0 or 2x − 3 = 0, i.e., x = -1/3 or x = 3/2.
Therefore, the zeroes of 6x2 − 3 − 7x are -1/3 and 3/2.

(iv) 4u2 + 8u = 4u2 + 8u + 0
= 4u (u + 2)
The value of 4u2 + 8u is zero when 4u = 0 or u + 2 = 0, i.e., u = 0 or u = −2
Therefore, the zeroes of 4u2 + 8u are 0 and −2.
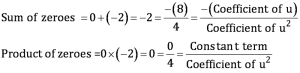
(v) t2 – 15
= (t – √15) (t + √15)

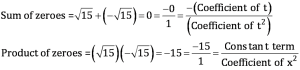
(vi) 3x2 – x – 4
= (3x – 4) (x + 1)
The value of 3x2 − x − 4 is zero when 3x − 4 = 0 or x + 1 = 0, i.e., when x = 4/3 or x = -1.
Therefore, the zeroes of 3x2 – x – 4 are 4/3 and -1.

Latest Govt Job & Exam Updates: