Question 5:
If the polynomial x4 – 6x3 + 16x2 + 10 is divided by another polynomial x2 – 2x + k, the remainder comes out to be x + a, find k and a.
Answer:
By division algorithm,
Dividend = Divisor × Quotient + Remainder
Dividend − Remainder = Divisor × Quotient
x4 – 6x3 + 16x2 – 25x + 10 – x – a = x4 – 6x3 + 16x2 – 26x + 10 – a will be perfectly divisible by x2 – 2x + k.
Let us divide x4 – 6x3 + 16x2 – 26x + 10 – a by x2 – 2x + k
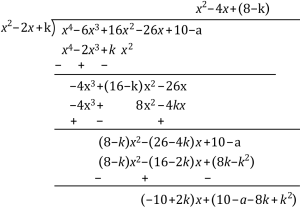
It can be observed that (–10 + 2k) x + (10 – a – 8k + k2) will be 0.
Therefore, (–10 + 2k) = 0 and (10 – a – 8k + k2) = 0
For (–10 + 2k) = 0,
2k = 10
And thus, k = 5
For (10 – a – 8k + k2) = 0
10 – a – 8 × 5 + 25 = 0
10 − a − 40 + 25 = 0
− 5 − a = 0
Therefore, a = −5
Hence, k = 5 and a = −5
Latest Govt Job & Exam Updates: