Question 5:
In the given figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that:


Answer:
(i) Applying Pythagoras theorem in ΔAMD, we obtain
AM2 + MD2 = AD2 … (1)
Applying Pythagoras theorem in ΔAMC, we obtain
AM2 + MC2 = AC2
AM2 + (MD + DC)2 = AC2
(AM2 + MD2) + DC2 + 2MD.DC = AC2
AD2 + DC2 + 2MD.DC = AC2 [Using equation (1)]
Using the result, DC = BC/2, we obtain

(ii) Applying Pythagoras theorem in ΔABM, we obtain
AB2 = AM2 + MB2
= (AD2 − DM2) + MB2
= (AD2 − DM2) + (BD − MD)2
= AD2 − DM2 + BD2 + MD2 − 2BD × MD
= AD2 + BD2 − 2BD × MD
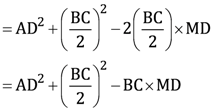
(iii)Applying Pythagoras theorem in ΔABM, we obtain
AM2 + MB2 = AB2 … (1)
Applying Pythagoras theorem in ΔAMC, we obtain
AM2 + MC2 = AC2 … (2)
Adding equations (1) and (2), we obtain
2AM2 + MB2 + MC2 = AB2 + AC2
2AM2 + (BD − DM)2 + (MD + DC)2 = AB2 + AC2
2AM2+BD2 + DM2 − 2BD.DM + MD2 + DC2 + 2MD.DC = AB2 + AC2
2AM2 + 2MD2 + BD2 + DC2 + 2MD (− BD + DC) = AB2 + AC2

Latest Govt Job & Exam Updates: