Question 2:
Find the modulus and the argument of the complex number z = −√3 + i
Answer
z = −√3 + i
Let r cos θ = −√3 and r sin θ = 1
On squaring and adding, we obtain
r2 cos2 θ + r2 sin2 θ =(−√3)2 + 12
⇒ r2 = 3 + 1 = 4 [cos2 θ + sin2 θ = 1]
⇒ r = √4 = 2 [Conventionally, r > 0]
∴ Modulus = 2
∴ 2 cos θ = −√3 and 2 sin θ = 1
⇒ cos θ = −√3/2 and sin θ = 1/2
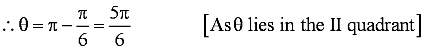
Thus, the modulus and argument of the complex number −√3 + i are 2 and 5π/6 respectively.
Latest Govt Job & Exam Updates: