Question 5:
Find the range of each of the following functions.
(i) f(x) = 2 − 3x, x ∈ R, x > 0.
(ii) f(x) = x2 + 2, x, is a real number.
(iii) f(x) = x, x is a real number
Answer
f(x) = 2 – 3x, x ∈ R, x > 0
The values of f(x) for various values of real numbers x > 0 can be written in the tabular form as
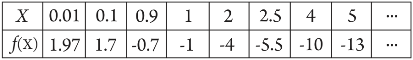
Thus, it can be clearly observed that the range of f is the set of all real numbers less than 2.
i.e., range of f = (−∞, 2)
Alter:
Let x > 0
⇒ 3x > 0
⇒2 – 3x < 2
⇒f(x) < 2
∴ Range of= (−∞, 2)
(ii) f(x) = x2 + 2, x, is a real number
The values of f(x) for various values of real numbers x can be written in the tabular form as
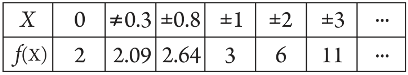
Thus, it can be clearly observed that the range of f is the set of all real numbers greater than 2.
i.e., range of f =[2, ∞)
Alter :
Let x be any real number.
Accordingly,
x2 ≥ 0
⇒ x2 + 2 ≥ 0 + 2
⇒ x2 + 2 ≥ 2
⇒f(x) ≥ 2
∴ Range of f = [2, ∞)
(iii) f(x) = x, x is a real number
It is clear that the range of f is the set of all real numbers.
∴ Range of f = R
Latest Govt Job & Exam Updates: