Question 15:
In a survey of 60 people, it was found that 25 people read newspaper H, 26 read newspaper T, 26 read newspaper I, 9 read both H and I,11 read both H and T, 8 read both T and I, 3 read all three newspapers. Find:
(i) the number of people who read at least one of the newspapers.
(ii) the number of people who read exactly one newspaper.
Answer
Let A be the set of people who read newspaper H. Let B be the set of people who read newspaper T. Let C be the set of people who read newspaper I.
Accordingly, n(A) = 25, n(B) = 26, and n(C) = 26 n(A ∩ C) = 9, n(A ∩ B) = 11, and n(B ∩ C) = 8
n(A ∩ B ∩ C) = 3
Let U be the set of people who took part in the survey.
(i) Accordingly, n(A ∪ B ∪ C) = n(A) + n(B) + n(C) − n(A ∩ B) − n(B ∩ C) – n(C ∩ A) + n(A ∩ B ∩ C) = 25 + 26 + 26 −11 − 8 − 9 + 3 = 52
Hence, 52 people read at least one of the newspapers.
(ii) Let a be the number of people who read newspapers H and T only.
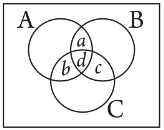
Let b denote the number of people who read newspapers I and H only. Let c denote the number of people who read newspapers T and I only. Let d denote the number of people who read all three newspapers.
Accordingly, d = n(A ∩ B ∩ C) = 3
Now, n(A ∩ B) = a + d
n(B ∩ C) = c + d
n(C ∩ A) = b + d
∴ a + d + c + d + b + d = 11 + 8 + 9 = 28
⇒ a + b + c + d = 28 − 2d = 28 − 6 = 22
Hence, (52 − 22) = 30 people read exactly one newspaper.
Latest Govt Job & Exam Updates: