Question 2:
If the median of the distribution is given below is 28.5, find the values of x and y.
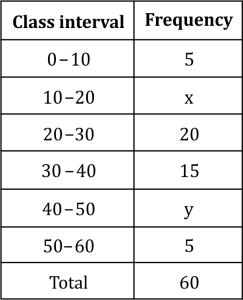
Answer:
The cumulative frequency for the given data is calculated as follows.

From the table, it can be observed that n = 60
45 + x + y = 60
x + y = 15 (1)
Median of the data is given as 28.5 which lies in interval 20 − 30.
Therefore, median class = 20 − 30
Lower limit (l) of median class = 20
Cumulative frequency (cf) of class preceding the median class = 5 + x
Frequency (f) of median class = 20
Class size (h) = 10
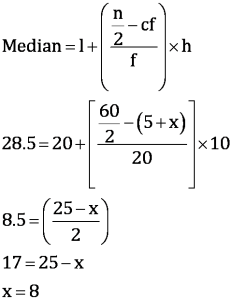
From equation (1),
8 + y = 15
y = 7
Hence, the values of x and y are 8 and 7 respectively
Latest Govt Job & Exam Updates: