Physics
1. A block of mass m attached to a massless spring is performing oscillatory motion of amplitude ‘A’ on a frictionless horizontal plane. If half of the mass of the block breaks off when it is passing through its equilibrium point, the amplitude of oscillation for the remaining system become fA. The value of f is:
(1) 1/√2
(2) 1/2
(3) 1
(4) √2
2. The mass density of a planet of radius R varies with the distance r from its centre as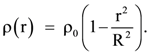 
Then the gravitational field is maximum at:
(1) 
(2) 
(3) r = R
(4) 
3. Two sources of light emit X-rays of wavelength 1 nm and visible light of wavelength 500 nm, respectively. Both the sources emit light of the same power 200 W. The ratio of the number density of photons of X-rays to the number density of photons of the visible light of the given wavelengths is:
(1) 1/500
(2) 1/250
(3) 500
(4) 250
4. If a semiconductor photodiode can detect a photon with a maximum wavelength of 400nm, then its band gap energy is : Planck’s constant h = 6.63 × 10–34s. Speed of light c = 3 × 108 m/s
(1) 1.5 eV
(2) 2.0 eV
(3) 3.1 eV
(4) 1.1 eV
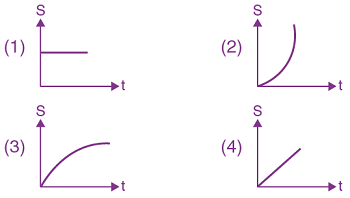
6. A particle is moving unidirectionally on a horizontal plane under the action of a constant power supplying energy source. The displacement (s) – time (t) graph that describes the motion of the particle is (graphs are drawn schematically and are not to scale:
7. Which of the following will NOT be observed when a multimeter (operating in resistance measuring mode) probes connected across a component, are just reversed?
(1) Multimeter shows NO deflection in both cases i.e. before and after reversing the probes if the chosen component is metal wire.
(2) Multimeter shows a deflection, accompanied by a splash of light out of connected component in one direction and NO deflection on reversing the probes if the chosen component is LED.
(3) Multimeter shows an equal deflection in both cases i.e. before and after reversing the probes if the chosen component is resistor.
(4) Multimeter shows NO deflection in both cases i.e. before and after reversing the probes if the chosen component is capacitor.
8. A uniform rod of length ‘l’ is pivoted at one of its ends on a vertical shaft of negligible radius. When the shaft rotates at angular speed ω the rod makes an angle θ with it (see figure). To find θ equate the rate of change of angular momentum (direction going into the paper) 
about the centre of mass (CM) to the torque provided by the horizontal and vertical forces FH and FV about the CM. The value of θ is then such that:
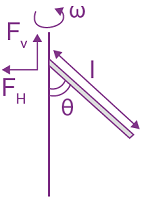
(1) cos θ = 2g/3l ω2
(2) cos θ = 3g/2l ω2
(3) cos θ = g/2l ω2
(4) cos θ = g/I ω2
9. Two resistors 400 Ω and 800 Ω are connected in series across a 6 V battery. The potential difference measured by a voltmeter of 10 k Ω across 400 Ω resistors is close to:
(1) 2.05 V
(2) 2 V
(3) 1.95 V
(4) 1.8 V
10. A block of mass 1.9 kg is at rest at the edge of a table, of height 1 m. A bullet of mass 0.1 kg collides with the block and sticks to it. If the velocity of the bullet is 20 m/s in the horizontal direction just before the collision then the kinetic energy just before the combined system strikes the floor, is [Take g = 10 m/s2 . Assume there is no rotational motion and loss of energy after the collision is negligible.]
(1) 23 J
(2) 21 J
(3) 20 J
(4) 19 J
11. A metallic sphere cools from 50°C to 40°C in 300 s. If atmospheric temperature around is 20°C, then the sphere’s temperature after the next 5 minutes will be close to :
(1) 35°C
(2) 31°C
(3) 33°C
(4) 28°C
12. To raise the temperature of a certain mass of gas by 50°C at a constant pressure, 160 calories of heat is required. When the same mass of gas is cooled by 100°C at constant volume, 240 calories of heat is released. How many degrees of freedom does each molecule of this gas have (assume gas to be ideal)?
(1) 6
(2) 7
(3) 5
(4) 3
13. The radius R of a nucleus of mass number A can be estimated by the formula R = (1.3 × 10–15)A 1/3 m. It follows that the mass density of a nucleus is of the order of: (M = Mneut =1.67 × 10–27 kg)
(1) 1017 kg m−3
(2) 1010 kg m−3
(3) 1024 kg m−3
(4) 103 kg m−3
14. A perfectly diamagnetic sphere has a small spherical cavity at its centre, which is filled with a paramagnetic substance. The whole system is placed in a uniform magnetic field B. Then the field inside the paramagnetic substance is:
(1) much large than 
and parallel to 
(2) zero
(3)
(4) much large than but opposite to
15. Concentric metallic hollow spheres of radii R and 4R hold charges Q1 and Q2 Given that surface charge densities of the concentric spheres are equal, the potential difference V(R) – V(4R) is:
(1) 
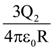
(2) 
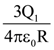
(3) 
(4) 
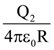
16. The electric field of a plane electromagnetic wave propagating along the x direction in vacuum is 
The magnetic field 
at the moment t = 0 is:
(1) 
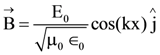
(2) 
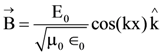
(3) 
(4) 
17. A uniform magnetic field B exists in a direction perpendicular to the plane of a square loop made of a metal wire. The wire has a diameter of 4 mm and a total length of 30 cm. The magnetic field changes with time at a steady rate dB/dt = 0.032 Ts–1. The induced current in the loop is close to (Resistivity of the metal wire is 1.23 × 10–8 Ωm)
(1) 0.53 A
(2) 0.61 A
(3) 0.34 A
(4) 0.43 A
18. Hydrogen ion and singly ionized helium atom are accelerated, from rest, through the same potential difference. The ratio of final speeds of hydrogen and helium ions is close to:
(1) 2:1
(2) 1:2
(3) 5:7
(4) 10:7
19. Two light waves having the same wavelength λ in vacuum are in phase initially. Then the first wave travels a path L1 through a medium of refractive index n1 while the second wave travels a path of length L2 through a medium of refractive index n2. After this the phase difference between the two waves is:
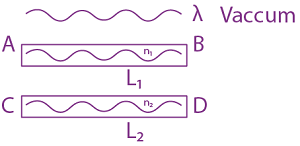
(1) 
(2) 
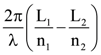
(3) 
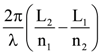
(4) 
20. A calorimeter of water equivalent 20 g contains 180 g of water at 25°C. ‘m’ grams of steam at 100°C is mixed in it till the temperature of the mixture is 31°C. The value of ‘m’ is close to (Latent heat of water = 540 cal g–1, specific heat of water = 1 cal g–1 °C–1)
(1) 2
(2) 2.6
(3) 4
(4) 3.2
21. If minimum possible work is done by a refrigerator in converting 100 grams of water at 0°C to ice, how much heat (in calories) is released to the surroundings at temperature 27°C (Latent heat of ice = 80 Cal/gram) to the nearest integer?
22. An massless equilateral triangle EFG of side ‘a’ (As shown in figure) has three particles of mass m situated at its vertices. The moment of inertia of the system about the each line EX perpendicular to EG in the plane of EFG is 
where N is an integer. The value of N is _____.
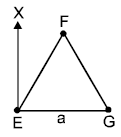
23. A galvanometer coil has 500 turns and each turn has an average area of 3 × 10–4 m2. If a torque of 1.5 Nm is required to keep this coil parallel to a magnetic field when a current of 0.5 A is flowing through it, the strength of the field (in T) is ______.
24. A block starts moving up an inclined plane of inclination 30° with an initial velocity of v0. It comes back to its initial position with velocity v0/2. . The value of the coefficient of kinetic friction between the block and the inclined plane is close to 1/1000. The nearest integer to I is____.
25. When an object is kept at a distance of 30 cm from a concave mirror, the image is formed at a distance of 10 cm from the mirror. If the object is moved with a speed of 9 cms–1, the speed (in cms–1) with which image moves at that instant is ____.
Chemistry
1. The five successive ionization enthalpies of an element are 800, 2427, 3658, 25024 and 32824 kJ mol–1. The number of valence electrons in the element is:
(1) 2
(2) 4
(3) 3
(4) 5
2. The incorrect statement is:
(1) Manganate and permanganate ions are tetrahedral
(2) In manganate and permanganate ions, the -bonding takes place by the overlap of p orbitals of oxygen and d-orbitals of manganese
(3) Manganate and permanganate ions are paramagnetic
(4) Manganate ion is green in colour and permanganate ion is purple in colour
3. Match the following drugs with their therapeutic actions:
(i) Ranitidine (a) Antidepressant
(ii) Nardil (Phenelzine) (b) Antibiotic
(iii)Chloramphenicol (c) Antihistamine
(iv) Dimetane (Brompheniramine) (d) Antacid
(e) Analgesic
(1) (i)-(d); (ii)-(a); (iii)-(b); (iv)-(c)
(2) (i)-(d); (ii)-(c); (iii)-(a); (iv)-(e)
(3) (i)-(a); (ii)-(c); (iii)-(b); (iv)-(e)
(4) (i)-(e); (ii)-(a); (iii)-(c); (iv)-(d)
4. An ionic micelle is formed on the addition of
(1) liquid diethyl ether to aqueous NaCl solution
(2) sodium stearate to pure toluene
(3) excess water to liquid 
(4) excess water to liquid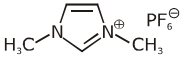 
5. Among the statements (I–IV), the correct ones are:
(I) Be has a smaller atomic radius compared to Mg.
(II) Be has higher ionization enthalpy than Al.
(III) Charge/radius ratio of Be is greater than that of Al.
(IV) Both Be and Al form mainly covalent compounds.
(1) (I), (II) and (IV)
(2) (I), (II) and (III)
(3) (II), (III) and (IV)
(4) (I), (III) and (IV)
6. Complex A has a composition of H12O6Cl3 If the complex on treatment with conc. H2SO4 loses 13.5% of its original mass, the correct molecular formula of A is: [Given: the atomic mass of Cr = 52 amu and Cl = 35 amu]
(1) [Cr(H2O)5Cl]Cl2 .H2O
(2) [Cr(H2O)4Cl2]Cl.2H2O
(3) [Cr(H2O)3Cl3].3H2O
(4) [Cr(H2O)6]Cl3
7. The decreasing order of reactivity of the following compounds towards nucleophilic substitution (SN2) is:
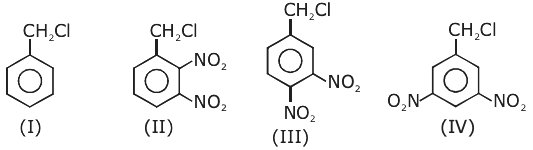
(1) (III) > (II) > (IV) > (I)
(2) (IV) > (II) > (III) > (I)
(3) (II) > (III) > (IV) > (I)
(4) (II) > (III) > (I) > (IV)
8. The increasing order of the reactivity of the following compounds in nucleophilic addition reaction is: Propanal, Benzaldehyde, Propanone, Butanone
(1) Benzaldehyde < Propanal < Propanone < Butanone
(2) Propanal < Propanone < Butanone < Benzaldehyde
(3) Butanone < Propanone < Benzaldehyde < Propanal
(4) Benzaldehyde < Butanone < Propanone < Propanal
9. The major product in the following reaction is:
10. The incorrect statement(s) among (a) – (d) regarding acid rain is (are):
(a) It can corrode water pipes.
(b) It can damage structures made up of stone.
(c) It cannot cause respiratory ailments in animals
(d) It is not harmful for trees
(1) (a), (b) and (d)
(2) (a), (c) and (d)
(3) (c) and (d)
(4) (c) only
11. 100 mL of 0.1 M HCl is taken in a beaker and to it, 100 mL of 0.1 M NaOH is added in steps of 2 mL and the pH is continuously measured. Which of the following graphs correctly depicts the change in pH?
12. Consider the hypothetical situation where the azimuthal quantum number, l, takes values 0, 1, 2, …… n + 1, where n is the principal quantum number. Then, the element with atomic number:
(1) 13 has a half-filled valence subshell
(2) 9 is the first alkali metal
(3) 8 is the first noble gas
(4) 6 has a 2p-valence subshell
13. The d-electron configuration of [Ru(en)3]Cl2 and [Fe(H2O)6]Cl2, respectively are:
(1) t42g e2g and t62g eog
(2) t62g eog and t62g eog
(3) t42g e2g and t42g e2g
(4) t62g e0g and t42g e2g
14. Consider the following molecules and statements related to them:
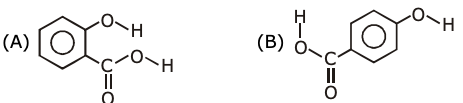
(a) (B) is more likely to be crystalline than (A)
(b) (B) has a higher boiling point than (A)
(c) (B) dissolves more readily than (A) in water
Identify the correct option from below:
(1) (a) and (c) is true
(2) only (a) is true
(3) (b) and (c) are true
(4) (a) and (b) are true
15. The strengths of 5.6 volume hydrogen peroxide (of density 1 g/mL) in terms of mass percentage and molarity (M), respectively, are: (Take the molar mass of hydrogen peroxide as 34 g/mol)
(1) 0.85 and 0.5
(2) 0.85 and 0.25
(3) 1.7 and 0.25
(4) 1.7 and 0.5
16. The compound A in the following reactions is:
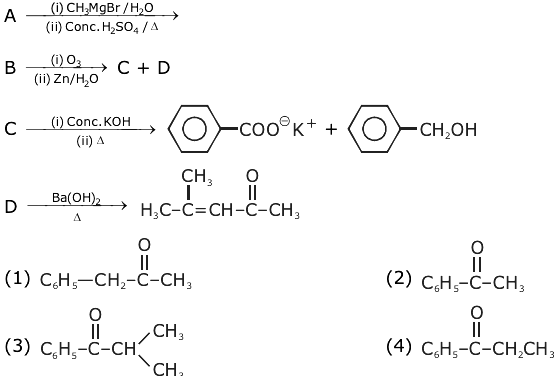
17. A mixture of one mole each of H2, He and O2 each are enclosed in a cylinder of volume V at temperature T. If the partial pressure of H2 is 2 atm, the total pressure of the gases in the cylinder is:
(1) 6 atm
(2) 14 atm
(3) 38 atm
(4) 22 atm
18. Three isomers A, B and C (mol. formula C8H11N) give the following results:
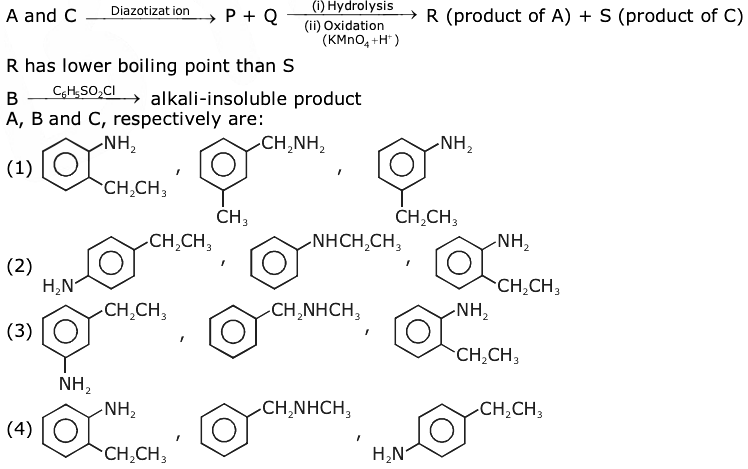
19. For the reaction 2A + 3B + (3 / 2) C → 3P, which statement is correct?
(1) 
(2) 
(3) 
(4) 
20. Consider the following reaction:
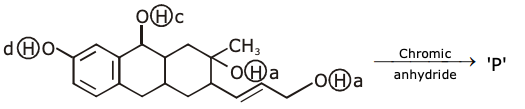
The product ‘P’ gives positive ceric ammonium nitrate test. This is because of the presence of which of these –OH group(s)?
(1) (b) only
(2) (b) and (d)
(3) (c) and (d)
(4) (d) only
21. The volume (in mL) of 0.1 N NaOH required to neutralise 10 mL of 0.1 N phosphinic acid is ___________.
22. An acidic solution of dichromate is electrolyzed for 8 minutes using 2A current. As per the following equation
The amount of Cr3+ obtained was 0.104 g. The efficiency of the process (in %) is (Take: F = 96000 C, At. mass of chromium = 52) _______.
23. If 250 cm3 of an aqueous solution containing 0.73 g of a protein A is isotonic with one litre of another aqueous solution containing 1.65 g of a protein B, at 298 K, the ratio of the molecular masses of A and B is ______ × 10–2 (to the nearest integer).
24. 6.023 × 1022 molecules are present in 10 g of a substance ‘x’. The molarity of a solution containing 5 g of substance ‘x’ in 2 L solution is _____ × 10–3.
25. The number of
groups present in a tripeptide Asp–Glu–Lys is ____.
Mathematics
1. If x3dy+xy dx = x2dy+2y dx; y(2) = e and x>1, then y(4) is equal to:
(1) 
(2) 
(3) 
(4) 
2. Let A be a 3×3 matrix such that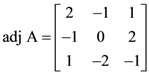 
and B = adj(adj A). If |A| = λ and |(B−1)T|=μ, then the ordered pair, (|λ|, μ) is equal to:
(1) (9, 1/81)
(2) (9, 1/9)
(3) (3, 1/81)
(4) (3, 81)
3. Let a, b, c ε R be such that a2 + b2 + c2 = 1, if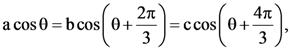 
where θ = π/9, then the angle between the vectors 
and 
is
(1) π/2
(2) 2π/3
(3) π/9
(4) 0
4. Suppose f(x) is a polynomial of degree four, having critical points at (−1, 0, 1). If T = {x ε R f(x) = f(0)}, then the sum of squares of all the elements of T is:
(1) 6
(2) 2
(3) 8
(4) 4
5. If the value of the integral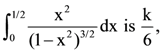 
then k is equal to:
(1) 2√3 + π
(2) 3√2 + π
(3) 3√2 − π
(4) 2√3 − π
6. If the term independent of x in the expansion of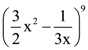 
is k, then 18 k is equal to:
(1) 5
(2) 9
(3) 7
(4) 11
7. If a triangle ABC has vertices A(−1, 7), B(−7, 1) and C(5, −5), then its orthocentre has coordinates;
(1) (−3, 3)
(2) (−3/5, 3/5)
(3) (3/5, −3/5)
(4) (3, −3)
8. Let e1 and e2 be the eccentricities of the ellipse, 
(b < 5) and the hyperbola, 
respectively satisfying e1e2 = 1. If α and β are the distances between the foci of the ellipse and the foci of the hyperbola respectively, then the ordered pair (α, β) is equal to:
(1) (8, 12)
(2) (24/5, 10)
(3) (20/3, 12)
(4) (8, 10)
9. If z1, z2 are complex numbers such that Re(z1) = |z1 − 1|, Re(z2) = |z2 − 1| and arg (z1 − z2) = π/6, then Im(z1 + z2) is equal to:
(1) 2√3
(2) 2/√3
(3) 1/√3
(4) √3/2
10. The set of all real values of λ for which the quadratic equations, (λ2 + 1) x2 − 4λx + 2 = 0 always have exactly one root in the interval (0,1) is:
(1) (−3, −1)
(2) (2, 4)
(3) (1, 3)
(4) (0, 2)
11. Let the latus rectum of the parabola y2 = 4x be the common chord to the circles C1 and C2 each of them having radius 2√5. Then, the distance between the centres of the circles C1 and C2 is:
(1) 8
(2) 8√5
(3) 4√5
(4) 12
12. The plane which bisects the line joining the points (4, −2, 3) and (2, 4, −1) at right angles also passes through the point:
(1) (0, −1, 1)
(2) (4, 0, 1)
(3) (4, 0, −1)
(4) (0, 1, −1)
13. 
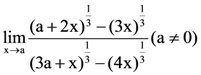is equal to:
(1) (2/9)4/3
(2) (2/3)4/3
(3) (2/3) (2/9)1/3
(4) (2/9) (2/3)1/3
14. Let xi (1 ≤ i ≤ 10)be ten observations of a random variable X. If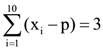 
and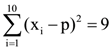 
where 0 ≠ p ε R , then the standard deviation of these observations is :
(1) 7/10
(2) 9/10
(3) 
(4) 4/5
15. The probability that a randomly chosen 5 digit number is made from exactly two digits
(1) 134/104
(2) 121/104
(3) 135/104
(4) 150/104
16. If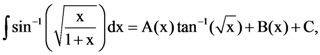
where C is a constant of integration, then the ordered pair (A(x), B(x)) can be:
(1) (x + 1, −√x)
(2) (x – 1, −√x)
(3) (x + 1, √x)
(4) (x – 1, √x)
17. If the sum of the series 
nth term is 488 and then nth term is negative, then:
(1) n = 60
(2) n = 41
(3) nth term is −4
(4) nth term is 
18. Let p, q, r be three statements such that the truth value of (p ˄ q) → (∼q ˅ r) is F. Then the truth values of p, q, r are respectively:
(1) F, T, F
(2) T, F, T
(3) T, T, F
(4) T, T, T
19. If the surface area of a cube is increasing at a rate of 3.6 cm2/sec, retaining its shape; then the rate of change of its volume (in cm3/sec), when the length of a side of the cube is 10cm, is :
(1) 9
(2) 10
(3) 18
(4) 20
20. Let R1 and R2 be two relations defined as follows:
R1 = {(a,b) ∈ R2 : a2 + b2 ∈ Q} and
R2 = {(a,b) ∈ R2 : a2 + b2 ∉Q}, where Q is the set of all rational numbers. Then :
(1) R1 is transitive but R2 is not transitive
(2) R1 and R2 are both transitive
(3) R2 is transitive but R1 is not transitive
(4) Neither R1 nor R2 is transitive
21. If m arithmetic means (A.Ms) and three geometric means (G.Ms) are inserted between 3 and 243 such that 4th A.M. is equal to 2nd G.M., then m is equal to
22. Let a plane P contain two lines 
and 
If Q(α, β, γ) is the foot of the perpendicular drawn from the point M(1, 0, 1) to P, then 3(α + β + γ) equals_____
23. Let S be the set of all integer solutions, (x, y, z), of the system of equations
x – 2y + 5z = 0
−2x + 4y + z = 0
−7x + 14y + 9z = 0
such that 15 ≤ x2 + y2 + z2 ≤ 150. Then, the number of elements in the set S is equal to ______
24. The total number of 3 digit numbers, whose sum of digits is 10, is:
25. If the tangent to the curve, y = ex at a point (c, ec) and the normal to the parabola, y2 = 4x at the point (1,2) intersect at the same point on the x-axis, then the value of c is:
Latest Govt Job & Exam Updates: