Solved Paper-2014
VIT
Engineering Entrance Exam
Mathematics
1. If the vertices of a triangle are A(0, 4, 1), B(2, 3, −1) and C(4, 5, 0), then the orthocenter of ∆ABC, is
(a) (4, 5, 0)
(b) (2, 3, −1)
(c) (−2, 3, −1)
(d) (2, 0, 2)
2. The equation of normal to the curve y (1 + x)y + sin−1 (sin2x) at x = 0 is
(a) x + y = 1
(b) x – y = 1
(c) x + y = −1
(d) x – y = −1
3. The value of c from the Lagrange’s mean value theorem for which 
in [1, 5] is
(a) 5
(b) 1
(c) √15
(d) None of these
4. If 
then A ∙ (adj A) is equal to
(a) A
(b) |A|
(c) A| ∙ I
(d) None of these
5. If there is an error of k% in measuring the edge of a cube, then the per cent error in estimating its volume is
(a) k
(b) 3k
(c) k/3
(d) None of these
6. If the system of equations x + ky – z = 0, 3x – ky – z = 0 and x – 3y + z = 0, has non-zero solution, then k is equal to
(a) −1
(b) 0
(c) 1
(d) 2
7. If the points (1, 2, 3) and (2, −1, 0) lie on the opposite sides of the plane 2x + 3y – 2z = k, then
(a) k < 1
(b) k > 2
(c) k < 1 or k > 2
(d) 1 < k < 2
8. If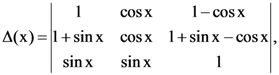 
then is equal to
(a) 1/4
(b) 1/2
(c) 0
(d) −1/4
9. Let f ′(x), be differentiable ∀ If f(1) = −2 and f′(x) ≥ 2 ∀ x ∈ [1, 6], then
(a) f(6) < 8
(b) f(6) ≥ 8
(c) f(6) ≥ 5
(d) f(6) ≤ 5
10. If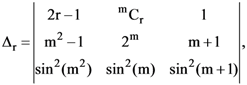 
then the value of 
is
(a) 1
(b) 0
(c) 2
(d) None of these
11. Two lines 
and 
intersect at a point, if k is equal to
(a) 2/9
(b) 1/2
(c) 9/2
(d) 1/6
12. The minimum value of 
is
(a) e
(b) 1/e
(c) e2
(d) e3
13. The triangle formed by the tangent to the curve f(x) = x2 + bx – b at the point (1, 1) and the coordinate axes lies in the first quadrant. If its area is 2, then the value of b is
(a) −1
(b) 3
(c) −3
(d) 1
14. The statement (p ⇒ q) ⇔ (~p ⋀ q) is a
(a) tautology
(b) contradiction
(c) Neither (a) nor (b)
(d) None of these
15. If 
then x2 + y2 is equal to
(a) 3x – 4
(b) 4x – 3
(c) 4x + 3
(d) None of these
16. The negation of (~p ⋀ q) ⋁ (p ⋀~ q) is
(a) (p ⋁ ~q) ⋁ (~p⋁q)
(b) (p ⋁ ~q) ⋀ (~p ⋁ q)
(c) (p ⋀ ~q) ⋀ (~p ⋁ q)
(d) (p ⋀ ~q) ⋀ (p ⋁ ~q)
17. The normals at three points P, Q and R of the parabola = y2 = 4ax meet at (h, k). The centroid of the ∆PQR lies on
(a) x = 0
(b) y = 0
(c) x = −a
(d) y = a
18. The minimum area of the triangle formed by any tangent to the ellipse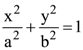 
with the coordinate axes is
(a) 
(b) 
(c) 
(d) 
19. If the line lx + my – n = 0 will be a normal to the hyperbola, then 
where k is equal to
(a) n
(b) n2
(c) n3
(d) None of these
20. If cos α + i sin α, b = cos β + i sin β, c = cos γ + i sin γ and 
then cos(β – γ) + cos(γ – α) + cos(α – β) is equal to
(a) 3/2
(b) −3/2
(c) 0
(d) 1
21. If |z + 4| ≤ 3, then the greatest and the least value of |z + 1| are
(a) −1, 6
(b) 6, 0
(c) 6, 3
(d) None of these
22. The angle between lines joining the origin to the point of intersection of the line √3x + y = 2 and the curve y2 – x2 = 4 is
(a) 
(b) π/6
(c) 
(d) π/2
23. If the area of the triangle on the complex plane formed by the points z, z + iz and iz is 200, then the value of 3|z| must be equal to
(a) 20
(b) 40
(c) 60
(d) 80
24. Equation of the chord of the hyperbola 25x2 – 16y2 = 400 which is bisected at the point (6, 2), is
(a) 6x – 7y = 418
(b) 75x – 16y = 418
(c) 25x – 4y = 400
(d) None of these
25. If a plane meets the coordinates axes at A, B and C such that the centroid of the triangle is (1, 2, 4), then the equation of the plane is
(a) x + 2y + 4z = 12
(b) 4x + 2y + z = 12
(c) x + 2y + 4z = 3
(d) 4x + 2y + z = 3
26. The volume of the tetrahedron include between the plane 3x + 4y – 5z – 60 = 0 and the coordinate planes is
(a) 60
(b) 600
(c) 720
(d) 400
27. 
is equal to
(a) 0
(b) 4
(c) 8
(d) 1
28. The value of 
where [∙] is the greatest integer function, is
(a) 2 – √2
(b) 2 + √2
(c) √2 – 1
(d) √2 – 2
29. If 
then the expression for l(m, n) in terms of l(m + 1, n+1) is
(a) 
(b) 
(c) 
(d) 
30. The area in the first quadrant between x2 + y2 = π2 and y = sin x is
(a) 
(b) 
(c) 
(d) 
31. The area bounded y = xe|x| and lines |x| = 1, y = 0 is
(a) 4 sq units
(b) 6 sq units
(c) 1 sq unit
(d) 2 sq units
32. The solution of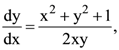 
satisfying y(1) = 0 is given by
(a) hyperbola
(b) circle
(c) ellipse
(d) parabola
33. If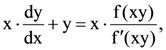 
then f(xy) is equal to
(a) 
(b) 
(c) 
(d) 
34. The differential equation of the rectangular hyperbola, where axes are the asymptotes of the hyperbola, is
(a) 
(b) 
(c) 
(d) 
35. The length of longer diagonal of the parallelogram constructed on 5a + 2b and a – 3b, if it is given that |a| = 2√2, |b| = 3 and the angle between a and b is π/4, is
(a) 15
(b) √113
(c) √593
(d) √369
36. If r = αb × c + βc × a + γa × b and [a b c] = 1, then α + β + γ is equal to
(a) r ∙ [b × c + c × a + a × b]
(b) 
(c) 2r ∙ (a + b + c)
(d) 4
37. If a, b, c are three non-coplanar vectors and p , q, r are reciprocal vectors, then (la + mb + nc) ∙ (lp + mq + nr) is equal to
(a) l + m +n
(b)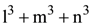 
(c) 
(d) None of these
38. If the integers m and n are chosen at random from 1 to 100, then the probability that a number of the form 7n + 7m is divisible by 5, equals to
(a) 1/4
(b) 1/2
(c) 1/8
(d) 1/3
39. Let X denote the sum of the numbers obtained when two fair dice are rolled. The variance and standard deviation of X are
(a) 
(b) 
(c) 
(d) 
40. A four-digit number is formed by the digits 1, 2, 3, 4 with no repetition. The probability that the number is odd, is
(a) zero
(b) 1/3
(c) 1/4
(d) None of these
Latest Govt Job & Exam Updates: