VITEE-2016 Solved Paper
PART III MATHEMATICS
1. The solution of the differential equation ![]()
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
2. A tetrahedron has vertices at O(0, 0, 0), A(1, 2, 1) B(2, 1, 3) and C(−1, 1, 2). Then the angle between the faces OAB and ABC will be
(a) 120°
(b) cos−1(17/31)
(c) 30°
(d) 90°
3. The foci of the ellipse ![]() and the hyperbola
and the hyperbola ![]() coincide then value of b2 is
coincide then value of b2 is
(a) 1
(b) 5
(c) 7
(d) 9
4. If the tangent to the function y = f(x) at (3, 4) makes an angle of 3π/4 with the positive direction of x-axis in anticlockwise direction then f ʹ(3) is
(a) −1
(b) 1
(c) 1/√3
(d) √3
5. The probability of India winning a test match against Australia is 1/2 assuming independence from match to match. The probability that in a match series India’s second win occurs at third test match is
(a) 1/8
(b) 1/4
(c) 1/2
(d) 2/3
6. If ![]() then the value of
then the value of ![]() is (given that
is (given that ![]()
(a) −7
(b) 7
(c) 14
(d) −14
7. If f(x) = x2, g(x) = 2x, 0 ≤ x ≤ 2 then the value of 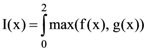 is
is
(a) 10/3
(b) 1/3
(c) 11/3
(d) 32
8. If A and B are matrices and B = ABA−1 then the value of (A + B) (A – B) is
(a) A2 + B2
(b) A2 – B2
(c) A + B
(d) A – B
9. The value of (1 + ω –ω2)7 is
(a) 128ω2
(b) −128ω2
(c) 128ω
(d) −128ω
10. The moment about the point ![]() acting through the point 2i + 3j + k is
acting through the point 2i + 3j + k is
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
11. If g(x) is a polynomial satisfying g(x) g(y) = g(x) + g(y) + g(xy) – 2 for all real x and y and g(2) = 6 then ![]() is
is
(a) 9
(b) 10
(c) 25
(d) 20
12. The equation of one of the common tangents to the parabola y2 = 8x and x2 + y2 – 12x + 4 = 0 is
(a) y = x + 2
(b) y = x – 2
(c) y = x + 2
(d) None of these
13. If ![]() then the value of y is
then the value of y is
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
14. What is the area of a loop of the curve r = a sin 3θ?
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
15. Convert the hexadecimal numeral ABCD into binary numeral
(a) (1010101111001101)2
(b) (1001000011111111)2
(c) (1111110000010001)2
(d) (1000100100111100)2
16. The normal at the point (at12, 2at1) on the parabola, cuts the parabola again at the point whose parameter is
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
17. The distance moved by the particle in time t is given by s = t3 – 12t2 + 6t + 8. At the instant, when its acceleration is zero the velocity is :
(a) 42
(b) −42
(c) 48
(d) −48
18. The logical expression X, in its simplest form for the truth table

(a) X = a, b
(b) X = a + b
(c) X = a’.b
(d) X = a.b’
19. The value of is equal ![]() to
to
(a) −3/4
(b) 3/4
(c) 1/16
(d) 1/4
20. Consider the objective function Z = 40x + 50y. The minimum number of constraints that are required to maximize Z are
(a) 4
(b) 2
(c) 3
(d) 1
21. In a culture the bacteria count is 1,00,000. The number is increased by 10% in 2 hours. In how many hours will the count reach 2,00,000 if the rate of growth of bacteria is proportional to the number present.
(a) ![]()
(b) 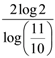
(c) ![]()
(d) 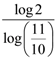
22. The value of ![]() is
is
(a) π/6
(b) π/4
(c) π/3
(d) π/2
23. If a = cos 2α + i sin 2α, b = cos 2β + i sin 2β, c = cos 2γ + i sin 2γ and d = cos 2δ + i sin 2δ, then ![]()
(a) √2 cos(α + β + γ + δ)
(b) 2 cos (α + β + γ + δ)
(c) cos((α + β + γ + δ)
(d) None of these
24. If the mean of a binomial distribution is 25, then its standard deviation lies in the interval
(a) [0, 5)
(b) (0, 5]
(c) [0, 25)
(d) (0, 25]
25. Number of ways of selecting three squares on a chessboard so that all the three be on a diagonal line of the board or parallel to it is
(a) 196
(b) 126
(c) 252
(d) 392
26. If A and B are two matrices such than rank of A = m and rank of B = n, then
(a) rank (AB) = mn
(b) ran (AB) ≥ ran (A)
(c) ran (AB) ≥ rank (B)
(d) rank (AB) ≤ min (rank A, rank B)
27. A variable plane remains at constant distance p from the origin. If it meets coordinate axes at points A, B, C then the locus of the centroid of ∆ ABC is
(a) x−2 + y−2 + z−2 = 9p−2
(b) x−3 + y−3 + z−3 = 9p−3
(c) x2 + y2 + z2 = 9p2
(d) x3 + y3 + z3 = 9p3
28. While shuffling a pack of 52 playing cards, 2 are accidentally dropped. The probability that the missing cards to be of different colours is
(a) 29/52
(b) 1/2
(c) 26/51
(d) 27/51
29. Which of the following is INCORRECT for the hyperbola x2 – 2y2 – 2x + 8y – 1 = 0
(a) It eccentricity is √2
(b) Length of the transverse axis is 2√3
(c) Length of the conjugate axis is 2√6
(d) Latus rectum is 4√3
30. A box contains 20 identical balls of which 10 are blue and 10 are green. The balls are drawn at random from the box one at a time with replacement. The probability that a blue ball is drawn 4th time on the 7th draw is
(a) 27/32
(b) 5/64
(c) 5/32
(d) 1/2
31. The number of common tangents to the circles x2 + y2 – 6x – 14y + 48 = 0 and x2 + y2 – 6x = 0 is
(a) 1
(b) 2
(c) 0
(d) 4
32. The solution of the equation cos2θ + sin θ + 1 = 0, lies in the interval
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
33. If f(x) = (1 + x)2/x for x ≠ 0 and f(0) = e2 is
(a) left continuous only at x = 0
(b) right continuous only at x = 0
(c) continuous at x = 0
(d) discontinuous at x = 0
34. If y = yx/lnx then ![]() at x = e is
at x = e is
(a) e
(b) 2e log 2
(c) log 2
(d) 0
35.![]() is equal to
is equal to
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
36. If the letters of the word KRISNA are arranged in all possible ways and these words are written out as a in a dictionary, then the rank of the word KRISNA is
(a) 324
(b) 341
(c) 359
(d) None of these
37. The shortest distance between the lines x = y + 2 = 6z – 6 and x + 1 = 2y = −12z is
(a) 1/2
(b) 2
(c) 1
(d) 3/2
38. The domain and range of the function f given by f(x) = 2 – |x – 5| is
(a) Domain = R+, Range = (−∞, 1]
(b) Domain = R, Range = (−∞, 2)
(c) Domain = R, Range = (−∞, 2)
(d) Domain = R+, Range = (−∞, 2]
39. The number of surjective function from A to B where A = A{1, 2, 3, 4} and B = {a, b} is
(a) 14
(b) 12
(c) 2
(d) 15
40. If f(a + b – x) = f(x), then 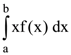 is equal to
is equal to
(a) 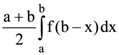
(b) 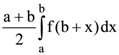
(c) 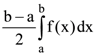
(d) 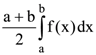
Latest Govt Job & Exam Updates: