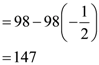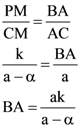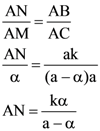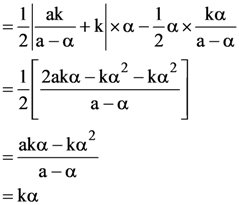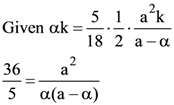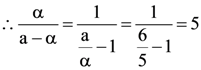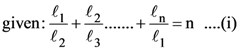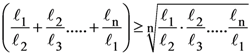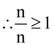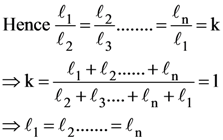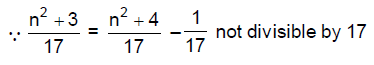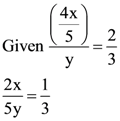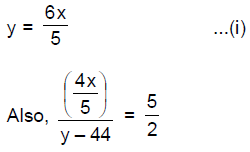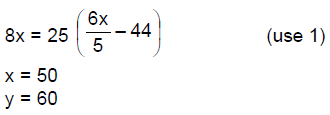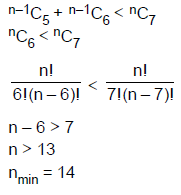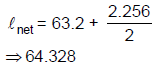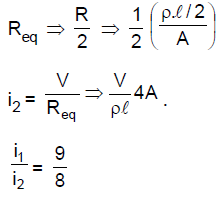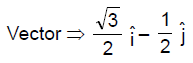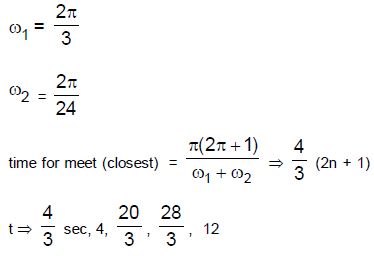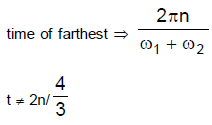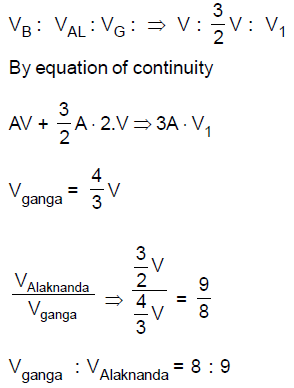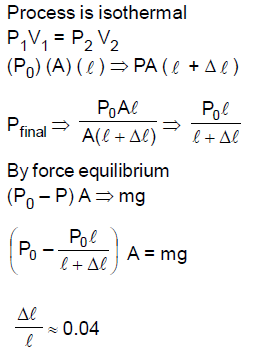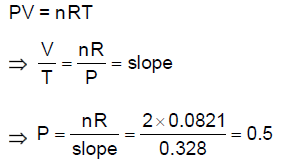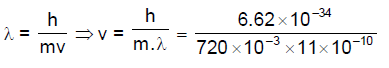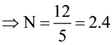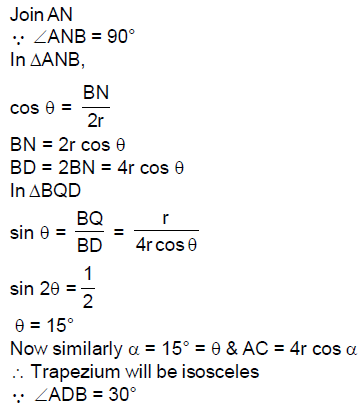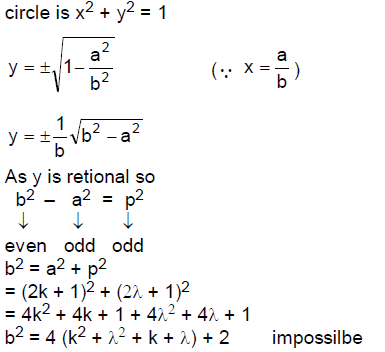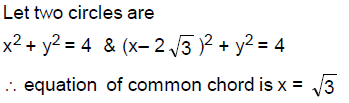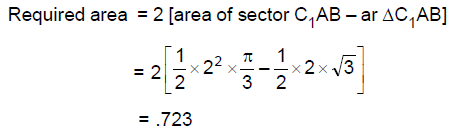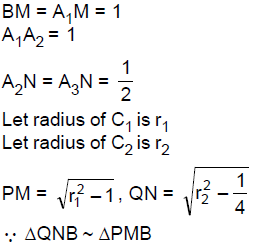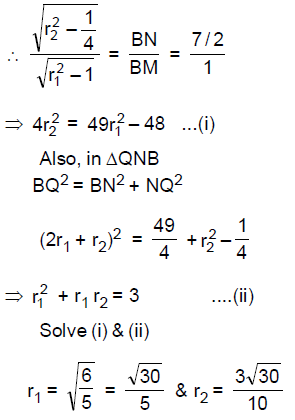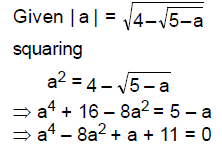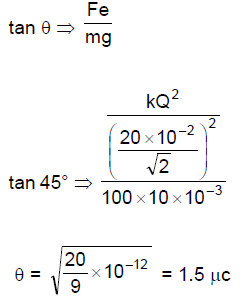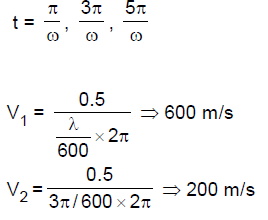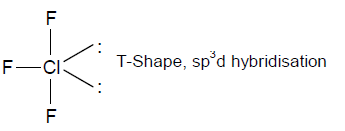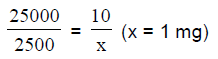KVPY Question Paper 2017 Stream SA Held on 19-11-2017

Section 1-Part A-Mathematics

 

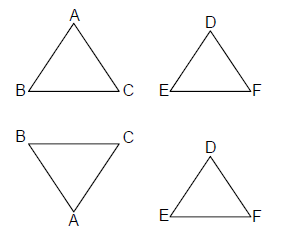
1. Suppose BC is a given line segment in the plane and T is a scalene triangle. The number of points A in the plane such that the triangle with vertices A,B,C (in some order) is similar to triangle T is

(A)  4

(B)  6

(C)  12

(D)  24

Show Answer

2. The number of positive integers n in the set {2, 3, …….., 200) such that 1/n has a terminating decimal expansion is

(A)  16

(B)  18

(C)  40

(D)  100

Show Answer

3. If a,b,c are real numbers such that a + b + c = 0 and a² + b² + c² = 1, then (3a + 5b – 8c)² + (–8a + 3b + 5c)² + (5a – 8b + 3c)² is equal to

(A)  49

(B)  98

(C)  147

(D)  294

Show Answer

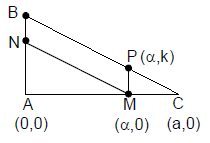
4. Let ABC be a triangle and M be a point on side AC closer to vertex C than A. Let N be a point on side AB such that MN is parallel to BC and let P be a point on side BC such that MP is parallel to AB. If the area of the quadrilateral BNMP is equal to 5/18th of the area of triangle ABC, then the ration AM/MC equals.

(A)  5

(B)  6

(C)  18/5

(D)  15/2

Show Answer

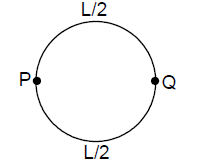
5. Let n ≥ 4 be a positive integer and let ℓ₁, ℓ₂, ………, ℓ_n be the lengths of the sides of arbitrary n-sided non-degenerate polygon P. Suppose

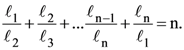
Consider the following statements :

I. The lengths of the sides of P are equal.

II. The angles of P are equal.

III. P is a regular polygon if it is cyclic.

Then

(A)  I is true and I implies II

(B)  II is true

(C)  III is false

(D)  I and III are true

Show Answer

6. Consider the following statements. For any integer n,

I. n² + 3 is never divisible by 17.

II. n² + 4 is never divisible by 17.

Then

(A)  both I and II are true

(B)  both I and II are false

(C)  I is false and II is true

(D)  I is true and II is false

Show Answer

7. Let S be the set of all ordered pairs (x,y) of positive integers, with HCF (x,y) = 16 and LCM (x,y) = 48000. The number of elements in S is

(A)  4

(B)  8

(C)  16

(D)  32

Show Answer

8. Consider the set A of natural numbers n whose units digit is nonzero, such that if this units digit is erased, then the resulting number divides n. If K is the number of elements in the set A, then

(A)  K is infinite

(B)  K is finite but K > 100

(C)  25≤ K ≤ 100

(D)  K < 25

Show Answer

Such numbers are = 9 from 11 to 19

4 i.e. (22, 24, 26, 28)

3 i.e. (33, 36, 39)

2 i.e. (44, 48)

5 i.e. (55, 66, 77, 88, 99)

9. There are exactly twelve Sundays in the period from January 1 to march 31 in a certain year. Then the day corresponding to February 15 in that year is

(A)  Tuesday

(B)  Wednesday

(C)  Thursday

(D)  not possible to determine from the given data

Show Answer

10. Consider a three-digit number with the following properties:

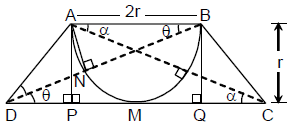
I. If its digits in units place and tens place are interchanged, the number increases by 36;

II. If its digits in units place and hundreds place are interchanged, the number decreases by 198.

Now suppose that the digits in tens place and hundreds place are interchanged. Then the number.

(A)  increases by 180

(B)  decreases by 270

(C)  increases by 360

(D)  decreases by 540

Show Answer

Let Three digit No is 100 a + 10 b + c

Given 100 a + 10 b + c = 100 a + 10 c + b – 36

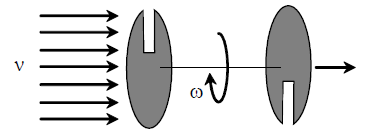
9b – 9c + 36 = 0

c = b + 4

b = c – 4 …(i)

Also given 100 a + 10 b + c = 100c + 10 b + a + 198

99 a – 99 c = 198

a = c + 2 …(ii)

∴ Now 100 a + 10 b + c – (100 b + 10 a + c)

= 90 (a – b)

= 90 ( c + 2 – c + 4) (use (i) & (ii))

= 540

∴ value decrease by 540

11. Consider four triangles having sides (5,12,9), (5,12,11), (5,12,13) and (5,12,15). Among these, the triangle having maximum area has sides

(A)  (5,12,9)

(B)  (5, 12, 11)

(C)  (5,12,13)

(D)  (5,12,15)

Show Answer

12. In a classroom, one-fifth of the boys leave the class and the ratio of the remaining boys to girls is 2:3. If further 44 girls leave the class, the ratio of boys to girls is 5 : 2. How many more boys should leave the class so that the number of boys equals that of girls?

(A)  16

(B)  24

(C)  30

(D)  36

Show Answer

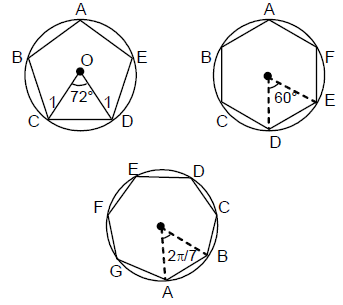
13. Let X,Y,Z be respectively the areas of a regular pentagon, regular hexagon and regular heptagon which are inscribed in a circle of radius 1. Then

(A) 

(B)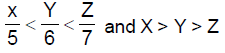 

(C)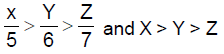 

(D) 

Show Answer

14. The least value of a natural number n such that , is

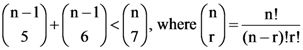
(A)  12

(B)  13

(C)  14

(D)  15

Show Answer

15. In a Mathematics test, the average marks of boys is x% and the average marks of girls is y% with x≠ If the average marks of all students is z%, the ration of the number of girls to the total number of students is

(A) 

(B) 

(C) 

(D) 

Show Answer

Section 2-Part A-Physics

16. Particle sused in the Rutherford’s scattering experiment to deduce the structure of atoms

(A)  had atomic number 2 and were fully ionised.

(B)  had atomic number 2 and were neutral.

(C)  had atomic number 4 and were fully ionised.

(D)  had atomic number 4 and were neutral.

Show Answer

α-particle bombard during experiment

α-particles ionized helium

17. The number of completely filled shells for the element ₁₆S³² is

(A)  1

(B)  2

(C)  3

(D)  4

Show Answer

18. In an experiment on simple pendulum to determine the acceleration due to gravity, a student measures the length of the thread as 632 cm and diameter of the pendulum bob as 2.256 cm. The student should take the length of the pendulum to be

(A)  64.328 cm

(B)  64.36 cm

(C)  65.456 cm

(D)  65.5 cm

Show Answer

19. A uniform metallic wire of length L is mounted in two configurations. In configuration I (triangle), it is an equilateral triangle and a voltage V is applied to corners A and B. In configuration 2 (circle), it is bent in the form of a circle, and the potential v is applied at diametrically opposite points P and Q. The ratio of the power dissipated in configuration 1 to configuration 2 is.

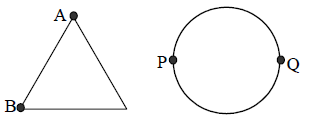
(A)  2/3

(B)  9/8

(C)  5/4

(D)  7/8

Show Answer

20. Six objects are placed at the vertices of a regular hexagon. The geometric center of the hexagon is at the origin with objects 1 and 4 on the x-axis (see figure). The mass of the kth object is mk = k M |cosq_k| where i is an integer, M is a constant with dimension of mass, and q_k is the angular position of the kth verted measured from the positive x-axis in the counter-clockwise sense. If the net gravitational force on a body at the centroid vanishes, the value of i is

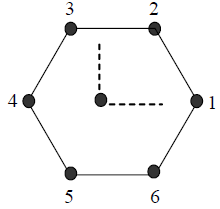
(A)  0

(B)  1

(C)  2

(D)  3

Show Answer

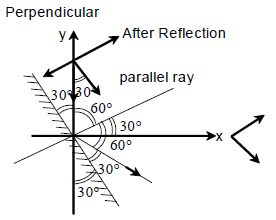
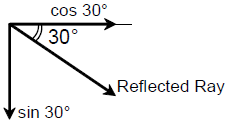
21. A mirror is placed at an angle of 30° with respect to y-axis (see figure). A light ray travelling in the negative y-direction strikes the mirror. The direction of the reflected ray is given by the vector

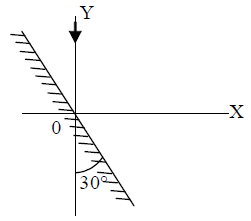
(A) 

(B) 

(C) 

(D) 

Show Answer

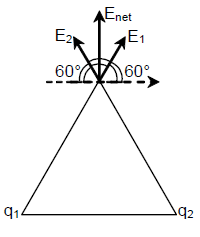
22. A total charge q is divided as q₁ and q₂ which are kept at two of the vertices of an equilateral triangle of side a. The magnitude of the electric field E at the third vertex of the triangle is to be depicted schematically as a function of x = q₁/q. Choose the correct figure.

(A)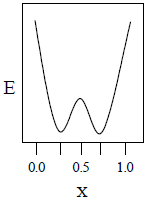 

(B)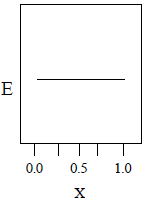 

(C)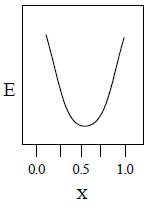 

(D)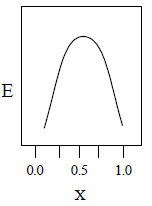 

Show Answer

23. The refractive index of water in a biology laboratory tank varies as 1.33 + 0.002/λ², where λ is the wavelength of light. Small pieces of organic matter of different colours are seen at the bottom of the tank using a travelling microscope. Then the image of the organic matter appears

(A)  deeper for the violet pieces than the green ones.

(B)  shallower for the blue pieces than the orange ones.

(C)  at the same depth for both the blue and orange pieces.

(D)  deeper for the green pieces than the red ones.

Show Answer

24. Two students P and Q perform an experiment to verify Ohm’s law for a conductor with resistance R. They use a current source and a voltmeter with least counts of 0.1 mA and 0.1 mV, respectively. The plots of the variation of voltage drop (V) across R with current (I) for both are shown below

 

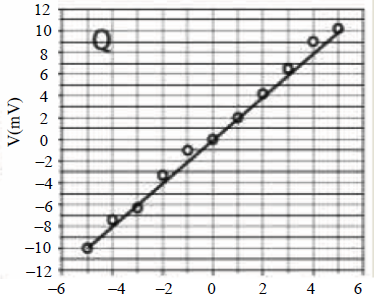
The statement which is most likely to be correct is:

(A)  P has only random error (s).

(B)  Q has only systematic error (s).

(C)  Q has both random and systematic errors.

(D)  P has both random and systematic errors.

Show Answer

25. A cylindrical vessel of base radius R and height H has a narrow neck of height h and radius r at one end (see figure). The vessel is filled with water (density ρ_w) and its neck is filled with immiscible oil (density ρ_O). Then the pressure at

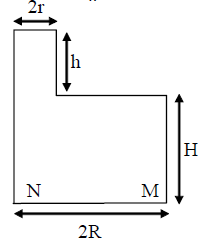
(A) 

(B)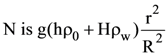 

(C) 

(D)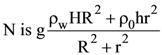

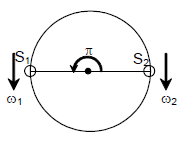
Show Answer

26. Two cars S₁ and S₂ are moving in coplanar concentric circular tracks in the opposite sense with the periods of revolution 3 min and 24 min, respectively. At time t = 0, the cars are farthest apart. Then, the two cars will be

(A)  closest to each other at t = 12 min and farthest at t = 18 min.

(B)  closest to each other at t = 3 min and farthest at t = 24 min

(C)  closest to each other at t = 6 min and farthest at t = 12 min

(D)  colsest to each other at t = 12 min and farthest at t = 24 min

Show Answer

27. In the circuit shown below, a student performing Ohm’s law experiment accidently puts the voltmeter and the ammeter as shown in the circuit below; the reading in the voltmeter will be close to

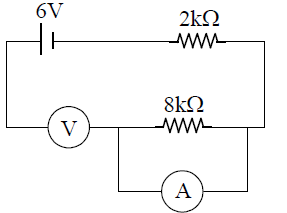
(A)  0 V

(B)  4.8 V

(C)  6.0 V

(D)  1.2 V

Show Answer

28. The Bhagirathi and the Alaknanda merge at Deoprayag to form the Ganga with their speeds in the ratio 1 :1.5. The cross-sectional areas of the Bhagirathi, the Alaknanda and the Ganga are in the ratio 1 : 2 :3. Assuming streamline flow, the ratio of the speed of Ganga to that of the Alaknands is

(A)  7 : 9

(B)  4 : 3

(C)  8 : 9

(D)  5 : 3

Show Answer

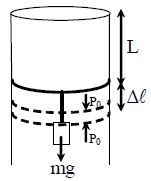
29. A long cylindrical pipe of radius 20 cm is closed at its upper end and has an airtight piston of negligible mass as shown. When a 50 Kg mass is attached to the other end of the piston, it moves down by a distance ∆l before coming to equilibrium. Assuming air to be an ideal gas, ∆l/L (see figure) is close to (g = 10 ms² , atmospheric pressure is 105 Pascal),

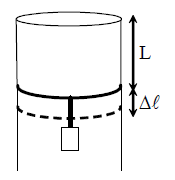
(A)  0.01

(B)  0.02

(C)  0.04

(D)  0.09

Show Answer

30. The word ‘’KVPY’’ is written on a board and viewed through different lens such that board is at a distance beyond the focal length of the lens.

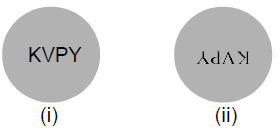
ignoring magnification effects, consider the following statements

(I) Image (i) has been viewed from the planar side of a plano-concave lens and image

(ii) from the planar side of a plano-convex lens.

(II) Image (i) has been viewed from the concave side of a plano-concave lens and image (ii) from the convex side of a plano-convex lens.

(III) Image (i) has been viewed from the concave side of a plano-concave lens and image (ii) from the planar side of a plano-convex lens.

(IV) Image (i) has been viewed from the planar side of a plano-concave lens and image (ii) from the convex side of a plano-convex lens.

Which of the above statements are correct?

(A)  Only (III)

(B)  Only (IV)

(C)  Only (III) and (IV)

(D)  All four

Show Answer

Section 3 Part 1 Chemistry

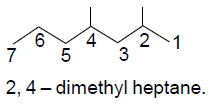
31. The IUPAC name for the following compound is

(A)  4, 6-dimethylheptane

(B)  1, 3, 5-trimethylhexane

(C)  2, 4-dimethylheptane

(D)  2, 4, 6-trimethylhexane

Show Answer

32. The stability of carbocations

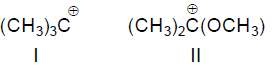
follows the order

(A)  III < IV < II < I

(B)  III < IV < I < II

(C)  IV < III < II < I

(D)  IV < III < I < II

Show Answer

33. The acidity of compounds I-IV in water

I. Ethanol

II. Acetic Acid

III. Phenol

IV. Acetonitrile

follows the order

(A)  IV < I < III < II

(B)  I < II < III < IV

(C)  IV < I < II < III

(D)  IV < III < I < II

Show Answer

34. In the following reaction

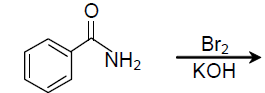
the major product is

(A)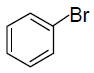 

(B)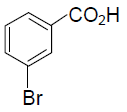 

(C)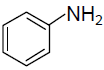 

(D)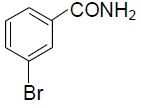 

Show Answer

35. The reddish brown precipitate formed in the Fehling’s test for aldehydes (RCHO) is due to the formation of

(A)  Cu

(B)  Cu₂O

(C)  CuO

(D)  (RCOO)₂Cu

Show Answer

36. The reducing ability of the metals K, Au, Zn and Pb follows the order

(A)  K > Pb > Au > Zn

(B)  Pb > K > Zn > Au

(C)  Zn > Au > K > Pb

(D)  K > Zn > Pb > Au

Show Answer

37. White phosphorous catches fire in air to produce dense white fumes. This is due to the formation of

(A)  P₄O₁₀

(B)  PH₃

(C)  H₃PO₃

(D)  H₃PO₂

Show Answer

38. The maximum number of electrons that can be filled in the shell with the principal quantum number n = 4 is

(A)  64

(B)  26

(C)  18

(D)  32

Show Answer

39. At a constant pressure P, the plot of volume (V) as a function of temperature (T) for 2 moles of an ideal gas gives a straight line with a slope 0.328 L K^–1. The value of P (in atm) is closest to

[Gas constant, R = 0.0821 L atm mol^–1 K^–1]

(A)  0.25

(B)  0.5

(C)  1.0

(D)  2.0

Show Answer

40. Which of the following transformations can be carried out by using HI as a reducing agent, under acidic conditions ?

[Given : I2(s) → 2I^– E^θ = 0.54 V]

(i) Cu⁺ → Cu(s) E^θ = 0.52 V

(ii) Cr³⁺ → Cr²⁺ E^θ = – 0.41 V

(iii) Fe³⁺ → Fe²⁺ E^θ = 0.77 V

(iv) Fe²⁺ → Fe(s) E^θ = – 0.44 V

(A)  (i) and (iii)

(B)  (ii) and (iv)

(C)  only (iii)

(D)  only (ii)

Show Answer

41. C⁶⁰ emerging from a source at a speed (v) has a de Broglie wavelength of 11.0 Å. The value of v (in m s^–1) is closest to

[Planck’s constant h = 6.626 × 10^–34 J s]

(A)  0.5

(B)  2.5

(C)  5.0

(D)  30

Show Answer

42. The lattice energies of NaCl, NaF, KCl and RbCl follow the order

(A)  KCl < RbCl < NaCl < NaF

(B)  NaF < NaCl < KCl < RbCl

(C)  RbCl < KCl < NaCl < NaF

(D)  NaCl < RbCl < NaF < KC

Show Answer

43. The oxidation states of P atom in POCl₃, H₂PO₃ and H₄P₂O₆, respectively, are

(A)  1.2

(B)  2.4

(C)  4.8

(D)  0.6

Show Answer

44. A solution (5 mL) of an acid X is completely neutralized by y mL of 1M NaOH. The same volume (y ML) of 1M NaOH is required to neutralize 10 mL of 0.6 M of H₂SO₄ The normality (N) of the acid X is

(A)  1.2

(B)  2.4

(C)  4.8

(D)  0.6

Show Answer

45. 1.25 g of a metal (M) reacts with oxygen completely to produce 1.68 g of metal oxide. The empirical formula of the metal oxide is

[molar mass of M and O are 69.7 g mol^–1 and 16.0 g mol^–1, respectively]

(A)  M₂O

(B)  M₂O₃

(C)  MO₂

(D)  M₃O_­4

Show Answer

Section 4 Part-A Biology

46. According to Watson-Crick model, hydrogen bonding in a double-stranded DNA occurs between

(A)  adenine and guanine

(B)  adenine and thymine

(C)  cytosine and adenine

(D)  guanine and thymine

Show Answer

47. Which ONE of the following statements about mitosis is CORRECT ?

(A) One nucleus gives rise to 4 nuclei

(B) Homologous chromosomes synapse during anaphase

(C) The centromeres separate at the onset of anaphase

(D) Non-sister chromatids recombine

Show Answer

48. Gaseous exchange of oxygen and carbon dioxide between alveolar air and capillaries takes place by

(A)  Active transport

(B)  Diffusion

(C)  Carrier-mediated transport

(D)  Imbibition

Show Answer

49. Of the periods listed below, which ONE is the earliest period when Ostracoderms, the jawless and finless fishes, appeared?

(A)  Devonian period

(B)  Cambrian period

(C)  Carboniferous period

(D)  Silurian period

Show Answer

50. Scurvy is caused by the deficiency of

(A)  Nicotinic acid

(B)  Ascorbic acid

(C)  Pantothenic acid

(D)  Retinoic acid

Show Answer

51. Optical activity of DNA is due to its

(A)  Bases

(B)  Sugars

(C)  Phosphate

(D)  Hydrogen bonds

Show Answer

52. The monarch butterfly avoids predators such as birds by

(A) Changing color frequently

(B) Flying away from the predator swiftly

(C) Producing a chemical obnoxious to the predator

(D) Producing ultrasonic waves

Show Answer

53. Filariasis is caused by

(A) Entamoeba histolytica

(B) Plasmodium falciparum

(C) Trypanosoma brucei

(D) Wuchereria bancrofti

Show Answer

54. Which ONE of the following conversions does NOT happen under anaerobic conditions ?

(A)  Glucose to ethanol by Saccharomyces.

(B)  Lactose to lactic acid by Lactobacillus.

(C)  Glucose to CO₂ and H₂O by Saccharomyces.

(D)  Cellulose to glucose by Cellulomonas.

Show Answer

55. An amount of 18 g glucose corresponds to

(A)  1.8 mole

(B)  1 mole

(C)  0.18 mole

(D)  0.1 mole

Show Answer

56. The number of electrons required to reduce one molecule of oxygen to water during mitochondrial oxidation is

(A)  4

(B)  3

(C)  2

(D)  1

Show Answer

57. Which ONE of the following molecules is derived from pantothenic acid ?

(A)  Thiamine pyrophosphate

(B)  Nicotinamide adenine dinucleotide phosphate

(C)  Flavin adenine dinucleotide phosphate

(D)  Acetyl-CoA

Show Answer

58. Match the disease given in Column I with the principal causal organism in Column II and choose the correct combination.

Colum I                  Column II

(P) AIDS                 (i) HBV

(Q) Syphilis            (ii) Neisseria sp.

(R) Viral hepatitis   (iii) Treponema sp.

(S) Gonorrhoea       (iv) HIV

(A)  P-iv, Q-iii, R-i, S-ii

(B)  P-iv, Q-ii, R-i, S-iii

(C)  P-i, Q-ii, R-iv, S-iii

(D)  P-i, Q-iv, R-ii, S-ii

Show Answer

59. Chromosomes are classified based on the position of centromere. A chromosome having a terminal centromere is called

(A)  metacentric

(B)  telocentric

(C)  sub-metacentric

(D)  acrocentric

Show Answer

60. Which ONE of the following options lists the primary energy source (s) for all forms of life on earth ?

(A)  Light, Inorganic substances

(B)  Inorganic substances, Organic substances

(C)  Light, Organic substances

(D)  N₂, CO₂

Show Answer

Section 5-Part B-Mathematics

61. Let ABCD be a trapezium with parallel sides AB and CD such that the circle S with AB as its diameter touches CD. Further, the circle S passes through the midpoints of the diagonals AC and BD of the trapezium. The smallest angle of the trapezium is

(A)  π/3

(B)  π/4

(C)  π/5

(D)  π/6

Show Answer

62. Let S be the set of all points (a/b, c/d) on the circle with radius 1 centred at (0,0) where a and b are relatively prime integers, c and d are relatively prime integers (that is HCF (a, b) = HCF (c,d) = 1), and the integers b and d are even. Then the set S

(A)  is empty

(B)  has four elements

(C)  has eight elements

(D)  is infinite

Show Answer

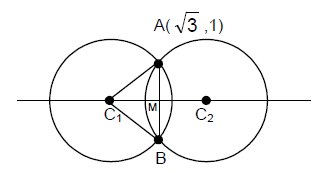
63. Suppose we have two circles of radius 2 each in the plane such that the distance between their centres is 2√ The area of the region common to both circles lies between

(A)  0.5 and 0.6

(B)  0.65 and 0.7

(C)  0.7 and 0.75

(D)  0.8 and 0.9

Show Answer

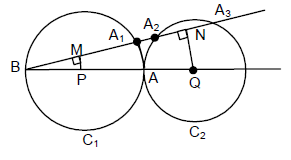
64. Let C₁, C₂ be two circles touching each other externally at the point A and let AB be the diameter of circle C₁. Draw a secant BA₃ to circle C₂, intersecting circle C₁ at a point A₁(≠A), and circle C₂ at points A₂ and A₃ . If BA₁ = 2, BA₂ = 3 and BA₃ = 4, then the radii of circles C₁ and C₂ are respectively

(A) 

(B) 

(C) 

(D) 

Show Answer

65. Let a, b, c, d be real numbers between – 5 and 5 such that

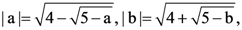
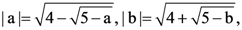
Then the product abcd is

(A)  11

(B)  −11

(C)  121

(D)  −121

Show Answer

Section 6-Part B-Physics

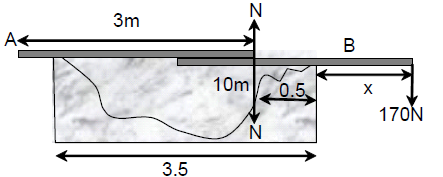
66. Persons A and B are standing on the opposite sides of a 3.5 m wide water stream which they wish to cross. Each one of them has a rigid wooden plank whose mass can be neglected. However, each plank is only slightly longer than 3 m. So they decide to arrange them together as shown in the figure schematically. With (mass 17 kg) standing, the maximum mass of A, who can walk over the plank is close to ,

(A)  17 kg.

(B)  65 kg.

(C)  80 kg.

(D)  105 kg.

Show Answer

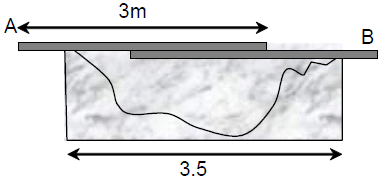
67. Two different liquids of same mass are kept in two identical vessels, which are placed in a freezer that extracts heat from them at the same rate causing each liquid to transform into a solid. The schematic figure below shows the temperature T vs time t plot for the two materials. We denote the specific heat of metrials in the liquid (solid) states to be C_L1 (C_S1) and C_{L 2} (C_S2) respectively.

(A)  C_L1 < C_L2 and C_S1 < C_S2

(B)  C_L1> C_L2 and C_S1 > C_S2

(C)  C_L1 > C_L2 and C_S1 > C_S2

(D)  C_L1 < C_L2 and C_S1 > C_S2

Show Answer

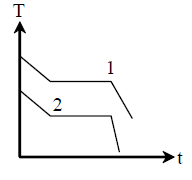
68. A ray of light originates from inside a glass slab and is incident on its inner surface at an angle θ as shown,

In this experiment the location x of the spot where the ray hits the screen is recorded. Which of the following correctly shows the plot of variation of x with the angle θ ?

(A)  A

(B)  B

(C)  C

(D)  D

Show Answer

69. Four identical pendulums are made by made by attaching a small ball of mass 100 g on a 20 cm long thread and suspended from the same point. Now each ball is given charge Q so that balls move away from each other with each thread making an angle of 45° from the vertical. The value of Q is close to

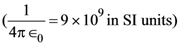
(A)  1μC

(B)  1.5 μC

(C)  2 μC

(D)  2.5 μC

Show Answer

70. Two parallel discs are connected by a rigid rod of length L = 0.5 m centrally. Each disc has a slit oppositely placed as shown in the figure. A beam of neutral atoms are incident on one of the discs axially at different velocities v, while the system is rotated at angular speed of 600 rev/second so that atoms only with a specific velocity emerge at the other end. Calculate the two largest speeds (in meter/second) of the atoms that will emerge at the other end.

(A)  75, 25

(B)  100, 50

(C)  300,100

(D)  600, 200

Show Answer

Section 7 -Part-B chemistry

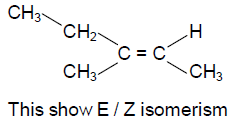
71. Among the following compounds, E/Z isomerism is possible for

(A)  2-methylbut-2-ene

(B)  2-methylbut-1-ene

(C)  3-methylpent-1-ene

(D)  3-methylpent-2-ene

Show Answer

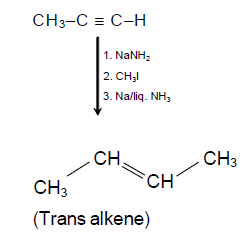
72. In the reaction

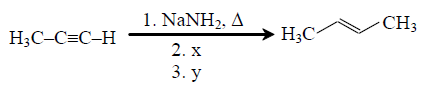
x and y, respectively, are

(A)  x = CH₃OH ; y = Pd/BaSO₄ ,quinoline, H₂

(B)  x = CH₃I ; y = Pd/BaSO₄ ,quinoline, H₂

(C)  x = CH₃I ; y = Na in liq. NH₃

(D)  x = CH₃OH ; y = Na in liq. NH₃

Show Answer

73. Among the following molecules, the one with the largest bond angle at the central atom is

(A)  ClF₃

(B)  POCl­₃

(C)  BCl­₃

(D)  SO₃

Show Answer

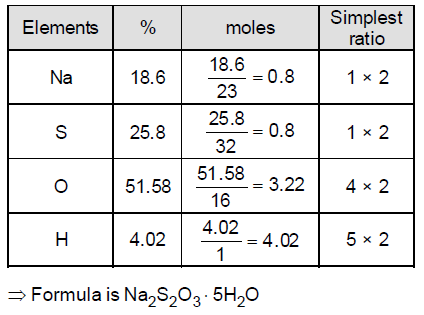
74. A compound has the following composition by weight ; Na = 18.60 %, S = 25.80 %, H = 4.02 % and O = 51.58 % Assuming that all the hydrogen atoms in the compound are part of water of crystallization, the correct molecular formula of the compound is

(A)  Na₂S₂O₃.3H₂O

(B)  Na₂SO₄.5H₂O

(C)  Na₂SO₄.10H₂O

(D)  Na₂S₂O₃.5H₂O

Show Answer

75. X g of ice at 0 °C is added to 340 g of water at 20° C. The final temperature of the resultant mixture is 5 °C. The value of X (in g) is closest to

[Heat of fusion of ice = 333 J/g ; Specific heat of water = 4.184 J/g. K]

(A)  80.4

(B)  52.8

(C)  120.6

(D)  60.3

Show Answer

Section 8-Part B-Biology

76. Considering ABO blood grouping system in humans, during blood transfusion some combinations of blood groups are compatible (√), whereas the others are incompatible (X). Which ONE of the following options is CORRECT ?

(A) 

(B)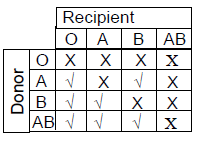 

(C)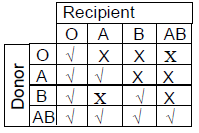 

(D)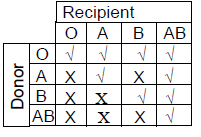 

Show Answer

77. A 25,000 Da protein contains a single binding site for a molecule (ligand), whose molecular weight is 2,500 Da. Assuming high affinity and physiologically irreversible blinding, the amount of the ligand required to occupy all the binding sites in 10 mg protein will be

(A)  0.1 mg

(B)  1 mg

(C)  10 mg

(D)  100 mg

Show Answer

78. In an in vitro tanslation experiment, poly (UC) RNA template produced poly (Ser-Leu), while poly (AG) RNA template produced poly (Arg-Glu) polypeptide. Which ONE of the following options represents correct interpretations of the codons assignments for Ser, Leu, Arg, and Glu.

(A)  Ser – UCU, Leu – CUC, Arg – AGA, Glu – GAG

(B)  Ser – CUC, Leu – GAG, Arg – UCU, Glu – AGA

(C)  Ser – AGA, Leu – UCU, Arg – GAG, Glu – CUC

(D)  Ser – GAG, Leu – AGA, Arg – CUC, Glu – UCU

Show Answer

79. A single bacterium is actively growing in a medium that supports its growth to a number of 100 million. Assuming the division time of the bacterium as 3 hours and the life span of non-dividing bacteria as 5 hours, which ONE of the following represents the maximum number of bacteria that would be present at the end of 15 hour ?

(A)  10

(B)  64

(C)  24

(D)  32

Show Answer

80. A couple has two sons and two daughters. Only one son is colour blind and the rest of the siblings are normal. Assuming colour blindness is sex-linked, which ONE of the following would be the phenotype of the parents ?

(A)  Mother would be colour blind, father would be normal.

(B)  Father would be colour blind, mother would be normal.

(C)  Both the parents would be normal.

(D)  Both the parents would be colour blind.

Show Answer

Latest Govt Job & Exam Updates:

View Full List ...