GATE 2019 General Aptitude (GA) Set-8
Q. 1 – Q. 5 carry one mark each.
1. The fishermen, ________ the flood victims owed their lives, were rewarded by the government.
(A) whom
(B) to which
(C) to whom
(D) that
2. Some students were not involved in the strike.
If the above statement is true, which of the following conclusions is/are logically necessary?
1. Some who were involved in the strike were students.
2. No student was involved in the strike.
3. At least one student was involved in the strike.
4. Some who were not involved in the strike were students.
(A) 1 and 2
(B) 3
(C) 4
(D) 2 and 3
3. The radius as well as the height of a circular cone increases by 10%. The percentage increase in its volume is .
(A) 17.1
(B) 21.0
(C) 33.1
(D) 72.8
4. Five numbers 10, 7, 5, 4 and 2 are to be arranged in a sequence from left to right following the directions given below:
1. No two odd or even numbers are next to each other.
2. The second number from the left is exactly half of the left-most number.
3. The middle number is exactly twice the right-most number.
Which is the second number from the right?
(A) 2
(B) 4
(C) 7
(D) 10
5. Until Iran came along, India had never been in kabaddi.
(A) defeated
(B) defeating
(C) defeat
(D) defeatist
Q. 6 – Q. 10 carry two marks each.
6. Since the last one year, after a 125 basis point reduction in repo rate by the Reserve Bank of India, banking institutions have been making a demand to reduce interest rates on small saving schemes. Finally, the government announced yesterday a reduction in interest rates on small saving schemes to bring them on par with fixed deposit interest rates.
Which one of the following statements can be inferred from the given passage?
(A) Whenever the Reserve Bank of India reduces the repo rate, the interest rates on small saving schemes are also reduced
(B) Interest rates on small saving schemes are always maintained on par with fixed deposit interest rates
(C) The government sometimes takes into consideration the demands of banking institutions before reducing the interest rates on small saving schemes
(D) A reduction in interest rates on small saving schemes follow only after a reduction in repo rate by the Reserve Bank of India
7. In a country of 1400 million population, 70% own mobile phones. Among the mobile phone owners, only 294 million access the Internet. Among these Internet users, only half buy goods from e-commerce portals. What is the percentage of these buyers in the country?
(A) 10.50
(B) 14.70
(C) 15.00
(D) 50.00
8. The nomenclature of Hindustani music has changed over the centuries. Since the medieval period dhrupad styles were identified as baanis. Terms like gayaki and baaj were used to refer to vocal and instrumental styles, respectively. With the institutionalization of music education the term gharana became acceptable. Gharana originally referred to hereditary musicians from a particular lineage, including disciples and grand disciples.
Which one of the following pairings is NOT correct?
(A) dhrupad, baani
(B) gayaki, vocal
(C) baaj, institution
(D) gharana, lineage
9. Two trains started at 7AM from the same point. The first train travelled north at a speed of 80km/h and the second train travelled south at a speed of 100 km/h. The time at which they were 540 km apart is AM.
(A) 9
(B) 10
(C) 11
(D) 11.30
10. “I read somewhere that in ancient times the prestige of a kingdom depended upon the number of taxes that it was able to levy on its people. It was very much like the prestige of a head-hunter in his own community.”
Based on the paragraph above, the prestige of a head-hunter depended upon
(A) the prestige of the kingdom
(B) the prestige of the heads
(C) the number of taxes he could levy
(D) the number of heads he could gather
Statistics
Q.1 – Q.25 carry one mark each.
1.  is equal to
is equal to
(A) e/3
(B) 5/6
(C) 3/4
(D) π/4
2. Let ![]() The line integral
The line integral ![]() where C is the triangle with vertices (0,0,0), (5,0,0) and (5,5,0) traversed in that order is
where C is the triangle with vertices (0,0,0), (5,0,0) and (5,5,0) traversed in that order is
(A) -25
(B) 25
(C) 50
(D) 5
3. Let {1,2,3,4} represent the outcomes of a random experiment, and 𝑃({1}) = 𝑃({2}) = 𝑃({3}) = 𝑃({4}) = 1/4. Suppose that 𝐴1 = {1,2}, 𝐴2 = {2,3}, 𝐴3 = {3,4}, and 𝐴4 = {1,2,3}. Then which of the following statements is true?
(A) 𝐴1 and 𝐴2 are not independent.
(B) 𝐴3 and 𝐴4 are independent.
(C) 𝐴1 and 𝐴4 are not independent.
(D) 𝐴2 and 𝐴4 are independent.
4. A fair die is rolled two times independently. Given that the outcome on the first roll is 1, the expected value of the sum of the two outcomes is
(A) 4
(B) 4.5
(C) 3
(D) 5.5
5. The dimension of the vector space of 7 × 7 real symmetric matrices with trace zero and the sum of the off-diagonal elements zero is
(A) 47
(B) 28
(C) 27
(D) 26
6. Let 𝐴 be a 6 × 6 complex matrix with 𝐴3 ≠ 𝟎 and 𝐴4 = 𝟎. Then the number of Jordan blocks of 𝐴 is
(A) 1 or 6
(B) 2 or 3
(C) 4
(D) 5
7. Let 𝑋1, … , 𝑋𝑛 be a random sample from uniform distribution defined over (0, 𝜃), where 𝜃 > 0 and 𝑛 ≥ 2. Let 𝑋(1) = min{𝑋1, … , 𝑋𝑛} and 𝑋(𝑛) = max{𝑋1, … , 𝑋𝑛}. Then the covariance between 𝑋(𝑛) and 𝑋(1)/ 𝑋(𝑛) is
(A) 0
(B) 𝑛(𝑛 + 1)𝜃
(C) 𝑛 𝜃
(D) 𝑛2(𝑛 + 1)𝜃
8. Let 𝑋1, … , 𝑋𝑛 be a random sample drawn from a population with probability density function 𝑓(𝑥; 𝜃) = 𝜃𝑥𝜃−1, 0 ≤ 𝑥 ≤ 1, 𝜃 > 0. Then the maximum likelihood estimator of 𝜃 is




9. Let 𝑌𝑖 = 𝛽0 + 𝛽1𝑥1𝑖 + 𝛽2𝑥2𝑖 + 𝜖𝑖, for 𝑖 = 1, … ,10, where 𝑥1𝑖′s and 𝑥2𝑖′s are fixed covariates, and 𝜖𝑖′s are uncorrelated random variables with mean 0 and unknown variance 𝜎2. Here 𝛽0, 𝛽1 and 𝛽2 are unknown parameters. Further, define ![]()
![]() is the unbiased least squares estimator of (𝛽0, 𝛽1, 𝛽2). Then an unbiased estimator of 𝜎2 is
is the unbiased least squares estimator of (𝛽0, 𝛽1, 𝛽2). Then an unbiased estimator of 𝜎2 is




10. For 𝑖 = 1,2,3, let 𝑌𝑖 = 𝛼 + 𝛽𝑥𝑖 + 𝜖𝑖, where 𝑥𝑖′s are fixed covariates, and 𝜖𝑖′s are independent and identically distributed standard normal random variables. Here, 𝛼 and 𝛽 are unknown parameters. Given the following observations,

the best linear unbiased estimate of 𝛼 + 𝛽 is equal to
(A) 1.5
(B) 1
(C) 1.8
(D) 2.1
11. Consider a discrete time Markov chain on the state space {1,2,3} with one-step transition probability matrix  Which of the following statements is true?
Which of the following statements is true?
(A) States 1, 3 are recurrent and state 2 is transient.
(B) State 3 is recurrent and states 1, 2 are transient.
(C) States 1, 2, 3 are recurrent.
(D) States 1, 2 are recurrent and state 3 is transient.
12. The minimal polynomial of the matrix  is
is
(A) (𝑥 − 1)(𝑥 − 2)
(B) (𝑥 − 1)2(𝑥 − 2)
(C) (𝑥 − 1)(𝑥 − 2)2
(D) (𝑥 − 1)2(𝑥 − 2)2
13. Let (𝑋1, 𝑋2, 𝑋3) be a trivariate normal random vector with mean vector (−3, 1,4) and variance-covariance matrix  Which of the following statements are true?
Which of the following statements are true?
(i) 𝑋2 and 𝑋3 are independent.
(ii) 𝑋1 + 𝑋3 and 𝑋2 are independent.
(iii) (𝑋2 , 𝑋3) and 𝑋1 are independent.
(iv) 1/2 (𝑋2 + 𝑋3) and 𝑋1 are independent.2
(A) (i) and (iii)
(B) (ii) and (iii)
(C) (i) and (iv)
(D) (iii) and (iv)
14. A 23 factorial experiment with factors 𝐴, 𝐵 and 𝐶 is arranged in two blocks of four plots each as follows: (Below (1) denotes the treatment in which 𝐴, 𝐵 and 𝐶 are at the lower level, ac denotes the treatment in which 𝐴 and 𝐶 are at the higher level and 𝐵 is at the lower level and so on.)

The treatment contrast that is confounded with the blocks is
(A) 𝐵𝐶
(B) 𝐴𝐶
(C) 𝐴𝐵
(D) 𝐴𝐵𝐶
15. Consider a fixed effects two-way analysis of variance model 𝑌𝑖𝑗𝑘 = 𝜇 + 𝛼𝑖 + 𝛽𝑗 + 𝛾𝑖𝑗 + 𝜖𝑖𝑗𝑘, where 𝑖 = 1, … , 𝑎; 𝑗 = 1, … , 𝑏 ; 𝑘 = 1, … , 𝑟, and 𝜖𝑖𝑗𝑘′s are independent and identically distributed normal random variables with zero mean and constant variance. Then the degrees of freedom available to estimate the error variance is zero when
(A) 𝑎 = 1
(B) 𝑏 = 1
(C) 𝑟 = 1
(D) None of the above.
16. For 𝑘 = 1,2, … ,10, let the probability density function of the random variable 𝑋𝑘 be

Then  is equal to …….
is equal to …….
17. The probability density function of the random vector (𝑋, 𝑌) is given by

Then the value of 𝑐 is equal to………
18. Let { 𝑋𝑛}𝑛≥1 be a sequence of independent and identically distributed normal random variables with mean 4 and variance 1. Then ![]() is equal to ……
is equal to ……
19. Let (𝑋1, 𝑋2) be a random vector following bivariate normal distribution with mean vector (0, 0), Variance(𝑋1) = Variance(𝑋2) = 1 and correlation coefficient 𝜌, where |𝜌| < 1. Then 𝑃(𝑋1 + 𝑋2 > 0) is equal to …………
20. Let 𝑋1, … , 𝑋𝑛 be a random sample from normal distribution with mean 𝜇 and variance 1. Let ϕ be the cumulative distribution function of the standard normal distribution. Given ϕ(1.96) = 0.975, the minimum sample size required such that the length of the 95% confidence interval for 𝜇 does NOT exceed 2 is …………..
21. Let 𝑋 be a random variable with probability density function 𝑓(𝑥; 𝜃) = 𝜃𝑒−𝜃𝑥, where 𝑥 ≥ 0 and 𝜃 > 0. To test 𝐻0: 𝜃 = 1 against 𝐻1: 𝜃 > 1, the following test is used:
Reject 𝐻0 if and only if 𝑋 > log𝑒20.
Then the size of the test is ……….
22. Let {𝑋𝑛}𝑛≥0 be a discrete time Markov chain on the state space {1,2,3} with one-step transition probability matrix

and initial distribution 𝑃(𝑋0 = 1) = 0.5, 𝑃(𝑋0 = 2) = 0.2, 𝑃(𝑋0 = 3) = 0.3 . Then 𝑃(𝑋1 = 2, 𝑋2 = 3, 𝑋3 = 1) (rounded off to three decimal places) is equal to …..
23. Let 𝑓 be a continuous and positive real valued function on [0, 1]. Then ![]() is equal to …..
is equal to …..
24. A random sample of size 100 is classified into 10 class intervals covering all the data points. To test whether the data comes from a normal population with unknown mean and unknown variance, the chi-squared goodness of fit test is used. The degrees of freedom of the test statistic is equal to ………
25. For 𝑖 = 1,2,3,4, let 𝑌𝑖 = 𝛼 + 𝛽𝑥𝑖 + 𝜖𝑖 where 𝑥𝑖′s are fixed covariates and 𝜖𝑖′s are uncorrelated random variables with mean 0 and variance 3. Here, 𝛼 and 𝛽 are unknown parameters. Given the following observations,

the variance of the least squares estimator of 𝛽 is equal to …….
Q.26 – Q. 55 carry two marks each.
26. Let ![]() Then, for |𝑥| < 1, the series
Then, for |𝑥| < 1, the series ![]() converges to
converges to




27. Let {𝑋𝑘}𝑘≥1 be a sequence of independent and identically distributed Bernoulli random variables with success probability 𝑝 ∈ (0,1). Then, as 𝑛 → ∞,

converges almost surely to
(A) p
(B) 1/1 – p
(C) 1 – p/p
(D) 1
28. Let 𝑋 and 𝑌 be two independent random variables with 𝜒2m and 𝜒2n distributions, respectively, where 𝑚 and 𝑛 are positive integers. Then which of the following statements is true?
(A) For 𝑚 < 𝑛, 𝑃(𝑋 > 𝑎) ≥ 𝑃(𝑌 > 𝑎) for all 𝑎 ∈ ℝ.
(B) For 𝑚 > 𝑛, 𝑃(𝑋 > 𝑎) ≥ 𝑃(𝑌 > 𝑎) for all 𝑎 ∈ ℝ.
(C) For 𝑚 < 𝑛, 𝑃(𝑋 > 𝑎) = 𝑃(𝑌 > 𝑎) for all 𝑎 ∈ ℝ.
(D) None of the above.
29. The matrix  is diagonalizable when (𝑥, 𝑦, 𝑧) equals
is diagonalizable when (𝑥, 𝑦, 𝑧) equals
(A) (0,0,1)
(B) (1,1,0)
(C) (√2, √2, 2)
(D) (√2, √2, √2)
30. Suppose that 𝑃1 and 𝑃2 are two populations with equal prior probabilities having bivariate normal distributions with mean vectors (2, 3) and (1, 1), respectively. The variance- covariance matrix of both the distributions is the identity matrix. Let 𝑧1 = (2.5, 2) and 𝑧2 = (2, 1.5) be two new observations. According to Fisher’s linear discriminant rule,
(A) 𝑧1 is assigned to 𝑃1, and 𝑧2 is assigned to 𝑃2.
(B) 𝑧1 is assigned to 𝑃2, and 𝑧2 is assigned to 𝑃1.
(C) 𝑧1 is assigned to 𝑃1, and 𝑧2 is assigned to 𝑃1.
(D) 𝑧1 is assigned to 𝑃2, and 𝑧2 is assigned to 𝑃2.
31. Let 𝑋1, … , 𝑋𝑛 be a random sample from a population having probability density function ![]() Then the method of moments estimator of 𝜃 is
Then the method of moments estimator of 𝜃 is




32. Let 𝑋 be a normal random variable having mean 𝜃 and variance 1, where 1 ≤ 𝜃 ≤ 10. Then 𝑋 is
(A) sufficient but not complete.
(B) the maximum likelihood estimator of 𝜃.
(C) the uniformly minimum variance unbiased estimator of 𝜃.
(D) complete and ancillary.
33. Let {𝑋𝑛}𝑛≥1 be a sequence of independent and identically distributed random variables with mean 𝜃 and variance 𝜃, where 𝜃 > 0. Then ![]() is a consistent estimator of
is a consistent estimator of
(A) 1/1+θ
(B) 1+ θ/θ
(C) 1/θ
(D) θ/1+θ
34. Let 𝑋1, … , 𝑋10 be a random sample from a population with probability density function

Then the maximum likelihood estimator of 𝜃
(A) does not exist.
(B) is not unique.
(C) is the sample mean.
(D) is the smallest observation.
35. Consider the model 𝑌𝑖 = 𝛽 + 𝜖𝑖, where 𝜖𝑖′s are independent normal random variables with zero mean and known variance 𝜎i2 > 0, for 𝑖 = 1, … , 𝑛. Then the best linear unbiased estimator of the unknown parameter 𝛽 is




36. Let (𝑋, 𝑌) be a bivariate random vector with probability density function

Then the regression of 𝑌 on 𝑋 is given by
(A) 𝑋 + 1
(B) 𝑋/2
(C) 𝑌/2
(D) 𝑌 + 1
37. Consider a discrete time Markov chain on the state space {1, 2} with one-step transition probability matrix






38. Let (𝑋1, 𝑋2) be a random vector with variance-covariance matrix ![]() The two principal components are
The two principal components are
(A) 𝑋1 and 𝑋2
(B) −𝑋1 and 𝑋2
(C) 𝑋1 and −𝑋2
(D) 𝑋1 + 𝑋2 and 𝑋2
39. Consider the objects {1,2,3,4} with the distance matrix

Applying the single-linkage hierarchical procedure twice, the two clusters that result are
(A) {2,3} and {1,4}
(B) {1,2,3} and {4}
(C) {1,3,4} and {2}
(D) {2,3,4} and {1}
40. The maximum likelihood estimates of the mean vector and the variance-covariance matrix of a bivariate normal distribution based on the realization  of a random sample of size 3, are given by
of a random sample of size 3, are given by




41. Consider a fixed effects one-way analysis of variance model 𝑌𝑖𝑗 = 𝜇 + 𝜏𝑖 + 𝜖𝑖𝑗, for 𝑖 = 1, … , 𝑎, 𝑗 = 1, … , 𝑟, and 𝜖𝑖𝑗′s are independent and identically distributed normal random variables with mean zero and variance 𝜎2. Here, 𝑟 and 𝑎 are positive integers.
Let ![]() is the least squares estimator for
is the least squares estimator for
(A) μ + τi/2
(B) τi
(C) μ + τi
(D) μ
42. Let 𝐴 be a 𝑛 × 𝑛 positive semi-definite matrix with eigenvalues 𝜆1 ≥ ⋯ ≥ 𝜆𝑛, and with 𝛼 as the maximum diagonal entry. We can find a vector 𝑥 such that 𝑥𝑡𝑥 = 1, where 𝑡 denotes the transpose, and
(A) 𝑥𝑡𝐴 𝑥 > 𝜆1
(B) 𝑥𝑡𝐴𝑥 < 𝜆𝑛
(C) 𝜆𝑛 ≤ 𝑥𝑡𝐴 𝑥 ≤ 𝜆1
(D) 𝑥𝑡𝐴 𝑥 > 𝑛 𝛼
43. Let 𝑋 be a random variable with uniform distribution on the interval (−1,1) and 𝑌 = (𝑋 + 1)2. Then the probability density function 𝑓(𝑦) of 𝑌, over the interval (0,4), is
(A) 3√𝑦/16
(B) 1/4 √𝑦
(C) 1/6 √𝑦
(D) 1/√𝑦
44. Let 𝑆 be the solid whose base is the region in the 𝑥𝑦-plane bounded by the curves 𝑦 = 𝑥2 and 𝑦 = 8 − 𝑥2, and whose cross-sections perpendicular to the 𝑥-axis are squares. Then the volume of 𝑆 (rounded off to two decimal places) is ………….
45. Consider the trinomial distribution with the probability mass function ![]() 𝑥 + 𝑦 ≤ 7.
𝑥 + 𝑦 ≤ 7.
Then 𝐸(𝑌|𝑋 = 3) is equal to ……
46. Let 𝑌𝑖 = 𝛼 + 𝛽𝑥𝑖 + 𝜖𝑖, where 𝑖 = 1, 2, 3, 4, 𝑥𝑖′s are fixed covariates and 𝜖𝑖′s are independent and identically distributed standard normal random variables. Here, 𝛼 and 𝛽 are unknown parameters. Let Φ be the cumulative distribution function of the standard normal distribution and Φ(1.96) = 0.975. Given the following observations,

the length (rounded off to two decimal places) of the shortest 95% confidence interval for 𝛽 based on its least squares estimator is equal to ……….
47. Consider a discrete time Markov chain on the state space {1,2,3} with one-step transition probability matrix  Then the period of the Markov chain is …………
Then the period of the Markov chain is …………
48. Suppose customers arrive at an ATM facility according to a Poisson process with rate 5 customers per hour. The probability (rounded off to two decimal places) that no customer arrives at the ATM facility from 1:00 pm to 1:18 pm is ……….
49. Let 𝑋 be a random variable with characteristic function 𝜙𝑋(⋅) such that 𝜙𝑋(2 𝜋) = 1. Let ℤ denote the set of integers. Then 𝑃(𝑋 ∈ ℤ) is equal to ……..
50. Let 𝑋1 be a random sample of size 1 from uniform distribution over (𝜃, 𝜃2), where 𝜃 > 1. To test 𝐻0: 𝜃 = 2 against 𝐻1: 𝜃 = 3, reject 𝐻0 if and only if 𝑋1 > 3.5 . Let 𝛼 and 𝛽 be the size and the power, respectively, of this test. Then 𝛼 + 𝛽 (rounded off to two decimal places) is equal to ………
51. Let 𝑌𝑖 = 𝛽0 + 𝛽1𝑥𝑖 + 𝜖𝑖, 𝑖 = 1, … , 𝑛, where 𝑥𝑖′s are fixed covariates, and 𝜖𝑖′s are uncorrelated random variables with mean zero and constant variance. Suppose that ![]()
![]() are the least squares estimators of the unknown parameters respectively. If
are the least squares estimators of the unknown parameters respectively. If  then the correlation between
then the correlation between ![]() is equal to ……..
is equal to ……..
52. Let 𝑓: ℝ → ℝ be defined by 𝑓(𝑥) = (3𝑥2 + 4) cos 𝑥. Then ![]() is equal to ……
is equal to ……
53. The maximum value of (𝑥 − 1)2 + (𝑦 − 2)2 subject to the constraint 𝑥2 + 𝑦2 ≤ 45 is equal to……
54. Let 𝑋1, ……… , 𝑋10 be independent and identically distributed normal random variables with mean 0 and variance 2. Then ![]() is equal to ………..
is equal to ………..
55. Let 𝐼 be the 4 × 4 identity matrix and 𝑣 = (1, 2, 3, 4)𝑡, where 𝑡 denotes the transpose. Then the determinant of 𝐼 + 𝑣𝑣𝑡 is equal to ………..
 z = 1 – 4i with
z = 1 – 4i with is
is







 , the Laplace transform of t cosh t is
, the Laplace transform of t cosh t is



 is
is

















 the unit vector along the axis of rotation is
the unit vector along the axis of rotation is






























































 is____(round off to 2 decimal places).
is____(round off to 2 decimal places).






































 from (0,0) to (2,2) in the xy plane is _______.
from (0,0) to (2,2) in the xy plane is _______.

 where K[N ] has the dimension of atm−(1/2).
where K[N ] has the dimension of atm−(1/2).

















 is orthogonal. The value of α, β and γ respectively are
is orthogonal. The value of α, β and γ respectively are

























 is equal to
is equal to












































 is the unit vector in the y direction, t (> 0) is in seconds, and x and y are in meters. The magnitude of total acceleration at the point (x, y) = (1, 1) at t = 2 s is _______ m/s2.
is the unit vector in the y direction, t (> 0) is in seconds, and x and y are in meters. The magnitude of total acceleration at the point (x, y) = (1, 1) at t = 2 s is _______ m/s2.






















 If the radius of convergence of
If the radius of convergence of  then which one of the following statements is necessarily TRUE?
then which one of the following statements is necessarily TRUE?
 converges to 0.
converges to 0. converges to 0.
converges to 0. (the set of all natural numbers).
(the set of all natural numbers).







 is summable for all i ∈ ℕ, and (y1, y2 …) ∈ ℓ1, where
is summable for all i ∈ ℕ, and (y1, y2 …) ∈ ℓ1, where 








 is
is


 is equal to _______
is equal to _______



 is equal to _______(round off to 2 places of decimal).
is equal to _______(round off to 2 places of decimal).

































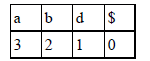
 of a sample whose
of a sample whose 









































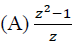
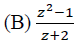


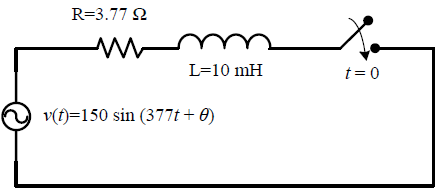

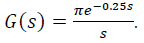


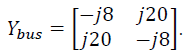
 is ______.
is ______. are the row vectors. Consider the following statements:
are the row vectors. Consider the following statements:


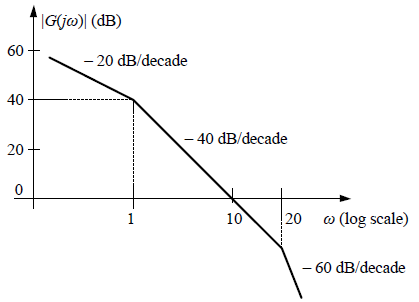


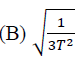


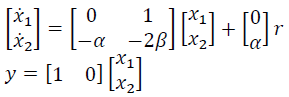




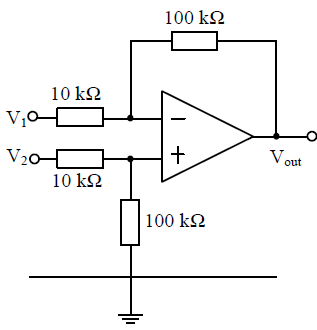

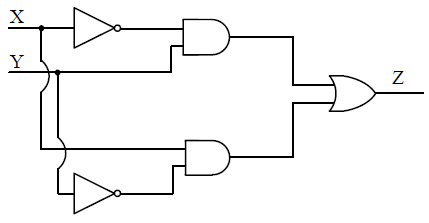


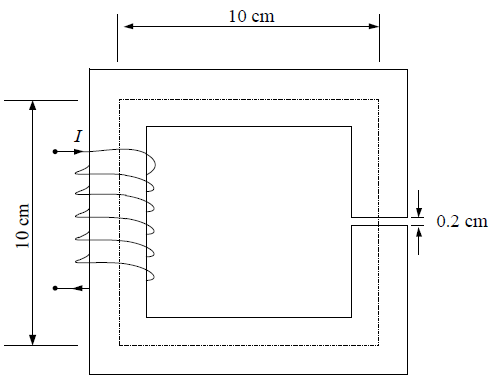


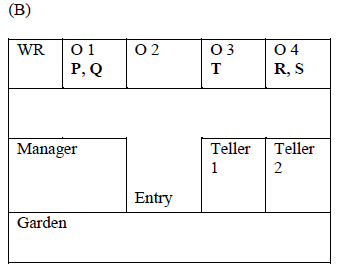





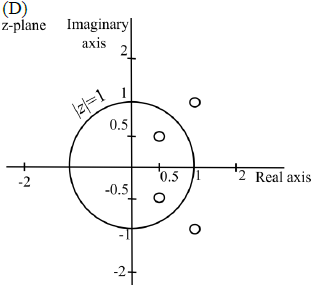

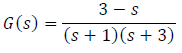





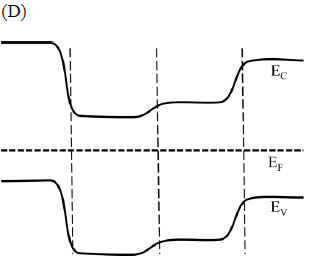
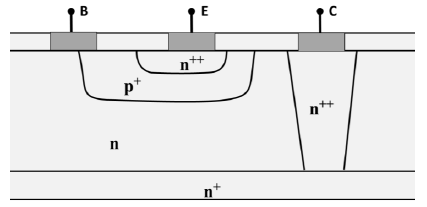







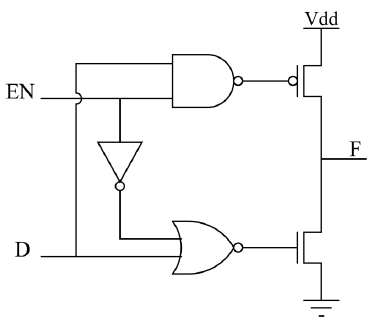




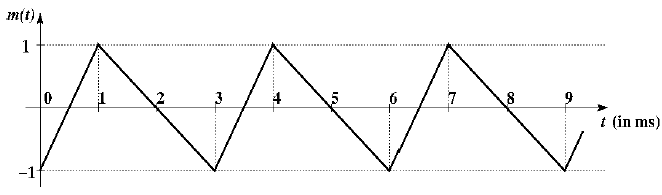
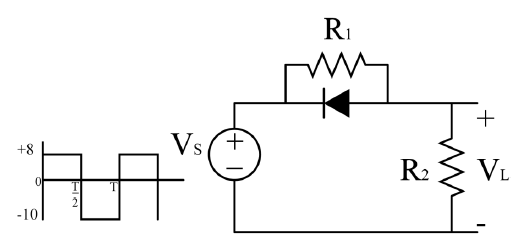
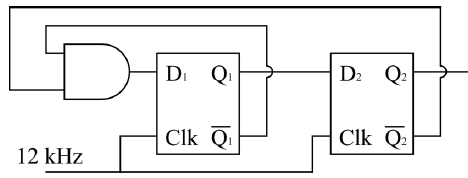



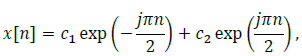





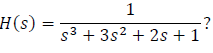











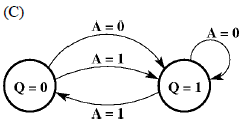



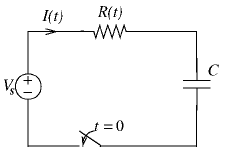







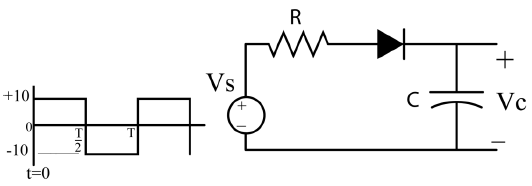









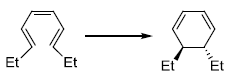
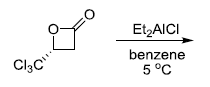


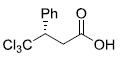

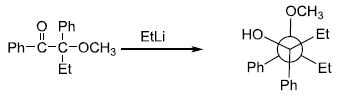

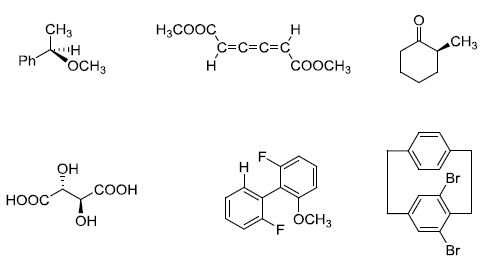



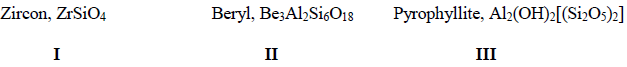




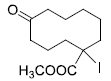
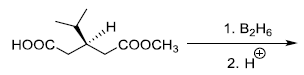
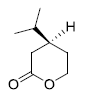



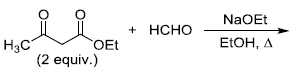




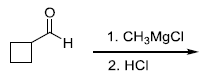


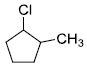
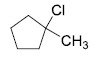










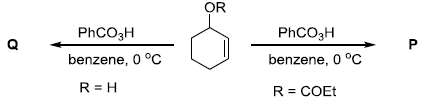







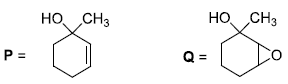
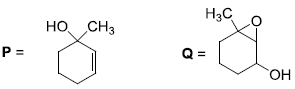

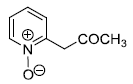
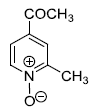
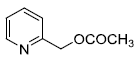












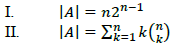













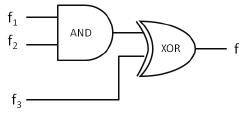


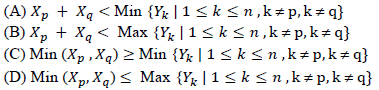







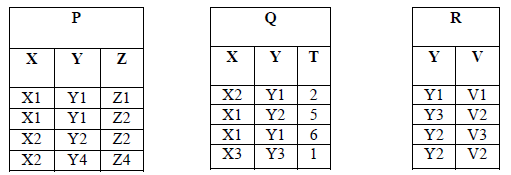
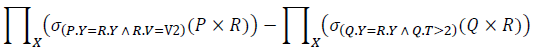
 is
is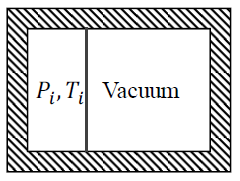







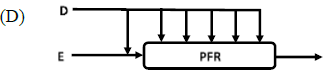







 is ______ (rounded off to one decimal place).
is ______ (rounded off to one decimal place).
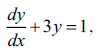 subject to the initial condition
subject to the initial condition










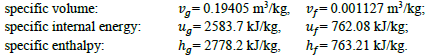
 , and the constants are provided below:
, and the constants are provided below:
 where Ti, in and Ti, out refer to the temperature of the ith stream (i = A, B) at the inlet and exit, respectively. The mass flow rate of stream A (in kg/s), is _______ (rounded off to two decimal places).
where Ti, in and Ti, out refer to the temperature of the ith stream (i = A, B) at the inlet and exit, respectively. The mass flow rate of stream A (in kg/s), is _______ (rounded off to two decimal places).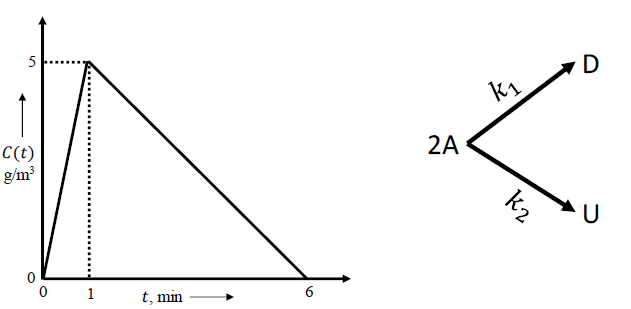






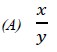





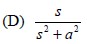
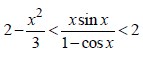



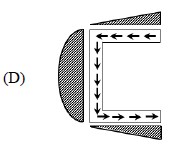
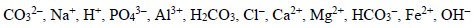



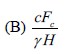



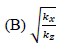




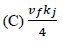







 is
is 

















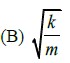
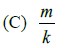

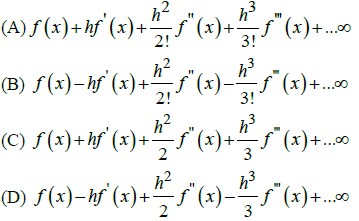









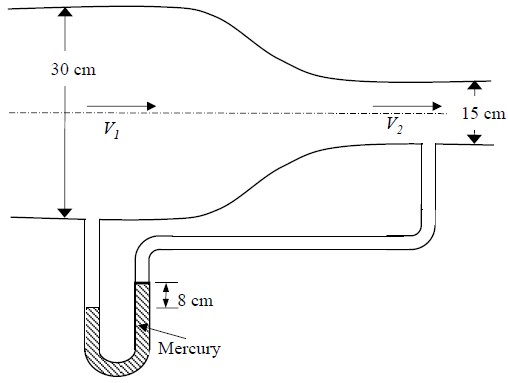

 is
is
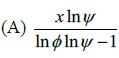




 the vertical reaction at the support S will become zero when β is equal to
the vertical reaction at the support S will become zero when β is equal to
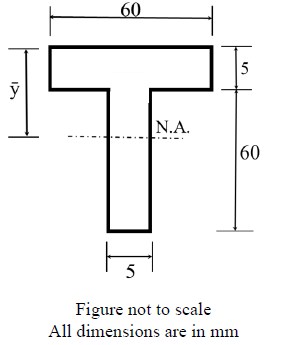
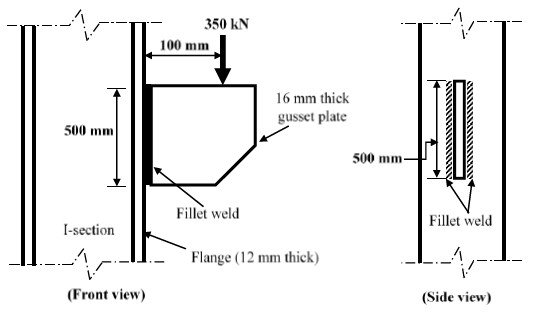


 Given the values of y(1) = 0 and y(2) = 2, the value of y(3) (round off to 1 decimal place), is ______
Given the values of y(1) = 0 and y(2) = 2, the value of y(3) (round off to 1 decimal place), is ______

