JEE MAIN (AIEEE) Past Exam Paper-2003
Mathematics
1. A function f from the set of natural numbers to integers defined by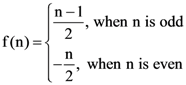 
is
(1) one-one but not onto
(2) onto but not one-one
(3) one-one and onto both
(4) neither one-one nor onto
2. Let z1 and z2 be two roots of the equation z2 + az + b = 0, z being complex. Further, assume that the origin, z1 and z2 form an equilateral triangle. Then
(1) a2 = b
(2) a2 = 2b
(3) a2 = 3b
(4) a2 = 4b
3. If z and ω are two non-zero complex numbers such that |zω| = 1, and arg(z) – arg(ω) = π/2, then 
is equal to
(1) 1
(2) −1
(3) i
(4) −i
4. 
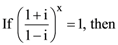
(1) x = 4 n, where n is any positive integer
(2) x = 2n, where n is any positive integer
(3) x = 4n + 1, where n is any positive integer
(4) x = 2n + 1, where n is any positive integer
5. If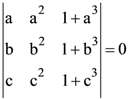 
and vectors (1, a, a2), (1, b, b2) and (1, c, c2) are non-coplanar, then the product abc equals
(1) 2
(2) −1
(3) 1
(4) 0
6. If the system of linear equations
x + 2 ay + az = 0,
x + 3 by + bz = 0
and x + 4 cy + cz = 0
has a non-zero solution, then a, b, c
(1) are in AP
(2) are in GP
(3) are in HP
(4) satisfy a + 2b + 3c = 0
7. If the sum of the roots of the quadratic equation ax2 + bx + c = 0 is equal to the sum of the squares of their reciprocals, then a/c, b/a and c/b are in
(1) AP
(2) GP
(3) HP
(4) arithmetic-geometric progression
8. The number of the real solutions of the equation x2 – 3|x| + 2 = 0 is
(1) 2
(2) 4
(3) 1
(4) 3
9. The value of ‘a’ for which one root of the quadratic equation
(a2 – 5a + 3)x2 + (3a – 1)x + 2 = 0 is twice as large as the other, is
(1) 2/3
(2) −2/3
(3) 1/3
(4) −1/3
10. If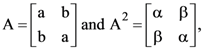 
then
(1) α2 = a2 + b2, β = ab
(2) α = a2 + b2, β = 2ab
(3) α = a2 + b2, β = a2 – b2
(4) α = 2ab, β = a2 + b2
11. A student is to answer 10 out of 13 questions in an examination such that he must choose at least 4 from the first five questions. The number of choices available to him is
(1) 140
(2) 196
(3) 280
(4) 346
12. The number of ways in which 6 men and 5 women can dine at a round table, if not tow women are to sit together, is given by
(1) 6! × 5!
(2) 30
(3) 5! × 4!
(4) 7! × 5!
13. If 1, ω, ω2 are the cube roots of unity, then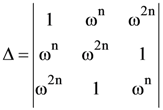 
is equal to
(1) 0
(2) 1
(3) ω
(4) ω2
14. If nCr denotes the number of combinations of n things taken r at a time, then the expression nCr+1+ nCr−1+ 2 × nCr equals
(1) n+2Cr
(2) n+2Cr+1
(3) n+1Cr
(4) n+1Cr+1
15. The number of integral terms in the expansion of 
is
(1) 32
(2) 33
(3) 34
(4) 35
16. If x is positive, the first negative term in the expansion of (1 + x)27/5 is
(1) 7th term
(2) 5th term
(3) 8th term
(4) 6th term
17. The sum of the series 
upto ∞ is equal to
(1) 2 loge 2
(2) loge 2 – 1
(3) loge 2
(4) loge (4/e)
18. Let f(x) be a polynomial function of second degree. If f(1) = f(−1) and a, b, c are in AP, then f'(a), f'(b) and f'(c) are in
(1) AP
(2) GP
(3) HP
(4) arithmetic-geometric progression
19. If x1, x2, x3 and y1, y2, y3 are both in GP with the same common ratio, then the points (x1, y1), (x2, y2) and (x3, y3)
(1) lie on a straight line
(2) lie on an ellipse
(3) lie on a circle
(4) are vertices of a triangle
20. The sum of the radii of inscribed and circumscribed circles for an n sided regular polygon of side a, is
(1) a cot (π/n)
(2) (a/2) cot (π/2n)
(3) a cot (π/2n)
(4) (a/4) cot (π/2n)
21. If in a ∆ABC 
then the sides a, b and c
(1) are in AP
(2) are in GP
(3) are in HP
(4) satisfy a + b = c
22. In a ∆ABC, medians AD and BE are drawn. If AD = 4, ∠DAB = π/6 and ∠ABE = π/3, then the area of the ∆ ABC is
(1) 8/3
(2) 16/3
(3) 32/3√3
(4) 64/3
23. The trigonometric equation sin−1x = 2sin−1 a, has a solution for
(1) 
(2) all real values of a
(3) 
(4) 
24. The upper 3/4th portion of a vertical pole subtends an angle tan−1 (3/5) at a point in the horizontal plane through its foot and at a distance 40 m from the foot. A possible height of the vertical pole is
(1) 20 m
(2) 40 m
(3) 60 m
(4) 80 m
25. The real number x when added to its inverse gives the minimum sum at x equals
(1) 2
(2) 1
(3) −1
(4) −2
26. If f:R→R satisfies f(x + y) = f(x) + f(y), for all x, y ∈ R and f(1) = 7, then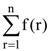 
is
(1) 7n/2
(2) 
(3) 7n(n+1)
(4) 
27. If f(x) = xn, then the value of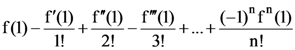 
is
(1) 2n
(2) 2n – 1
(3) 0
(4) 1
28. Domain of definition of the function 
is
(1) (1, 2)
(2) (−1, 0) ∪ (1, 2)
(3) (1, 2) ∪ (2, ∞)
(4) (−1, 0) ∪ (1, 2) ∪ (2, ∞)
29. 
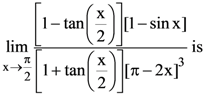
(1) 1/8
(2) 0
(3) 1/32
(4) ∞
30. If 
then value of k is
(1) 0
(2) −1/3
(3) 2/3
(4) −2/3
31. Let f(a) = g(a) = k and their nth derivatives fn (a), gn (a) exist and are not equal for some n. Further, if
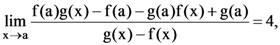
then the value of k is equal to
(1) 4
(2) 2
(3) 1
(4) 0
32. The function 
is
(1) an even function
(2) an odd function
(3) a periodic function
(4) neither an even nor an odd function
33. 
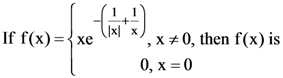
(1) continuous as well as differentiable for all x
(2) continuous for all x but not differentiable at x = 0
(3) neither differentiable nor continuous at x = 0
(4) discontinuous everywhere
34. If the function f(x) = 2x3 – 9ax2 + 12a2x + 1, where a > 0, attains its maximum and minimum at p and q respectively such that p2 = q, then a equals
(1) 3
(2) 1
(3) 2
(4) 1/2
35. If f(y) = ey, g(y) = y; y > 0 and 
then
(1) F(t) = 1 – e−t(1 + t)
(2) F(t) = et – (1 + t)
(3) F(t) = tet
(4) F(t) = te−t
36. If f(a + b – x) = f(x), then 
is equal to
(1) 
(2) 
(3) 
(4) 
37. The value of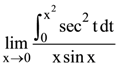 
is
(1) 3
(2) 2
(3) 1
(4) −1
38. The value of the integral 
is
(1) 
(2) 
(3) 
(4) 
39. 
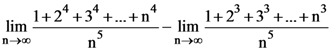is
(1) 1/30
(2) 0
(3) 1/4
(4) 1/5
40. Let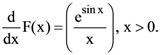 
If 
then one of the possible values of k, is
(1) 15
(2) 16
(3) 63
(4) 64
41. The area of the region bounded by the curves y = |x – 1| and y = 3 – |x| is
(1) 2 sq unit
(2) 3 sq unit
(3) 4 sq unit
(4) 6 sq unit
42. Let f(x) be function satisfying f'(x) = f(x) with f(0) = 1 and g(x) be a function that satisfies f(x) + g(x) = x2. Then, the value of the integral 
is
(1) 
(2) 
(3) 
(4) 
43. The degree and order of the differential equation of the family of all parabolas whose axis is x-axis, are respectively
(1) 2, 1
(2) 1, 2
(3) 3, 2
(4) 2, 3
44. The solution of the differential equation 
is
(1) 
(2) 
(3) 
(4) 
45. If the equation of the locus of a point equidistant from the points (a1, b1) and (a2, b2) is (a1 – a2) x + (b1 – b2)y + c = 0, then the value of ‘c’ is
(1) 
(2) 
(3) 
(4) 
46. Locus of centroid of the triangle whose vertices are (a cos t, a sin t), (b sin t, −b cos t) and (1, 0), where t is parameter, is
(1) (3x – 1)2 + (3y)2 = a2 – b2
(2) (3x – 1)2 + (3y)2 = a2 + b2
(3) (3x + 1)2 + (3y)2 = a2 + b2
(4) (3x + 1)2 + (3y)2 = a2 – b2
47. If the pair straight lines x2 – 2pxy – y2 = 0 and x2 – 2qxy – y2 = 0 be such that each pair bisects the angle between the other pair, then
(1) p = q
(2) p = −q
(3) pq = 1
(4) pq = −1
48. A square of side a lies above the x-axis and has one vertex at the origin. The side passing through the origin makes an angle α(0 < α < π/4) with the positive direction of x-axis. The equation of its diagonal not passing through the origin is
(1) y(cos α – sin α) – x(sin α – cos α) = a
(2) y(cos α + sin α) + x( sin α – cos α) = a
(3) y(cos α + sin α) + x(sin α + cos α) = a
(4) y(cos α + sin α) + x(cos α – sin α) = a
49. If the two circles (x – 1)2 + (y – 3)2 =r2 and x2 + y2 – 8x + 2y + 8 = 0 intersect in two distinct points, then
(1) 2 < r < 8
(2) r < 2
(3) r = 2
(4) r > 2
50. The lines 2x – 3y = 5 and 3x – 4y = 7 are diameters of a circles having area as 154 sq unit. Then, the equation of the circle is
(1) x2 + y2+ 2x – 2y = 62
(2) x2 + y2 + 2x – 2y = 47
(3) x2 + y2 − 2x + 2y = 47
(4) x2 + y2 − 2x + 2y = 62
51. The normal at the point 
on a parabola meets the parabola again in the point 
then
(1) 
(2) 
(3) 
(4) 
52. The foci of the ellipse 
and the hyperbola 
Then, the value of b2 is
(1) 1
(2) 5
(3) 7
(4) 9
53. A tetrahedron has vertices at O(0, 0, 0), A(1, 2, 1) B(2, 1, 3) and C(−1, 1, 2). Then, the angle between the faces OAB and ABC will be
(1) cos−1(19/35)
(2) cos−1(17/31)
(3) 30°
(4) 90°
54. The radius of the circle in which the sphere x2 + y2 + z2 + 2x – 2y – 4z – 19 = 0 is cut be the plane x + 2y + 2z + 7 = 0, is
(1) 1
(2) 2
(3) 3
(4) 4
55. The lines 
are coplanar, if
(1) k = 0 or −1
(2) k = 1 or −1
(3) k = 0 or −3
(4) k = 3 or −3
56. The two lines x = ay + b, z = cy + d and x = a’y + b’, z = c’y +d’ will be perpendicular, if and only if
(1) aa’ + bb’ + cc’ + 1 = 0
(2) aa’ + bb’ + cc’ = 0
(3) (a + a’)(b + b’) + (c + c’) = 0
(4) aa’ + cc’ + 1 = 0
57. The shortest distance from the plane 12x + 4y + 3z = 327 to the sphere x2 + y2 + z2 + 4x – 2y – 6z = 155 is
(1) 26
(2) 11 (4/13)
(3) 13
(4) 39
58. Two systems of rectangular axes have the same origin. If a plane cuts them at distances a, b, c and a’, b’, c’ from the origin, then
(1) 
(2) 
(3) 
(4) 
59. 
are three vectors, such that 
then 
is equal to
(1) 0
(2) −7
(3) 7
(4) 1
60. If 
are three non-coplanar vectors, then
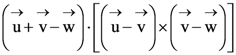equals
(1) 0
(2) 
(3) 
(4) 
61. Consider points A, B, C and D with position vectors 
and 
Then, ABCD is a
(1) square
(2) rhombus
(3) rectangle
(4) √17
62. The vectors 
are the sides of a ∆ABC. The length of the median through A is
(1) √18
(2) √72
(3) √33
(4) √288
63. A particle acted on by constant forces 
is displaced from the point 
to the point 
The total work done by the forces is
(1) 20 unit
(2) 30 unit
(3) 40 unit
(4) 50 unit
64. Let 
If 
is a unit vector such that 
then 
is equal to
(1) 0
(2) 1
(3) 2
(4) 3
65. The median of a set of 9 distinct observations is 20.5. If each of the largest 4 observations of the set is increased by 2, then the median of the new set
(1) is increased by 2
(2) is decreased by 2
(3) is two times the original median
(4) remains the same as that of the original set
66. In an experiment with 15 observations on x, the following results were available
∑ x2 = 2830, ∑ x = 170.
One observations that was 20, was found to be wrong and was replaced by the correct value 30. Then, the corrected variance is
(1) 78.00
(2) 188.66
(3) 177.33
(4) 8.33
67. Five horses are in a race. Mr. A selects two of the horses at random and bets on them. The probability that Mr. A selected the winning horse, is
(1) 4/5
(2) 3/5
(3) 1/5
(4) 2/5
68. Events, A, B, C are mutually exclusive events such that 
The set of possible values of x are in the interval
(1) [1/3, 1/2]
(2) [1/3, 2/3]
(3) [1/3, 13/3]
(4) [0, 1]
69. The mean and variance of a random variable X having a binomial distribution are 4 and 2 respectively, then P(X = 1) is
(1) 1/32
(2) 1/16
(3) 1/8
(4) 1/4
70. The resultant of forces 
is doubled, then 
is doubled. If the directions of 
is again doubled, then P2 : Q2 : R2 is
(1) 3 : 1 : 1
(2) 2 : 3 : 2
(3) 1 : 2 : 3
(4) 2 : 3 : 1
71. Let R1 and R2 respectively be the maximum ranges up and down an inclined plane and R be the maximum range on the horizontal plane. Then, R1, R, R2 are in
(1) AGP
(2) AP
(3) GP
(4) HP
72. A couple is of moment 
and the force forming the couple is 
. If is turned through a right angle, the moment of the couple thus formed is 
If instead, the forces is turned through an angle α, then the moment of couple becomes
(1) 
(2) 
(3) 
(4) 
73. Two particles start simultaneously from the same point and move along two straight lines, one with uniform velocity 
and the other from rest with uniform acceleration 
Let α be the angle between their directions of motion. The relative velocity of the second particle w.r.t. the first is least after a time
(1) 
(2) 
(3) u sin α
(4) 
74. Two stones are projected from the top of a cliff h meters high, with the same speed u, so as to hit the ground at the same spot. If one of the stones is projected horizontally and the other is projected at an angle θ to the horizontal, then tan θ equals
(1) 
(2) 
(3) 
(4) 
75. A body travels a distance s in t seconds. It starts from rest and ends at rest. In the first part of the journey, it moves with constant acceleration f and in the second part with constant retardation r. The value of t is given by
(1) 
(2) 
(3) 
(4) 
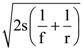
Latest Govt Job & Exam Updates: