JEE Main (AIEEE) 2004
Mathematics
1. Let R = {(1, 3), (4, 2), (2, 4), (2, 3), (3, 1)} be a relation on the set A = {1, 2, 3, 4}. The relation R is
(1) a function
(2) transitive
(3) not symmetric
(4) reflexive
2. The range of the function f(x) = 7 − xPx−3 is
(1) {1, 2, 3}
(2) {1, 2, 3, 4, 5, 6}
(3) {1, 2, 3, 4}
(4) {1, 2, 3, 4, 5}
3. Let z, w be complex numbers such that ![]() and arg (zw) = π. Then, arg (z) equals
and arg (zw) = π. Then, arg (z) equals
(1) π/4
(2) π/2
(3) 3π/4
(4) 5π/4
4. If z = x – iy and z1/3 = p + iq, then 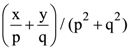 is equal to
is equal to
(1) 1
(2) −1
(3) 2
(4) −2
5. If |z2 – 1| = |z|2 + 1, then z lies on
(1) the real axis
(2) the imaginary axis
(3) a circle
(4) an ellipse
6. Let 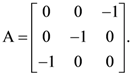 The only correct statement about the matrix A is
The only correct statement about the matrix A is
(1) A is a zero matrix
(2) A = (−1) I, where I is a unit matrix
(3) A−1 does not exist
(4) A2 = I
7. Let 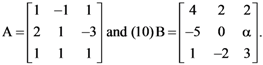 If B is the inverse of matrix A, then α is
If B is the inverse of matrix A, then α is
(1) −2
(2) 1
(3) 2
(4) 5
8. If a1, a2, a3,……., an, …… are in GP, then the value of the determinant 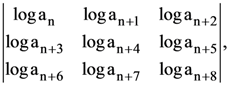 is
is
(1) 0
(2) 1
(3) 2
(4) −2
9. Let two numbers have arithmetic mean 9 and geometric mean 4. Then, these numbers are the roots of the quadratic equation
(1) x2 + 18x + 16 = 0
(2) x2 – 18x + 16 = 0
(3) x2 + 18x – 16 = 0
(4) x2 – 18x – 16 = 0
10. If (1 – p) is a root of quadratic equation x2 + px + (1 – p) = 0, then its roots are
(1) 0, 1
(2) −1, 1
(3) 0, −1
(4) −1, 2
11. Let S(K) = 1 + 3 + 5 + . . . +(2K – 1) = 3 + K2. Then, which of the following is true?
(1) S(1) is correct
(2) S(K) ⇒S(K +1)
(3) S(K) ⇏ S(K + 1)
(4) Principle of mathematical induction can be used to prove the formula
12. How many easy are there to arrange the letter in the word GARDEN with the vowels in alphabetical order ?
(1) 120
(2) 240
(3) 360
(4) 480
13. The number of ways of distributing 8 identical balls in 3 distinct boxes, so that none of the boxes is empty, is
(1) 5
(2) 21
(3) 38
(4) 8C3
14. If one root of the equation x2+ px + 12 = 0 is 4, while the equation x2 + px + q = 0 has equal roots, then the value of ‘q’ is
(1) 49/4
(2) 12
(3) 3
(4) 4
15. The coefficient of the middle term in the binomial expansion in powers of x of (1 + αx)4 and of (1 – αx)6 is the same, if α equals
(1) −5/3
(2) 10/3
(3) −3/10
(4) 3/5
16. The coefficient of xn in the expansion of (1 + x)(1 – x)n is
(1) (n – 1)
(2) (−1)n (1 – n)
(3) (−1)n−1 (n – 1)2
(4) (−1)n−1 n
17. If 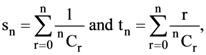 then tn/sn is equal to
then tn/sn is equal to
(1) n/2
(2) ![]()
(3) n – 1
(4) ![]()
18. Let Tr be the rth term of an AP whose first term is a and common difference is d. If for some positive integers m, n, m ≠ n, Tm = 1/n and Tn = 1/m, then a – d equals
(1) 0
(2) 1
(3) 1/mn
(4) ![]()
19. The sum of the first n terms of the series 12 + 2∙22 + 32 + 2∙42 + 52 + 2∙62 + . . . is ![]() when n is even. When n is odd the sum is
when n is even. When n is odd the sum is
(1) ![]()
(2) ![]()
(3) ![]()
(4) 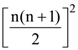
20. The sum of series ![]()
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
21. Let α, β be such that π < α – β < 3π. If ![]() then the value of
then the value of ![]()
(1) −3/√130
(2) 3/√130
(3) 6/65
(4) −6/65
22. If ![]() then the difference between the maximum and minimum values of u2 is given by
then the difference between the maximum and minimum values of u2 is given by
(1) 2(a2 + b2)
(2) ![]()
(3) (a + b)2
(4) (a – b)2
23. The sides of a triangle are sin α, cos α and ![]() for some 0 < α < π/2. Then, the greatest angle of the triangle is
for some 0 < α < π/2. Then, the greatest angle of the triangle is
(1) 60°
(2) 90°
(3) 120°
(4) 150°
24. A person standing on the bank of a river, observes that the angle of elevation of the top of a tree on the opposite bank of the river is 60° and when he retires 40 m away from the tree the angle of elevation becomes 30°. The breadth of the river is
(1) 20 m
(2) 30 m
(3) 40 m
(4) 60 m
25. If f : R → S, defined by f(x) = sin x −√3 cos x + 1, is onto, then the interval of S is
(1) [0, 3]
(2) [−1, 1]
(3) [0, 1]
(4) [−1, 3]
26. The graph of the function y = f(x) is symmetrical about the line x = 2, then
(1) f(x + 2) = f(x – 2)
(2) f(2 + x) = f(2 – x)
(3) f(x) = f(−x)
(4) f(x) = −f(−x)
27. The domain of the function 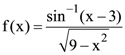 is
is
(1) [2, 3]
(2) [2, 3)
(3) [1, 2]
(4) [1, 2)
28. If 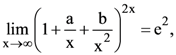 then the values of a and b are
then the values of a and b are
(1) a ∈ R, b ∈ R
(2) a = 1, b ∈ R
(3) a ∈ R, b = 2
(4) a = 1, b = 2
29. Let ![]() x ≠ π /4, x ∈[0, π/2]. If f(x) is continuous in [0, π/2], then f(π/4) is
x ≠ π /4, x ∈[0, π/2]. If f(x) is continuous in [0, π/2], then f(π/4) is
(1) 1
(2) 1/2
(3) −1/2
(4) −1
30. If ![]() , x> 0, then (dy/dx) is
, x> 0, then (dy/dx) is
(1) ![]()
(2) 1/x
(3) ![]()
(4) ![]()
31. A point on the parabola y2 = 18x at which the ordinate increases at twice the rate of the abscissa, is
(1) (2, 4)
(2) (2, −4)
(3) (−9/8, 9/2)
(4) (9/8,9/2)
32. A function y = f(x) has a second order derivative f”=6(x – 1). If its graph passes through the point (2, 1) and at that point the tangent to the graph is y = 3x – 5, then the function is
(1) (x – 1)2
(2) (x – 1)3
(3) (x + 1)3
(4) (x + 1)2
33. The normal to the curve x =a(1 + cos θ), y = a sin θ at ‘θ’ always passes through the fixed point
(1) (a, 0)
(2) (0, a)
(3) (0, 0)
(4) (a, a)
34. If 2a + 3b + 6c = 0, then at least one root of the equation ax2 + bx + c = 0 lies in the interval
(1) (0, 1)
(2) (1, 2)
(3) (2, 3)
(4) (1, 3)
35. 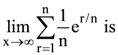
(1) e
(2) e – 1
(3) 1 – e
(4) e + 1
36. If ![]() then value of (A, B) is
then value of (A, B) is
(1) (sin α, cos α)
(2) (cos α, sin α)
(3) (−sin α, cos α)
(4) (−cos α, sin α)
37. ![]()
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
38. The value of ![]() is
is
(1) 28/3
(2) 14/3
(3) 7/3
(4) 1/3
39. The value of 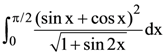 is
is
(1) 0
(2) 1
(3) 2
(4) 3
40. If ![]() then A is equal to
then A is equal to
(1) 0
(2) π
(3) π/4
(4) 2π
41. If 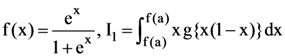 and
and ![]() then the value of I2/I1 is
then the value of I2/I1 is
(1) 2
(2) −3
(3) −1
(4) 1
42. The area of the region bounded by the curves y = |x – 2|, x = 1, x = 3 and the x-axis is
(1) 1
(2) 2
(3) 3
(4) 4
43. The differential equation for the family curves x2 + y2 − 2ay = 0, where a is an arbitrary constant, is
(1) 2(x2 – y2)y’ = xy
(2) 2(x2 + y2) y’ = xy
(3) (x2 – y2) y’ = 2xy
(4) (x2 + y2) y’ = 2xy
44. The solution of the differential equation y dx + (x + x2y) dy = 0 is
(1) ![]()
(2) ![]()
(3) ![]()
(4) log y = cx
45. Let A(2, −3) and B(−2, 1) be vertices of a ∆ABC. If the centroid of this triangle moves on the line 2x + 3y = 1, then the locus of the vertex C is the line
(1) 2x + 3y = 9
(2) 2x – 3y = 7
(3) 3x + 2y = 5
(4) 3x – 2y = 3
46. The equation of the straight line passing through the point (4, 3) and making intercepts on the coordinate axes whose sum is −1, is
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
47. If the sum of the slopes of the lines given by x2 – 2cxy – 7y2 = 0 is four times their product, then c has the value
(1) 1
(2) −1
(3) 2
(4) −2
48. If one of the lines given by 6x2 – xy + 4cy2 = 0 is 3x + 4y = 0, then c equals
(1) 1
(2) −1
(3) 3
(4) −3
49. If a circle passes through the point (a, b) and cuts the circle x2 + y2 = 4 orthogonally, then the locus of its centre is
(1) 2ax + 2by + (a2 + b2 + 4) = 0
(2) 2ax + 2by – (a2 + b2 + 4) = 0
(3) 2ax – 2by + (a2 + b2 + 4) = 0
(4) 2ax – 2by − (a2 + b2 + 4) = 0
50. A variable circle passes through the fixed pint A(p, q) and touches x-axis. The locus of the other end of the diameter through A is
(1) (x – p)2 = 4qy
(2) (x – q)2 = 4py
(3) (y – p )2 = 4qx
(4) (y – q)2 = 4px
51. If the lines 2x + 3y + 1 = 0 and 3x – y – 4 = 0 lie along diameters of a circle of circumference 10 π, then the equation of the circle is
(1) x2 + y2 – 2x + 2y – 23 = 0
(2) x2 + y2 – 2x − 2y – 23 = 0
(3) x2 + y2 + 2x + 2y – 23 = 0
(4) x2 + y2 + 2x − 2y – 23 = 0
52. The intercept on the line y = x by the circle x2 + y2 – 2x = 0 is AB. Equation of the circle on AB as a diameter is
(1) x2 + y2 – x – y = 0
(2) x2 + y2 – x + y = 0
(3) x2 + y2 + x + y = 0
(4) x2 + y2 + x – y = 0
53. If a ≠ 0 and the line 2bx + 3cy + 4d = 0 passes through the points of intersection of the parabolas y2 = 4ax and x2 = 4ay, then
(1) d2 + (2b + 3c)2 = 0
(2) d2 + (3b + 2c)2 = 0
(3) d2 + (2b – 3c)2 = 0
(4) d2 + (3b – 2c)2 = 0
54. The eccentricity of an ellipse with its centre at the origin, is ½. If one of the directrices is x = 4, then the equation of the ellipse is
(1) 3x2 + 4y2 = 1
(2) 3x2 + 4y2 = 12
(3) 4x2 + 3y2 = 12
(4) 4x2 + 3y2 = 1
55. A line makes the same angle θ with each of the x and z axes. If the angle β, which it makes with y-axis, is such that sin2 β = 3 sin2 θ, then cos2 θ equals
(1) 2/3
(2) 1/5
(3) 3/5
(4) 2/5
56. Distance between two parallel planes 2x + y + 2z = 8 and 4x + 2y + 4z + 5 = 0 is
(1) 3/2
(2) 5/2
(3) 7/2
(4) 9/2
57. A line with direction cosines proportional to 2, 1, 2 meets each of the lines x = y + a = z and x + a = 2y = 2z. The coordinates of each of the points of intersection are given by
(1) (3a, 3a, 3a), (a, a, a)
(2) (3a, 2a, 3a), (a, a, a)
(3) (3a, 2a, 3a), (a, a, 2a)
(4) (2a, 3a, 3a), (2a, a, a)
58. If he straight lines x = 1 + s, y = −3 – λ s, z = 1 + λs and x = t/2, y = 1 +t, z = 2 – t , with parameters s and t respectively, are coplanar, then λ equals
(1) −2
(2) −1
(3) −1/2
(4) 0
59. The intersection of the spheres x2 + y2 + z2 + 7x – 2y – z = 13 and x2 + y2 + z2 – 3x + 3y + 4z = 8 is the same as the intersection of one of the sphere and the plane
(1) x – y – z = 1
(2) x – 2y – z = 1
(3) z – y – 2z = 1
(4) 2x – y – z = 1
60. Let ![]() be three non-zero vectors such that no two of these are collinear. If the vector
be three non-zero vectors such that no two of these are collinear. If the vector ![]() is collinear with
is collinear with ![]() collinear with
collinear with ![]() (λ being some non-zero scalar), then
(λ being some non-zero scalar), then ![]() equals
equals
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
61. A particle is acted upon by constant forces ![]() which displace it from a point
which displace it from a point ![]() to the point
to the point ![]() The work done in standard units by the forces is given by
The work done in standard units by the forces is given by
(1) 40
(2) 30
(3) 25
(4) 15
62. If ![]() are non-coplanar vectors and λ is a real number, then the vectors
are non-coplanar vectors and λ is a real number, then the vectors ![]() are non-coplanar for
are non-coplanar for
(1) all values of λ
(2) all except one value of λ
(3) all except two values of λ
(4) no value of λ
63. Let ![]() be such that
be such that 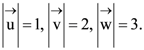 If the projection
If the projection ![]() is equal to that of
is equal to that of ![]() are perpendicular to each other, then
are perpendicular to each other, then 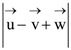 equals
equals
(1) 2
(2) √7
(3) √14
(4) 14
64. Let ![]() be non-zero vectors such that
be non-zero vectors such that 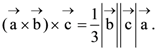 If θ is the acute angle between the vectors
If θ is the acute angle between the vectors ![]() then sin θ equals
then sin θ equals
(1) 1/3
(2) √2/3
(3) 2/3
(4) 2√2/3
65. Consider the following statements
(1) Mode can be computed from histogram
(2) Median is not independent of change of scale.
(3) Variance is independent of change of origin and scale.
Which of these is/are correct?
(1) Only (1)
(2) Only (2)
(3) Only (1) and (2)
(4) (1), (2) and (3)
66. In a series of 2n observations, half of them equal a and remaining half equal –a. If the standard deviation of the observations is 2, then |a| equals
(1) 1/n
(2) √2
(3) 2
(4) √2/n
67. The probability that A speaks truth is 4/5 while this probability for B is 3/4. The probability that they contradict each other when asked to speak on a fact, is
(1) 3/20
(2) 1/5
(3) 7/20
(4) 4/5
68. The mean and the variance of a binomial distribution are 4 and 2 respectively. Then, the probability of 2 successes is
(1) 37/256
(2) 219/256
(3) 128/256
(4) 28/256
69. With two forces acting at a point, the maximum effect is obtained when their resultant is 4N. If they act at right angles, then their resultant is 3N. Then the forces are
(1) (2 + √2) N and ( 2 −√2) N
(2) (2 + √3) N and ( 2 – √3)N
(3) (2 + (1/2) √2)N and (2 (– 1/2) √2)N
(4) (2 + (1/2)√3)N and (2 (– 1/2) √3)N
70. In a right angle ∆ABC, ∠A = 90° and sides a, b, c are respectively, 5 cm, 4 cm and 3 cm. If a force ![]() has moments 0, 9 and 16 in N cm unit respectively about vertices A, B and C, the magnitude of
has moments 0, 9 and 16 in N cm unit respectively about vertices A, B and C, the magnitude of ![]() is
is
(1) 3
(2) 4
(3) 5
(4) 9
71. Three forces ![]() acting along IA, IB and IC, where I is the incentre of a ∆ABC, are in equilibrium. Then
acting along IA, IB and IC, where I is the incentre of a ∆ABC, are in equilibrium. Then ![]() is
is
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
72. A particle moves towards east from a point A to a point B at the rate of 4 km/h and then towards north from B to C at rate of 5 km/h. If AB = 12 km and BC = 5 km, then its average speed for its journey from A to C and resultant average velocity direct from A to C are respectively
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
73. A velocity (1/4) m/s is resolved into two components along OA and OB making angles 30° and 45° respectively with the given velocity. Then, the component along OB is
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
74. If t1 and t2 are the times of the flight of two particles having the same initial velocity u and range R on the horizontal, then is equal ![]() to
to
(1) u2 /g
(2) 4u2 /g2
(3) u2 /2g
(4) 1
75. A random variable X has the probability distribution

For the events E = {X is a prime number} and F = {X < 4}, the probability P(E ∪ F) is
(1) 0.87
(2) 0.77
(3) 0.35
(4) 0.50
Latest Govt Job & Exam Updates: