Physics
1. An electron gun is placed inside a long solenoid of radius R on its axis. The solenoid has 
and carries a current i. The electron gun shoots an electron along the radius of solenoid with speed If the electron does not hit the surface of the solenoid, maximum possible value of v is (all symbols have their standard meaning):
(a) 
(b) 
(c) 
(d) 
2. Two identical capacitors A and B, charged to the same potential 5V are connected in two different circuit as shows below at time t=0. If the charges on capacitors A and B at time t= CR is QA and QB respectively, then (Here is the base of natural logarithm)
(a) CV, CV/e
(b) CV/e, CV/2e
(c) CV/e, VC/2
(d) CV/e, CV
3. For the four sets of three measured physical quantities as given below. Which of the following options is correct?
(i) A1 = 24.36, B1=0.0724, C1= 256.2
(ii) A2 = 24.44, B2=16.08, C2= 240.2
(iii) A3 = 25.2, B3 = 19.2812, C3= 236.183
(iv) A4 = 25, B4 = 236.191, C4 = 19.5
(a) A4 + B4 + C4 < A1 + B1 + C1 < A2 + B2 + C2 = A3 + B3 +C3
(b) A1 + B1 + C1 = A2 + B2 + C2 = A3 + B3 + C3 = A4 + B4 + C4
(c) A1 + B1 + C1 < A3 + B3 +C3 < A2 + B2 + C2 < A4 + B4 +C4
(d) A4 + B4 +C4 < A1 + B1 +C1< A3 + B3 +C3 < A2 + B2 +C2
4. A particle starts from the origin at t = 0 with an initial velocity of 
from origin and moves in the x-y plane with a constant acceleration 
The x-coordinate of the particle at the instant when its y-coordinated is 32 m is D meters. The value of D is:
(a) 60
(b) 50
(c) 32
(d) 40
5. A spring mass system (mass m, spring constant k and natural length l) rest in equilibrium on a horizontal disc. The free end of the spring is fixed at the center of the disc. If the disc together with spring mass system, rotates about its axis with an angular velocity (k >>> mω2), the relative change in the length of the spring is best given by the option:
(a) 
(b) 
(c) 
(d) 
6. A small circular loop of conducting wire has radius a and carries current i. It is placed in a uniform magnetic field B perpendicular to its plane such that when rotated slightly about its diameter and released, its starts performing simple harmonic motion of time period T. If the mass of the loop is m then
(a)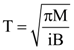 
(b)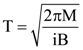 
(c)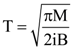 
(d)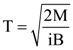 
7. A small spherical droplet of density d is floating exactly half immersed in a liquid of density ρ and surface tension T. The radius of droplet is (take note that the surface tension applied an upward force on droplet)
(a)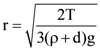 
(b)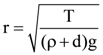 
(c) 
(d)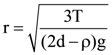 
8. A wire of length L and mass 6 x 10−3 kg/m per unit length is put under tension of 540N. Two consecutive frequencies that it resonates at are: 420 Hz and 490 Hz . Then L in meter is
(a) 8.1 m
(b) 2.1 m
(c) 1.1 m
(d) 5.1 m
9. A plane electromagnetic wave is propagating along the direction 
with the polarization along the direction 
The correct form of the magnetic field of the wave would be (here B0 is an appropriate constant)
(a)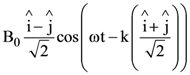 
(b)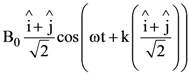 
(c)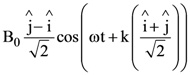 
(d)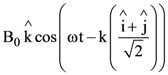 
10. Two gases-Argon (atomic radius 0.07 nm atomic weight 40) and Xenon (atomic radius 0.1 nm atomic weight 140) have the same number density and are at the same temperature. The ratio of their respective mean free time is closest to
(a) 4.67
(b) 2.04
(c) 1.83
(d) 3.67
11. Two steel wires having same length are suspended from a ceiling under the same load. If the ratio of their energy stored per unit volume is 1: 4, the ratio of their diameters is:
(a) √2:1
(b) 1:√2
(c) 1:2
(d) 2:1
12. Planets A has a mass M and radius R. Planet B has the mass and half the radius of planet A. If the escape velocities from the planets A and B are vA and vB respectively, then surfaces is 
the value of n is:
(a) 3
(b) 2
(c) 4
(d) 5
13. A rod of length L has non-uniform linear mass density given by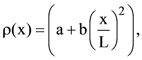 
where a and b are constants and 0 ≤ x ≤ The value of x for the center of mass of the rod is at:
(a) 
(b) 
(c) 
(d) 
14. A particle of mass m is projected with a speed u from the ground at angle is θ = π/3 w.r.t. horizontal (x-axis). When it has reached its maximum height, it collides completely inelastically with another particle of the same mass and velocity 
The horizontal distance covered by the combined mass before reaching the ground is:
(a)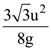 
(b)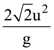 
(c) 
(d)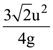 
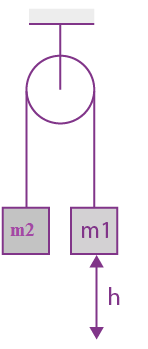
15. A uniformly thick wheel with moment of inertia I and radius R is free to rotate about its center of mass (see fig). A massless string is wrapped over its rim and two blocks of massless string is wrapped over its rim and two blocks of masses m1 and m2 (m1 > m2 ) are attached to the ends of string. The system is released from rest. The angular speed of the wheel when m1 descend by a distance h is:
(a) 
(b)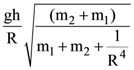 
(c) 
(d) 
16. The energy required to ionise a hydrogen like ion in its ground state is 9 Rydbergs. What is the wavelength of the radiation emitted when the electron in this ion jumps from the second excited state to the ground stare?
(a) 8.6
(b) 11.4
(c) 24.2
(d) 35.8
17. There is a small source of light at some depth below the surface of water (refractive index 4/3) in a tank of large cross sectional surface area. Neglecting any reflection from the bottom and absorption by water, percentage of light that emerges out of surface is (nearly): [Use the fact that surface area of a spherical cap of height h and radius of curvature r is 2πrh]
(a) 17%
(b) 34%
(c) 50%
(d) 21%
18. An electron of mass m and magnitude of charge |e| initially at rest gets accelerated by a constant electric field E. The of charge of de-Broglie wavelength of this electron at time t ignoring relativistic effects is
(a) 
(b) 
(c) 
(d) 
19. In LC circuit the inductance L = 40mH and C = 100 μF. If a voltage V(t) = 10sin(314t) is applied to the circuit, the current in the circuit is given as
(a) 10cos (314t)
(b) 0.52cos (314t)
(c) 0.52sin (314t)
(d) 5.2cos (314t)
20. The current (i) in the network is
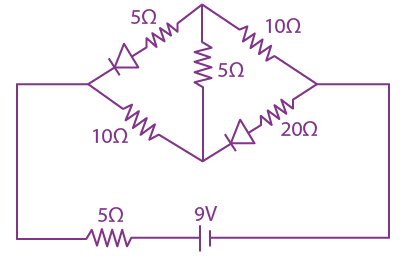
(a) 0 A
(b) 0.3 A
(c) 0.2 A
(d) 0.6 A
21. Starting at temperature 300 K, one mole of an ideal diatomic gas (γ = 1.4) is first compressed adiabatically from volume to V1 to V2 = V1/16. It is then allowed to expand isobarically to volume 2V2 . If all the processes are the quasi-static then the final temperature of the gas (0K) is (to the nearest integer)
22. An electric field 
passes through the box shown in figure. The flux of the electric field through surface ABCD and BCGF are marked as ϕ1 and ϕ2, then difference between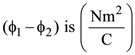 
23. In a Young’s double slit experiment 15 fringes are observed on a small portion of the screen when light of wavelength 500nm is used. 10 fringes are observed on the same section of the screen when another light source of wavelength λ is used. Then the value of λ is (nm)
24. In a meter bridge experiment S is a standard resistance. R is a resistance wire. It is found that balancing length is l = 25 cm. If R is replaced by a wire of half length and half diameter that of R of same material, then the balancing l (in cm) will now be
25. The circuit shown below is working as a 8V dc regulated voltage source. When 12V is used as input, the power dissipated (in mW) in each diode id; (considering both zener diode are identical).
Chemistry
1. 5 g of Zinc is treated separately with an excess of
(I) dilute hydrochloric acid and
(II) aqueous sodium hydroxide.
The ratio of the volumes of H2 evolved in these two reactions is:
(a) 2 : 1
(b) 1 : 2
(c) 1 : 1
(d) 1 : 4
2. The solubility product of Cr(OH)3 at 298 K is 6×10−31 . The concentration of hydroxide ions in a saturated solution Cr(OH)3 will be:
(a) (18×10−31)1/4
(b) (18×10−31)1/2
(c) (2.22×10−31)1/4
(d) (4.86×10−31)1/4
3. Among the statements (a)-(d), the correct ones are:
(a) Lithium has the highest hydration enthalpy among the alkali metals.
(b) Lithium chloride is insoluble in pyridine.
(c) Lithium cannot form ethynide upon its reaction with ethyne.
(d) Both lithium and magnesium react slowly with H2O.
(a) (a), (b) and (d) only
(b) (b) and (c) only
(c) (a), (c) and (d) only
(d) (a) and (d) only
4. The first and second ionization enthalpies of a metal are 496 and 4560 kJ mol−1 How many moles of HCl and H2SO4, respectively, will be needed to react completely with 1 mole of metal hydroxide?
(a) 1 and 2
(b) 1 and 0.5
(c) 1 and 1
(d) 2 and 0.5
5. In the figure shown below reactant A (represented by the square) is in equilibrium with product B (represented by circle). The equilibrium constant is:
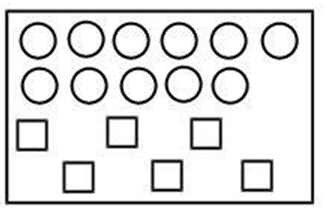
(a) 1
(b) 2
(c) 8
(d) 4
6. The correct order spin-only magnetic moments of the following complexes is:
I. [Cr(H2O)6]Br2
II. Na4[FeCN6]
III. Na3[Fe(C2O4)3] (∆0 > P)
IV. (Et4N)2[CoCl4]
(a) (III)>(I)>(II)>(IV)
(b) (III)>(I)>(IV)>(II)
(c) (I)>(IV)>(III)>(II)
(d) (II)≈(I)>(IV)>(III)
7. The true statement amongst the following.
(a) S is a function of temperature but S is not a function of temperature.
(b) Both S and S are functions of temperature.
(c) Both S and S are not functions of temperature.
(d) S is not a function of temperature but S is a function of temperature.
8. The reaction of H3N3B3Cl3 (A) with LiBH4 in tetrahydrofuran gives inorganic benzene (B). Furthur, the reaction of (A) with (C) leads to H3N3B3(Me)3. Compounds (B) and (C) respectively, are:
(a) Boron nitride, MeBr
(b) Diborane, MeMgBr
(c) Borazine, MeBr
(d) Borazine, MeMgBr
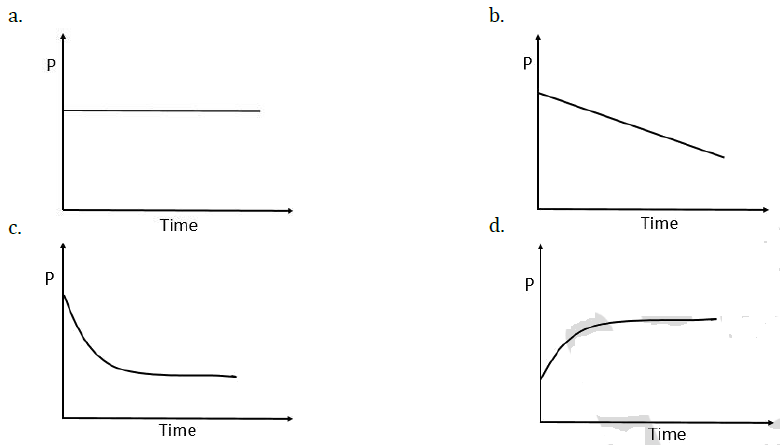
9. A mixture of gases O2, H2 and CO are taken in a closed vessel containing charcoal. The graph that represents the correct behaviour of pressure with time is:
10. The isomer(s) of [Co(NH3)4Cl2] that has/have a Cl-Co-Cl angle of 90°, is/are:
(a) cis only
(b) trans only
(c) meridional and trans
(d) cis and trans
11. Amongst the following, the form of water with lowest ionic conductance at 298 K is:
(a) distilled water
(b) sea water
(c) saline water used for intra venous injection
(d) water from a well
12. The number of sp2 hybrid orbitals in molecule of benzene is:
(a) 18
(b) 24
(c) 6
(d) 12
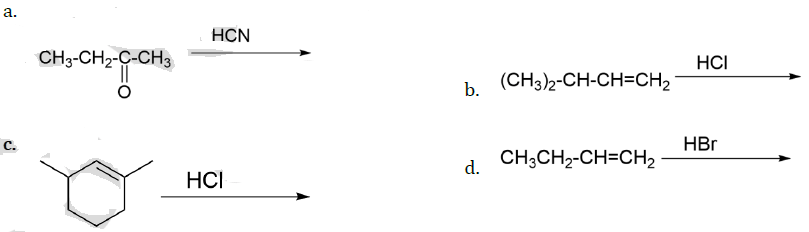
13. Which of the following reactions will not produce a racemic product?
14. Which of the following has the shortest C-Cl bond?
(a) Cl―CH=CH2
(b) Cl―CH=CH―CH3
(c) Cl―CH=CH―OCH3
(d) Cl―CH=CH―NO2
15. Biochemical oxygen demand (BOD) is the amount of oxygen required (in ppm):
(a) for the photochemical breakdown of waste present in 1m3 volume of a water body.
(b) by anaerobic bacteria to break-down inorganic waste present in a water body.
(c) by bacteria to break-down organic waste in a certain volume of water sample.
(d) for sustaining life in a water body.
16. Which polymer has chiral, monomer(s)?
(a) Buna-N
(b) Neoprene
(c) Nylon 6,6
(d) PHBV
17. A, B and C are three biomolecules. The results of the tests performed on them are given below:
| Molisch’s Test | Barfoed Test | Biuret Test | |
| A | Positive | Negative | Negative |
| B | Positive | Positive | Negative |
| C | Negative | Negative | Positive |
A, B and C are respectively
(a) A = Lactose B = Glucose C = Albumin
(b) A = Lactose B = Glucose C = Alanine
(c) A = Lactose B = Fructose C = Alanine
(d) A = Glucose B = Sucrose C = Albumin
18. The decreasing order of basicity of the following amines is:
(a) I > II > III > IV
(b) IV > III > I > II
(c) II > I > III > IV
(d) IV > I > II > III
19. 
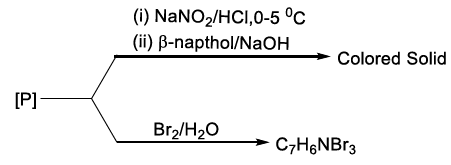
The compound [P] is
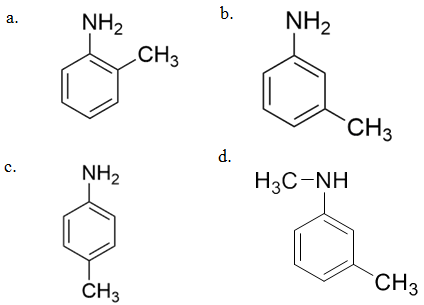
20. In the following reaction A is :
21. The sum of total number of bonds between chromium and oxygen atoms in chromate and dichromate ions is:
22. A sample of milk splits after 60 min. at 300K and after 40 min at 400K when the population of lactobacillus acidophilus in it doubles . The activation energy (in kJ/mol) for this process is closest to : (Given, R = 8.3 J mol−1K−1), ln(2/3) = 0.4, e−3 = 4.0)
23. One litre of sea water (d =1.03g/cm3) contains 10.3 mg of O2 Determine the concentration of O2 in ppm:
24. A cylinder containing an ideal gas (0.1 mol of 1.0 dm3 ) is in thermal equilibrium with a large volume of 0.5 molal aqueous solution of ethylene glycol at it freezing point. If the stoppers S1 and S2 (as shown in the figure) suddenly withdrawn, the volume of the gas in liters after equilibrium is achieved will be: (Given, Kf (water) = 2.0 K kg mol−1 ,R = 0.08 dm3 atm K−1 mol−1)
25. Consider the following reactions;
The mass percentage of carbon in A is:
Mathematics
1. If A = {x∈ R∶ |x| <2} and B = {x∈ R∶ |x−2| ≥3} then :
(a) A − B = [−1,2]
(b) B − A = R− (−2, 5)
(c) A ⋃ B = R− (2,5)
(d) A ∩ B = (−2, −1)
2. If 10 different balls has to be placed in 4 distinct boxes at random, then the probability that two of these boxes contain exactly 2 and 3 balls is :
(a) 965/210
(b) 945/210
(c) 945/211
(d) 965/211
3. If x = 2 sin θ − sin 2 θ and y = 2 cos θ − cos 2 θ, θ ∈ [0, 2π], then d2y/dx2 at θ =π is:
(a) −3/8
(b) 3/4
(c) 3/2
(d) −3/4
4. Let f and g be differentiable functions on R, such that fog is the identity function. If for some a, b ∈ R, g’(a) = 5 and g(a) = b, then f'(b) is equal to :
(a) 2/5
(b) 5
(c) 1
(d) 1/5
5. In the expansion of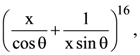 
if l1 is the least value of the term independent of x when 
and l2 is the least value of the term independent of x when 
then the ratio l2 : l1 is equal to:
(a) 16 : 1
(b) 8 : 1
(c) 1 : 8
(d) 1 : 16
6. Let a,b ∈R, a ≠ 0, such that the equation, ax2-2bx + 5 = 0 has a repeated root α, which is also a root of the equation x2 − 2bx − 10 = 0. If β is the root of this equation, then α2 + β2 is equal to:
(a) 24
(b) 25
(c) 26
(d) 28
7. Let a function f: [0, 5] → R, be continuous, f(1) = 3 and F be defined as:
Then for the function F, the point x = 1 is
(a) a point of inflection.
(b) a point of local maxima
(c) a point of local minima
(d) not a critical point
8. Let [t] denotes the greatest integer ≤ t and 
Then the function, f(x) = [x2] sin πx discontinuous, when x is equal to
(a) 
(b) √A
(c) 
(d) 
9. Let a – 2b + c = 1
If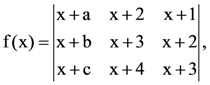 
then:
(a) f(−50) = 501
(b) f(−50) = −1
(c) f(50) = 1
(d) f(50) = −501
10. Given: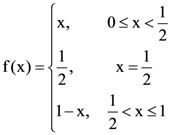 
and 
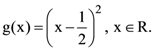Then the area (in sq. units) of the region bounded by the curves y = f(x) and y = g(x) between the lines 2x = 1 to 2x = √3 is:
(a) 
(b) 
(c) 
(d) 
11. The following system of linear equations
7x + 6y – 2z = 0
3x + 4y + 2z = 0
x – 2y – 6z = 0, has
(a) infinitely many solutions, (x, y, z) satisfying y = 2z
(b) infinitely many solutions (x, y, z) satisfying x = 2z
(c) no solution
(d) only the trivial solution
12. If p − > (p ∧~ q) is false. Then the truth values of p and q are respectively
(a) F, T
(b) T, F
(c) F, F
(d) T, T
13. The length of minor axis (along y-axis) of an ellipse of the standard form is 4/√3. If this ellipse touches the line x + 6y = 8, then its eccentricity is:
(a) 
(b)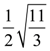 
(c) 
(d)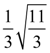 
14. If z be a complex number satisfying |Re(z)| + |Im(z)| = 4, then |𝑧| cannot be:
(a) √7
(b) 
(c) √10
(d) √8
15. If 
and 
where 0 < θ < π/4, then:
(a) y(1 + x) = 1
(b) x(1 – y) = 1
(c) y(1 – x) = 1
(d) x(1 + y) = 1
16. If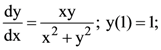 
then a value of x satisfying y(x) = e is:
(a) √3e
(b) 
(c) √2e
(d) e/√2
17. If one end of focal chord AB of the parabola y2 = 8x is at A(1/2, −2), then the equation of tangent to it at B is
(a) x + 2y + 8 = 0
(b) 2x – y – 24 = 0
(c) x – 2y + 8 = 0
(d) 2x + y – 24 = 0
18. Let an be the nth term of a G.P. of positive terms. If 
then 
is equal to:
(a) 300
(b) 175
(c) 225
(d) 150
19. A random variable X has the following probability distribution:
| X | 1 | 2 | 3 | 4 | 5 |
| P(X) | K2 | 2K | K | 2K | 5K2 |
Then P(X > 2) is equal to:
(a) 7/12
(b) 23/36
(c) 1/36
(d) 1/6
20. If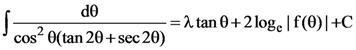 
where C is constant if integration, then the ordered pair (λ, f(θ)) is equal to:
(a) (−1, 1 – tan θ)
(b) (−1, 1 + tan θ)
(c) (1, 1 + tan θ)
(d) (1, 1 – tan θ)
21. Let 
be three vectors such that 
and the angle between 
is π/3. If 
is perpendicular to vector 
is equal to______
22. If Cr = 25Cr and C0 + 5 ∙ C1 + 9 ∙ C2 + … + 101 ∙ C25 = 225 ∙ k is equal to ________.
23. If the curves x2 − 6x + y2 +8 = 0 and x2 − 8y + y2 + 16 − k = 0, (k > 0) touch each other at a point, then the largest value of k is
24. The number of terms common to the A.P.’s 3,7,11,…407 and 2,9,16,…709 is __________.
25. If the distance between the plane. 23x – 10y – 2z + 48 = 0 and the plane containing the lines 
and 
(λ ∈ R) is equal to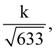 
then k is equal to ________.
Latest Govt Job & Exam Updates: