Physics
1. The mass density of a spherical galaxy K varies as K/r over a large distance ‘r’ from its centre. In that region, a small star is in a circular orbit of radius R. Then the period of revolution, T depends on R as:
(a) T2 ∝ R
(b) T2 ∝ R3
(c) T2 ∝ (1/R3)
(d) T ∝ R
2. An amplitude modulated wave is represented by the expression vm= 5(1 + 0.6 cos 6280 t )sin (211 × 104t) volts. The minimum and maximum amplitudes of the amplitude modulated wave are, respectively :
(a) 
(b) 5V, 8V
(c) 3V, 5V
(d) 
3. A spherical mirror is obtained as shown in the figure from a hollow glass sphere. If an object is positioned in front of the mirror, what will be the nature and magnification of the image of the object ? (Figure drawn as schematic and not to scale)
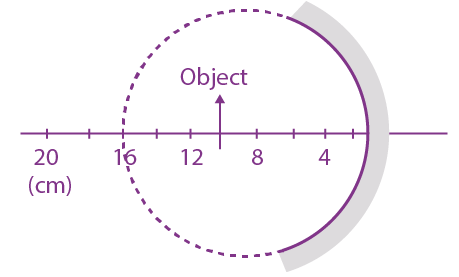
(a) Erect, virtual and unmagnified
(b) Inverted, real and magnified
(c) Erect, virtual and magnified
(d) Inverted, real and unmagnified
4. A cylindrical vessel containing a liquid is rotated about its axis so that the liquid rises at its sides as shown in the figure. The radius of vessel is 5 cm an and the angular speed of rotation is ω rad s−1. The difference in the height, h (in cm) of liquid at the centre of vessel and at the side will be:
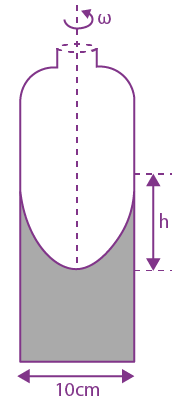
(a) 5ω2/2g
(b) 2ω2/25g
(c) 25ω2/2g
(d) 2ω2/5g
5. If speed V, area A and force F are chosen as fundamental units, then the dimension of;
Young’s modulus will be
(a) FA2V−3
(b) FA2V−2
(c) FA−1V0
(d) FA2V−1
6. A bead of mass m stays at point P (a, b) on a wire bent in the shape of a parabola y = 4Cx2 and rotating with angular speed ω (see figure). The value of ω is (neglect friction):
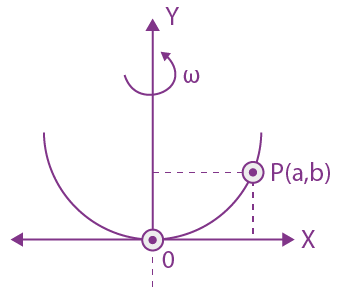
(a) 
(b) 2√gC
(c)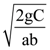 
(d) 2√2gC
7. Magnetic materials used for making permanent magnets (P) and magnets in a transformer (T) have different properties of the following, which property best matches for the type of magnet required?
(a) P : Small retentivity, large coercivity
(b) P : Large retentivity, large coercivity
(c) T : Large retentivity, large coercivity
(d) T : Large retentivity, small coercivity
8. Interference fringes are observed on a screen by illuminating two thin slits 1 mm apart with a light source (λ = 632.8 nm). The distance between the screen and the slits is 100cm. If a bright fringe is observed on screen at a distance of 1.27 mm from the central bright fringe, then the path difference between the waves, which are reaching this point from the slits is close to:
(a) 2.05 μm
(b) 2.87 nm
(c) 2 nm
(d) 1.27 μm
9. A gas mixture consists of 3 moles of oxygen and 5 moles of argon at temperature T. Assuming the gases to be ideal and the oxygen bond to be rigid, the total internal energy (in units of RT) of the mixture is:
(a) 11
(b) 13
(c) 15
(d) 20
10. A plane electromagnetic wave, has frequency of 2.0 × 1010 Hz and its energy density is 1.02 × 10–8 J/m3 in vacuum. The amplitude of the magnetic field of the wave is close
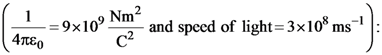
(a) 160 nT
(b) 150 nT
(c) 180 nT
(d) 190 nT
11. Consider four conducting materials copper, tungsten, mercury and aluminium with resistivity ρc, ρm, ρT and ρA Then:
(a) ρc > ρA > ρT
(b) ρA> ρm > ρc
(c) ρA> ρT > ρc
(d) ρm > ρA> ρc
12. A beam of protons with speed 4 × 105 ms–1 enters a uniform magnetic field of 0.3 T at an angle of 60° to the magnetic field. The pitch of the resulting helical path of protons is close to: (Mass of the proton =1.67 × 10–27 kg, charge of the proton =1.69 × 10–19C)
(a) 4 cm
(b) 2 cm
(c) 12 cm
(d) 5 cm
13. Two identical strings X and Z made of same material have tension Tx and Tz in them. If their fundamental frequencies are 450 Hz and 300 Hz, respectively, then the ratio Tx/Tz is:
(a) 2.25
(b) 1.25
(c) 0.44
(d) 1.5
14. A uniform cylinder of mass M and radius R is to be pulled over a step of height a(a < R) by applying a force F at its centre ‘O’ perpendicular to the plane through the axes of the cylinder on the edge of the step (see figure). The minimum value of F required is
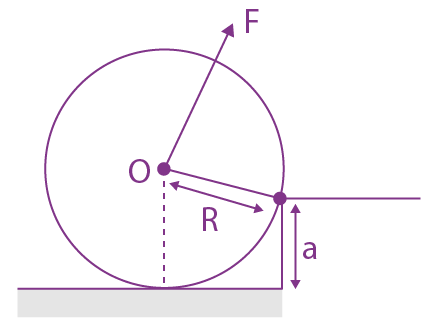
(a)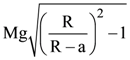 
(b)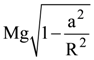 
(c) 
(d)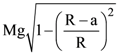 
15. In a reactor, 2 kg of 92U235 fuel is fully used up in 30 days. The energy released perfission is 200 MeV. Given that the Avogadro number, N = 6.023 × 1026 per kilo mole and1 eV =1.6 × 10–19 The power output of the reactor is close to
(a) 60 MW
(b) 54 MW
(c) 125 MW
(d) 35 MW
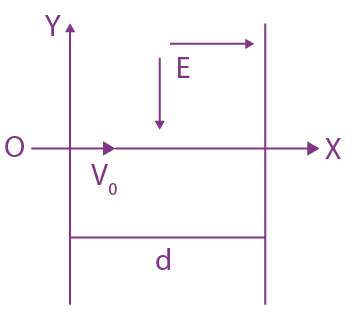
16. A charged particle (mass m and charge q) moves along X axis with velocity V0. When it passes through the origin it enters a region having uniform electric field 
which extends upto x = d. Equation of path of electron in the region x > d is:
(a)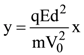 
(b)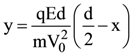 
(c)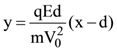 
(d)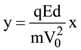 
17. Train A and train B are running on parallel tracks in the opposite directions with speeds of 36 km/hour and 72 km/hour, respectively. A person is walking in train A in the direction opposite to its motion with a speed of 1.8 km/hour. Speed (in ms–1) of this person as observed from train B will be close to:
(a) 29.5 ms−1
(b) 30.5 ms−1
(c) 31.5 ms−1
(d) 28.5 ms−1
18. Shown in the figure is rigid and uniform one meter long rod AB held in horizontal position by two strings tied to its ends and attached to the ceiling. The rod is of mass `m` and has another weight of mass 2 m hung at a distance of 75 cm from A. The tension in the string at A is:
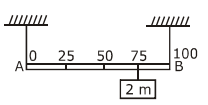
(a) 0.75 mg
(b) 0.5 mg
(c) 1 mg
(d) 2 mg
19. The least count of the main scale of a vernier callipers is 1 mm. Its vernier scale is divided into 10 divisions and coincide with 9 divisions of the main scale. When jaws are touching each other, the 7th division of vernier scale coincides with a division of main scale and the zero of vernier scale is lying right side of the zero of main scale. When this vernier is used to measure length of a cylinder the zero of the vernier scale between 3.1 cm and 3.2 cm and 4th VSD coincides with a main scale division. The length of the cylinder is: (VSD is vernier scale division)
(a) 3.21 cm
(b) 3.07 cm
(c) 2.99 cm
(d) 3.2 cm
20. A particle of mass m with an initial velocity 
collides perfectly elastically with a mass 3m at rest. It moves with a velocity 
after collision, then v is given by:
(a)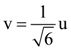 
(b)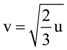 
(c) 
(d)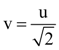 
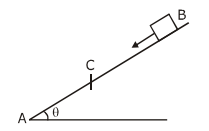
21. A small block starts slipping down from a point B on an inclined plane AB, which is making an angle θ with the horizontal section BC is smooth and the remaining section CA is rough with a coefficient of friction. It is found that the block comes to rest as it reaches the bottom (point A) of the inclined plane. If BC = 2AC, the coefficient of friction is given by μ =k tan θ. The value of k is __________
22. An engine takes in 5 moles of air at 20°C and 1atm, and compresses it adiabaticaly to 1/10th of the original volume. Assuming air to be a diatomic ideal gas made up of rigid molecules, the change in its internal energy during this process comes out to be X kJ. The value of X to the nearest integer is ___________.
23. When radiation of wavelength λ is used to illuminate a metallic surface, the stopping potential is V. When the same surface is illuminated with radiation of wavelength 3 λ, the stopping potential is V/4. If the threshold wavelength for the metallic surface is n λ then value of n will be __________.
24. A circular coil of radius 10 cm is placed in uniform magnetic field of 3.0 × 10–5 T with its plane perpendicular to the field initially. It is rotated at constant angular speed about an axis along the diameter of coil and perpendicular to magnetic field so that it undergoes half of rotation in 0.2s. The maximum value of EMF induced (in μV) in the coil will be close to the integer __________.
25. A 5μF capacitor is charged fully by a 220V supply. It is then disconnected from the supply and is connected in series to another uncharged 2.5μF capacitor. If the energy change during the charge redistribution is (X/100) J then value of X to the nearest integer is _________.
Chemistry
1. The increasing order of the following compounds towards HCN addition is:
(1) (iii) < (i) < (iv) < (ii)
(2) (iii) < (iv) < (i) < (ii)
(3) (i) < (iii) < (iv) < (ii)
(4) (iii) < (iv) < (ii) < (i)
2. Which of the following is used for the preparation of colloids?
(1) Van Arkel Method
(2) Ostwald Process
(3) Mond Process
(4) Bredig’s Arc Method
3. An open beaker of water in equilibrium with water vapour is in a sealed container. When a few grams of glucose are added to the beaker of water, the rate at which water molecules:
(1) leaves the vapour increases
(2) leaves the solution increases
(3) leaves the vapour decreases
(4) leaves the solution decreases
4. For octahedral Mn(II) and tetrahedral Ni(II) complexes, consider the following statements:
(I) both the complexes can be high spin.
(II) Ni(II) complexes can very rarely be low spin.
(III) with strong field ligands, Mn(II) complexes can be low spin.
(IV) the aqueous solution of Mn(II) ions is yellow in colour.
The correct statements are:
(1) (I), (III) and (IV) only
(2) (I), (II) and (III) only
(3) (II), (III) and (IV) only
(4) (I) and (II) only
5. The statement that is not true about ozone is:
(1) in the stratosphere, it forms a protective shield against UV radiation.
(2) in the atmosphere, it is depleted by CFCs.
(3) in the stratosphere, CFCs release chlorine-free radicals (Cl) which reacts with O3 to give chlorine dioxide radicals.
(4) it is a toxic gas and its reaction with NO gives NO2.
6. Consider the following reactions:
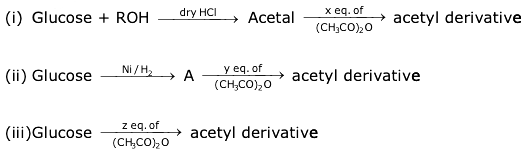
‘x’, ‘y’ and ‘z’ in these reactions are respectively.
(1) 4, 5 & 6
(2) 5, 4 & 5
(3) 5, 6 & 5
(4) 4, 6 & 5
7. The IUPAC name for the following compound is:
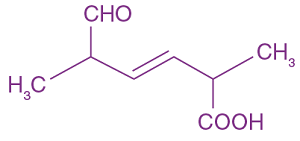
(1) 2,5-dimethyl-5-carboxy-hex-3-enal
(2) 2,5-dimethyl-6-oxo-hex-3-enoic acid
(3) 6-formyl-2-methyl-hex-3-enoic acid
(4) 2,5-dimethyl-6-carboxy-hex-3-enal
8. For the following Assertion and Reason, the correct option is
Assertion (A): When Cu (II) and Sulphide ions are mixed, they react together extremely quickly to give a solid.
Reason (R): The equilibrium constant of Cu2+ (aq) + S2– (aq) ⇌ CuS (s) is high because the solubility product is low.
(1) (A) is false and (R) is true.
(2) Both (A) and (R) are false.
(3) Both (A) and (R) are true but (R) is not the explanation for (A).
(4) Both (A) and (R) are true but (R) is the explanation for (A).
9. Which one of the following graphs is not correct for an ideal gas?
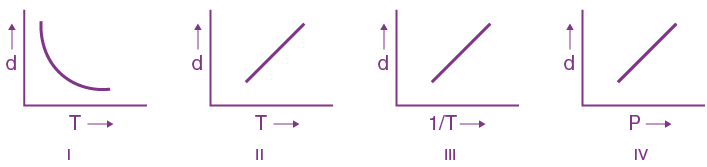
d = Density, P = Pressure, T = Temperature
The correct statements are:
(1) (i)
(2) (iv)
(3) (iii)
(4) (ii)
10. While titrating dilute HCl solution with aqueous NaOH, which of the following will not be required?
(1) Bunsen burner and measuring cylinder
(2) Burette and porcelain tile
(3) Clamp the phenolphthalein
(4) Pipette and distilled water
11. In Carius’ method of estimation of halogen, 0.172 g of an organic compound showed the presence of 0.08 g of bromine. Which of these is the correct structure of the compound?
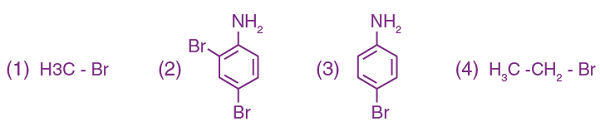
12. On heating compound (A) gives a gas (B) which is a constituent of air. This gas when treated with H2 in the presence of a catalyst gives another gas (C) which is basic in nature. (A) should not be:
(1) (NH4)2Cr2O7
(2) NaN3
(3) NH4NO2
(4) Pb(NO3)2
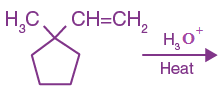
13. The major product in the following reaction is:
14. In general, the property (magnitudes only) that shows an opposite trend in comparison to other properties across a period is:
(1) Ionization enthalpy
(2) Electronegativity
(3) Atomic radius
(4) Electron gain enthalpy
15. The figure that is not a direct manifestation of the quantum nature of atoms is:
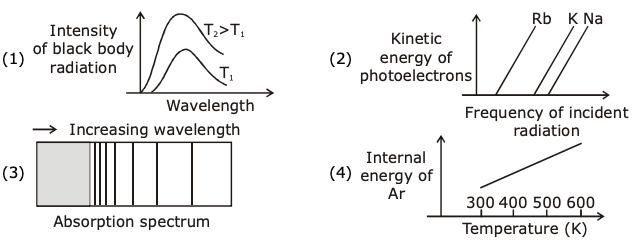
16. The major aromatic product C in the following reaction sequence will be:
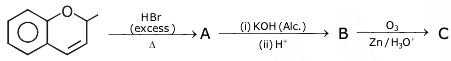
17. Consider that a d6 metal ion (M2+) forms a complex with aqua ligands, and the spin only magnetic moment of the complex is 4.90 BM. The geometry and the crystal field stabilization energy of the complex is:
(1) tetrahedral and –0.6Δt
(2) tetrahedral and –1.6Δt + 1P
(3) octahedral and –1.6Δ0
(4) octahedral and –2.4Δ0 + 2P
18. If AB4 molecule is a polar molecule, a possible geometry of AB4 is:
(1) Square planar
(2) Tetrahedral
(3) Square pyramidal
(4) Rectangular planar
19. Which of the following compounds will show retention in the configuration on nucleophilic substitution by OH– ion?
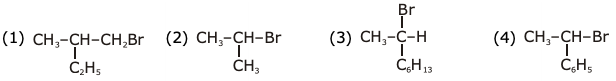
20. The metal mainly used in devising photoelectric cells is:
(1) Li
(2) Cs
(3) Rb
(4) Na
21. The mass of gas adsorbed, x, per unit mass of adsorbate, m, was measured at various pressures, p. A graph between log [x / m] and log p gives a straight line with slope equal to 2 and the intercept equal to 0.4771. The value of [x / m] at a pressure of 4 atm is: (Given log 3 = 0.4771)
22. The Gibbs energy change (in J) for the given reaction at [Cu2+] = [Sn2+] = 1 M and 298 K is:
Cu(s) + Sn2+ (aq.) → Cu2+(aq.) + Sn(s)
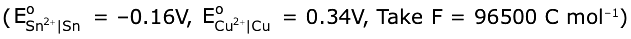
23. The internal energy change (in J) when 90 g of water undergoes complete evaporation at 100ºC is __________.
(Given: ΔHvap for water at 373 K = 41 kJ/mol, R = 8.314 JK–1 mol–1)
24. The oxidation states of iron atoms in compounds (A), (B) and (C), respectively, are x, y and z. The sum of x, y and z is _____.
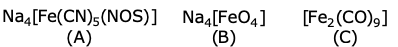
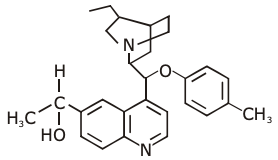
25. The number of chiral carbons present in the molecule given below is ________.
Mathematics
1. A line parallel to the straight line 2x – y = 0 is tangent to the hyperbola 
at the point (x1, y1). Then 
is equal to :
(1) 6
(2) 10
(3) 8
(4) 5
2. The domain of the function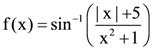 
is (−∞, −a] ∪ [a, ∞). Then a is equal to :
(1) 
(2) 
(3) 
(4) 
3. If a function f(x) defined by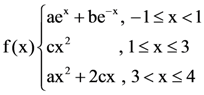 
be continuous for some a, b, c ∈ R and f´(0) + f´(2) = e, then the value of a is:
(1) 
(2) 
(3) 
(4) 
4. The sum of the first three terms of a G.P. is S and their product is 27. Then all such S lie in
(1) (−∞,−9]∪[3, ∞)
(2) [−3, ∞)
(3) (−∞,−9]
(4) (−∞,−3]∪[9, ∞)
5. If R = {(x,y) : x,y ∈ Z, x2 + 3y2 ≤ 8} is a relation on the set of integers Z, then the domain of R−1 is:
(1) {−1, 0, 1}
(2) {−2, −1, 1, 2}
(3) {0,1}
(4) {-2,-1,0,1,2}
6. The value of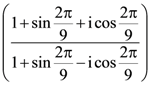 
is :
(1) 
(2) 
(3) 
(4) 
7. Let P(h, k) be a point on the curve y = x2 + 7x + 2, nearest to the line, y = 3x – 3. Then the equation of the normal to the curve at P is:
(1) x + 3y – 62 = 0
(2) x – 3y – 11 = 0
(3) x – 3y + 22 = 0
(4) x + 3y + 26 = 0
8. Let A be a 2×2 real matrix with entries from {0,1} and A ≠ 0. Consider the following two statements:
(P) If A ≠I2, then A = -1
(Q) If A =1, then tr(A) = 2,
where I2 denotes 2 × 2 identity matrix and tr(A) denotes the sum of the diagonal entries of A. Then:
(1) Both (P) and (Q) are false
(2) (P) is true and (Q) is false
(3) Both (P) and (Q) are true
(4) (P) is false and (Q) is true
9. Box I contains 30 cards numbered 1 to 30 and Box II contains 20 cards numbered 31 to 50. A box is selected at random and a card is drawn from it. The number on the card is found to be a non-prime number. The probability that the card was drawn from Box I is:
(1) 4/17
(2) 8/17
(3) 2/5
(4) 2/3
10. If p(x) be a polynomial of degree three that has a local maximum value 8 at x = 1 and a local minimum value 4 at x = 2; then p(0) is equal to :
(1) 12
(2) −12
(3) −24
(4) 6
11. The contra positive of the statement “If I reach the station in time, then I will catch the train” is:
(1) If I will catch the train, then I reach the station in time.
(2) If I do not reach the station in time, then I will catch the train.
(3) If I do not reach the station in time, then I will not catch the train.
(4) If I will not catch the train, then I do not reach the station in time.
12. Let α and β be the roots of the equation, 5x2 + 6x − 2 = 0. If Sn = αn + βn, n = 1,2,3,.. then:
(1) 5S6 + 6S5 + 2S4 = 0
(2) 6S6 + 5S5 = 2S4
(3) 6S6 + 5S5 + 2S4 = 0
(4) 5S6 + 6S5 = 2S4
13. If the tangent to the curve y = x+sin y at a point (a,b) is parallel to the line joining (0, 3/2) and (1/2, 2), then:
(1) b = (π/2) + a
(2) |a + b| = 1
(3) |b – a| = 1
(4) b = a
14. Area (in sq. units) of the region outside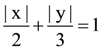 
and inside the ellipse 
is:
(1) 3(π – 2)
(2) 6(π – 2)
(3) 6(4 – π)
(4) 3(4 – π)
15. If |x| < 1, |y| < 1 and x ≠ y, then the sum of infinity of the following series (x + y) + (x2 + + xy + y2) + (x3 + x2y + xy2 + y3)+… is:
(1) 
(2) 
(3) 
(4) 
16. Let α > 0, β > 0 be such that α3 + β2 = 4. If the maximum value of the term independent of x in the binomial expansion of (αx1/9 + βx1/6)10 is 10k, then k is equal to:
(1) 176
(2) 336
(3) 352
(4) 84
17. Let S be the set of all λ ∈ R for which the system of linear equations
2x – y + 2z = 2
x – 2y + λz = −4
x + λy + z = 4
has no solution. Then the set S
(1) is an empty set.
(2) is a singleton.
(3) contains more than two elements.
(4) contains exactly two elements.
18. Let X = {x ∈ N: 1 ≤ x ≤ 17} and Y = {ax + b : x ∈ X and a, b ∈ R, a > 0}. If mean and variance of elements of Y are 17 and 216 respectively then a + b is equal to:
(1) −27
(2) 7
(3) −7
(4) 9
19. Let y = y(x) be the solution of the differential equation, 
If y(π) = a, and dy/dx at x = π is b, then the ordered pair (a, b) is equal to :
(1) (2, 3/2)
(2) (1, 1)
(3) (2, 1)
(4) (1, −1)
20. The plane passing through the points (1,2,1), (2,1,2) and parallel to the line, 2x = 3y, z = 1 also passes through the point:
(1) (0, −6, 2)
(2) (0, 6, −2)
(3) (−2, 0, 1)
(4) (2, 0, −1)
21. The number of integral values of k for which the line, 3x + 4y = k intersects the circle, x2 + y2 − 2x – 4y + 4 = 0 at two distinct points is…
22. Let 
be three unit vectors such that 
Then 
is equal to:
23. If the letters of the word ’MOTHER’ be permuted and all the words so formed (with or without meaning) be listed as in a dictionary, then the position of the word ’MOTHER’ is….
24. If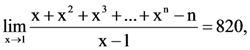 
(n ∈ N) then the value of n is equal to:
25. The integral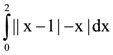 
is equal to:
Latest Govt Job & Exam Updates: