Physics
1. Starting from the origin at time t = 0, with initial velocity 
a particle moves in the x-y plane with a constant acceleration of 
At time t, its coordinates are (20 m, y0 m). The values of t and y0 are, respectively:
(1) 5s and 25 m
(2) 2s and 18 m
(3) 2s and 24 m
(4) 4s and 52 m
2. A small bar magnet placed with its axis at 30° with an external field of 0.06 T experiences a torque of 0.018 Nm. The minimum work required to rotate it from its stable to unstable equilibrium position is:
(1) 7.2 × 10−2 J
(2) 6.4 × 10−2 J
(3) 9.2 × 10−3 J
(4) 11.7 × 10−3 J
3.Choose the correct option relating wave lengths of different parts of electromagnetic wave spectrum:
(1) λradio waves > λmicro waves > λvisible > λx-rays
(2) λvisible > λx-rays > λradio waves > λmicro waves
(3) λvisible < λmicro waves < λradio waves < λx-rays
(4) λx-rays < λmicro waves < λradio waves < λvisible
4. On the x-axis and at a distance x from the origin, the gravitational field due a mass distribution is given by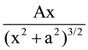 
in the x-direction. The magnitude of gravitational potential on the x-axis at a distance x, taking its value to be zero at infinity, is:
(1) A(x2 + a2)3/2
(2) 
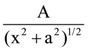
(3) A(x2 + a2)1/2
(4) 
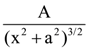
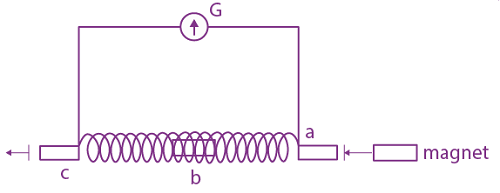
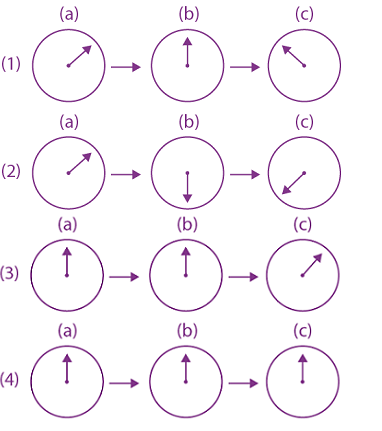
5. A small bar magnet is moved through a coil at constant speed from one end to the other. Which of the following series of observations will be seen on the galvanometer G attached across the coil?
6. A battery of 3.0V is connected to a resistor dissipating 0.5 W of power. If the terminal voltage of the battery is 2.5V, the power dissipated within the internal resistance is:
(1) 0.072 W
(2) 0.10 W
(3) 0.125 W
(4) 0.50 W
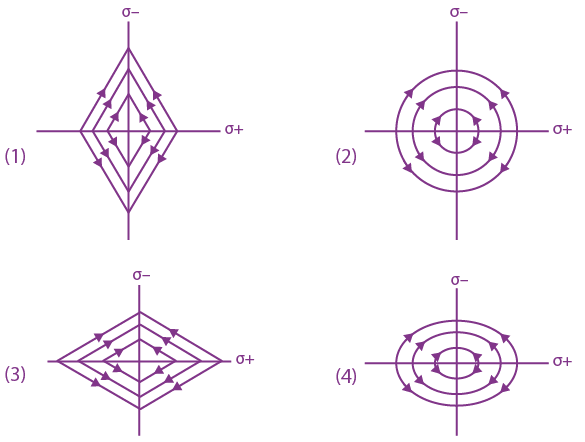
7. Two charged thin infinite plane sheets of uniform surface charge density σ + and σ –, where| σ+| > |σ–|, intersects at right angle. Which of the following best represents the electric field lines for this system?
8. An air bubble of radius 1 cm in water has an upward acceleration 9.8 cm s–2. The density of water is 1 gm cm–3 and water offers negligible drag force on the bubble. The mass of the bubble is (g = 980 cm/s2).
(1) 1.52 gm
(2) 4.51 gm
(3) 3.15 gm
(4) 4.15 gm
9. A wire A, bent in the shape of an arc of a circle, carrying a current of 2A and having radius 2 cm and another wire B, also bent in the shape of arc of a circle, carrying a current of 3 A and having radius of 4 cm, are placed as shown in the figure. The ratio of the magnetic field due to the wires A and B at the common centre O is:
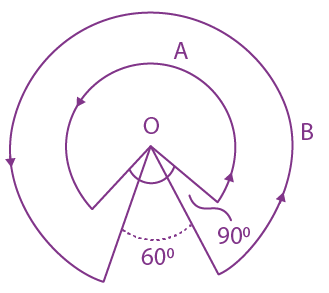
(1) 2 : 5
(2) 6 : 5
(3) 6 : 4
(4) 4 : 6
10. Particle A of mass mA=m/2 moving along the x-axis with velocity v0 collides elastically with another particle B at rest having mass mB = m/3. If both particles move along the x-axis after the collision, the change ∆λ in de-Broglie wavelength of particle A, in terms of its de-Broglie wavelength (λ0) before collision is:
(1) 
(2) ∆λ = 2λ0
(3) ∆λ = 4λ0
(4) 
11. Blocks of masses m, 2m, 4m and 8m are arranged in a line on a frictionless floor. Another block of mass m, moving with speed v along the same line (see figure) collides with mass m in perfectly inelastic manner. All the subsequent collisions are also perfectly inelastic. By the time the last block of mass 8m starts moving the total energy loss is p% of the original energy. Value of ‘p’ is close to:
(1) 94
(2) 87
(3) 37
(4) 77
12. Given figure shows few data points in a photo-electric effect experiment for a certain metal. The minimum energy for ejection of electron from its surface is: (Planck’s constant h = 6.62 × 10–34s)
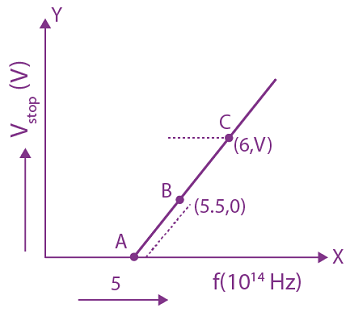
(1) 2.10 eV
(2) 2.27 eV
(3) 2.59 eV
(4) 1.93 eV
13. The specific heat of water = 4200 J kg–1K–1 and the latent heat of ice = 3.4 × 105 J kg−1.100 grams of ice at 0°C is placed in 200 g of water at 25°C. The amount of ice that will melt as the temperature of water reaches 0°C is close to (in grams):
(1) 63.8
(2) 64.6
(3) 61.7
(4) 69.3
14. A beam of plane polarised light of large cross-sectional area and uniform intensity of 3.3 Wm–2 falls normally on a polariser (cross sectional area 3 × 10–4 m2) which rotates about its axis with an angular speed of 31.4 rad/s. The energy of light passing through the polariser per revolution is close to:
(1) 1.0 × 10−4 J
(2) 1.0 × 10−5 J
(3) 5.0 × 10−4 J
(4) 1.5 × 10−4 J
15. For a transverse wave travelling along a straight line, the distance between two peaks (crests) is 5m, while the distance between one crest and one trough is 1.5m. The possible wavelengths (in m) of the waves are:
(1) 1, 3, 5,…..
(2) 1, 2, 3,……
(3) 1/2, 1/4, 1/6…..
(4) 1/1, 1/3, 1/5…..
16. Match the CP/CV ratio for ideal gases with different type of molecules:
17. Two points charges 4q and –q are fixed on the x-axis at x = −(d/2) and x = (d/2), respectively. If a third point charge ‘q’ is taken from the origin to x = d along the semicircle as shown in the figure, the energy of the charge will:
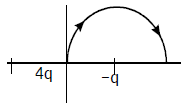
(1) decrease by q2/4π∈0d
(2) decrease by 4q2/3π∈0d
(3) increase by 3q2/4π∈0d
(4) increase by 2q2/3π∈0d
18. A Tennis ball is released from a height h and after freely falling on a wooden floor it rebounds and reaches height h/2. The velocity versus height of the ball during its motion may be represented graphically by: (graphs are drawn schematically and are not to scale)
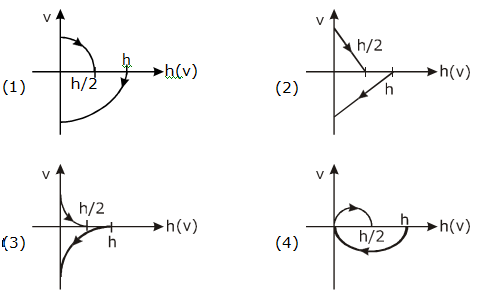
19. Dimensional formula for thermal conductivity is (here K denotes the temperature):
(1) MLT−3K−1
(2) MLT−2K−2
(3) MLT−2K
(4) MLT−3K
20. Take the breakdown voltage of the zener diode used in the given circuit as 6V. For the input voltage shown in figure below, the time variation of the output voltage is : (Graphs drawn are schematic and not to scale)
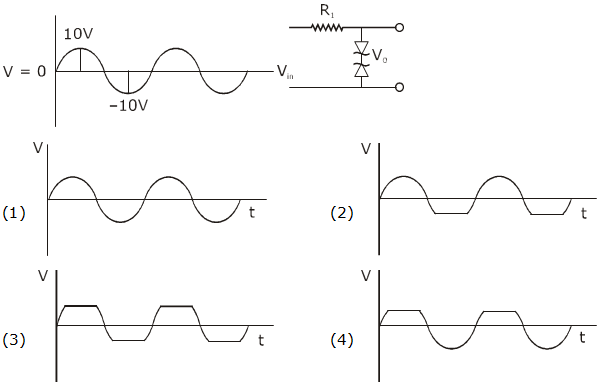
21. In the line spectra of hydrogen atoms, difference between the largest and the shortest wavelengths of the Lyman series is 304Å. The corresponding difference for the Paschen series in Å is : ___________.
22. A closed vessel contains 0.1 mole of a monoatomic ideal gas at 200 K. If 0.05 mole of the same gas at 400 K is added to it, the final equilibrium temperature (in K) of the gas in the vessel will be close to _______.
23. ABC is a plane lamina of the shape of an equilateral triangle. D, E are mid points of AB, AC and G is the centroid of the lamina. Moment of inertia of the lamina about an axis passing through G and perpendicular to the plane ABC is I0. If part ADE is removed, the moment of inertia of the remaining part about the same axis is NI0 /16 where N is an integer. Value of N is _____________.
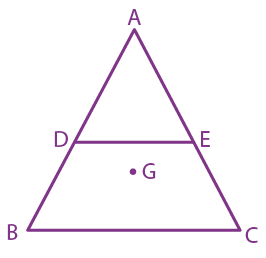
24. In a compound microscope, the magnified virtual image is formed at a distance of 25 cm from the eye-piece. The focal length of its objective lens is 1 cm. If the magnification is 100 and the tube length of the microscope is 20 cm, then the focal length of the eyepiece lens (in cm) is __________.
25. A circular disc of mass M and radius R is rotating about its axis with angular speed ω1. If another stationary disc having radius R/2 and same mass M is dropped co-axially on to the rotating disc. Gradually both discs attain constant angular speed ω2. The energy lost in the process is p% of the initial energy. Value of p is __________.
Chemistry
1. The IUPAC name of the following compound is:
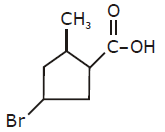
(1) 3-Bromo-5-methyl cyclopentane carboxylic acid
(2) 4-Bromo-2-methyl cyclopentane carboxylic acid
(3) 5-Bromo-3-methyl cyclopentanoic acid
(4) 3-Bromo-5-methyl cyclopentanoic acid
2. On heating, lead(II) nitrate gives a brown gas (A). The gas (A) on cooling changes to a colourless solid/liquid (B). (B) on heating with NO changes to a blue solid (C). The oxidation number of nitrogen in solid (C) is:
(1) +3
(2) +4
(3) +2
(4) +5
3. The ionic radii of O2–, F–, Na+ and Mg2+ are in the order:
(1) F– > O2– > Na+ > Mg2+
(2) Mg2+ > Na+ > F− > O2−
(3) O2– > F– > Na+ > Mg2+
(4) O2– > F– > Mg2+ > Na+
4. When neopentyl alcohol is heated with an acid, it is slowly converted into an 85:15 mixture of alkenes A and B, respectively. What are these alkenes?
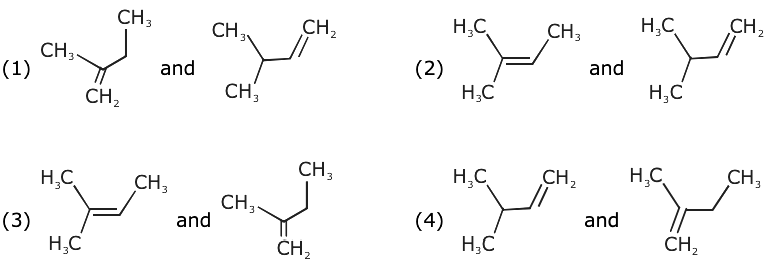
5. The region in the electromagnetic spectrum where the Balmer series lines appear is:
(1) Microwave
(2) Infrared
(3) Ultraviolet
(4) Visible
6. Identify the incorrect statement from the options below for the above cell:
(1) If Eext = 1.1 V, no flow of e– or current occurs
(2) If Eext > 1.1 V, Zn dissolves at Zn electrode and Cu deposits at Cu electrode
(3) If Eext > 1.1 V, e– flow from Cu to Zn
(4) If Eext < 1.1 V, Zn dissolves at the anode and Cu deposits at the cathode
7. What are the functional groups present in the structure of maltose?
(1) One acetal and one hemiacetal
(2) One acetal and one ketal
(3) One ketal and one hemiketal
(4) Two acetals
8. Match the following:
(i) Foam (a) smoke
(ii) Gel (b) cell fluid
(iii) Aerosol (c) jellies
(iv) Emulsion (d) rubber
(e) froth
(f) milk
(1) (i)-(e), (ii)-(c), (iii)-(a), (iv)-(f)
(2) (i)-(b), (ii)-(c), (iii)-(e), (iv)-(d)
(3) (i)-(d), (ii)-(b), (iii)-(a), (iv)-(e)
(4) (i)-(d), (ii)-(b), (iii)-(e), (iv)-(f)
9. An organic compound (A) (molecular formula C6H12O2) was hydrolysed with dilute H2SO4 to give a carboxylic acid (B) and alcohol (C). ‘C’ gives white turbidity immediately when treated with anhydrous ZnCl2 and conc. HCl. The organic compound (A) is:
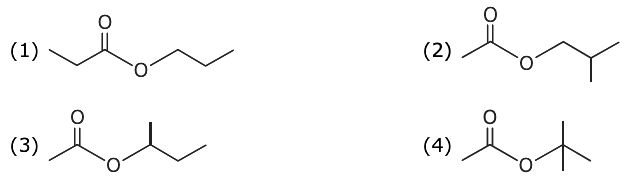
10. Among the statements (a)-(d), the correct ones are:
(a) Limestone is decomposed to CaO during the extraction of iron from its oxides.
(b) In the extraction of silver, silver is extracted as an anionic complex.
(c) Nickel is purified by Mond’s process.
(d) Zr and Ti are purified by Van Arkel method.
(1) (c) and (d) only
(2) (b), (c) and (d) only
(3) (a), (b), (c) and (d)
(4) (a), (c) and (d) only
11. For one mole of an ideal gas, which of these statements must be true?
(a) U and H each depends only on temperature
(b) Compressibility factor z is not equal to 1
(c) CP,m – CV,m = R
(d) dU = CV dT for any process
(1) (a), (c) and (d)
(2) (a) and (c)
(3) (c) and (d)
(4) (b), (c) and (d)
12. [P] on treatment with Br2/FeBr3 in CCl4 produced a single isomer C8H7O2Br while heating [P] with soda lime gave toluene. The compound [P] is:
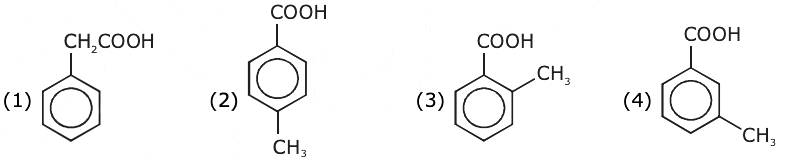
13. For the equilibrium A ⇌ B the variation of the rate of the forward (a) and reverse (b) reaction with time is given by :
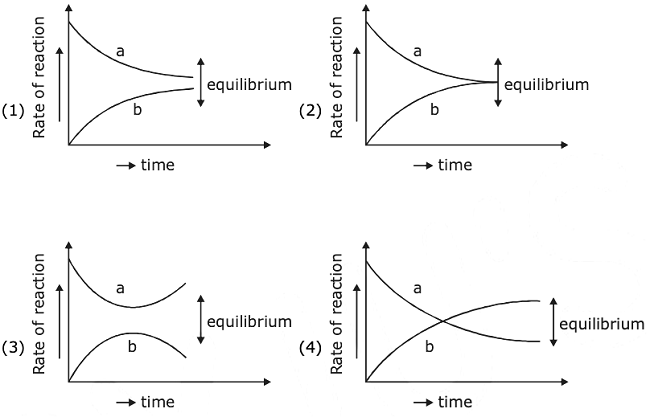
14. The pair in which both the species have the same magnetic moment (spin only) is:
(1) [Co(OH)4]2– and [Fe(NH3)6]2+
(2) [Mn(H2O)6]2+ and [Cr(H2O)]2+
(3) [Cr(H2O)6]2+ and [CoCl4]2–
(4) [Cr(H2O)6]2+ and [Fe(H2O)6]2+
15. The number of isomers possible for [Pt(en)(NO2)2] is:
(1) 2
(2) 3
(3) 4
(4) 1
16. The decreasing order of reactivity of the following organic molecules towards the AgNO3 solution is:
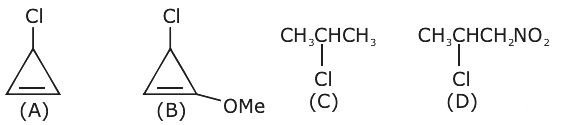
(1) (B) > (A) > (C) > (D)
(2) (A) > (B) > (C) > (D)
(3) (A) > (B) > (D) > (C)
(4) (C) > (D) > (A) > (B)
17. The intermolecular potential energy for the molecules A, B, C and D given below suggests that:
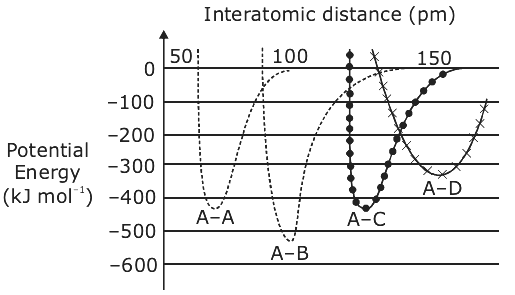
(1) A–A has the largest bond enthalpy.
(2) D is more electronegative than other atoms.
(3) A–D has the shortest bond length.
(4) A–B has the stiffest bond.
18. Which of the following will react with CHCl3 + alc. KOH?
(1) Thymine and proline
(2) Adenine and thymine
(3) Adenine and lysine
(4) Adenine and proline
19. The elements with atomic numbers 101 and 104 belong to, respectively:
(1) Actinoids and Group 6
(2) Group 11 and Group 4
(3) Group 6 and Actinoids
(4) Actinoids and Group 4
20. On combustion of Li, Na and K in excess of air, the major oxides formed, respectively, are :
(1) Li2O2, Na2O2 and K2O2
(2) Li2O, Na2O2 and KO2
(3) Li2O, Na2O and K2O2
(4) Li2O, Na2O2 and K2O
21. The number of chiral centres present in [B] is ________.
22. At 300 K, the vapour pressure of a solution containing 1 mole of n-hexane and 3 moles of n-heptane is 550 mm of Hg. At the same temperature, if one more mole of n-heptane is added to this solution, the vapour pressure of the solution increases by 10 mm of Hg. What is the vapour pressure in mm of Hg of n-heptane in its pure state _______?
23. The mass of ammonia in grams produced when 2.8 kg of dinitrogen quantitatively reacts with 1 kg of dihydrogen is _________.
24. If 75% of a first order reaction was completed in 90 minutes, 60% of the same reaction would be completed in approximately (in minutes) ________. (take : log 2 = 0.30; log 2.5 = 0.40)
25. A 20.0 mL solution containing 0.2 g impure H2O2 reacts completely with 0.316 g of KMnO4 in acid solution. The purity of H2O2 (in %) is _______ (mol. wt. of H2O2 = 34’ mole wt. of KMnO4 = 158)
Mathematics
1. Let y = y(x) be the solution of the differential equation, xy’− y = x2(x cos x + sin x), x > 0. If y(π) = π, then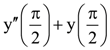 
is equal to
(1) 
(2) 
(3) 
(4) 
2. The value of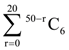 
is equal to:
(1) 51C7 – 30C7
(2) 51C7 + 30C7
(3) 50C7 – 30C7
(4) 50C6 – 30C6
3. Let [t] denote the greatest integer ≤ t. Then the equation in x, [x]2 + 2[x + 2] − 7 = 0 has:
(1) exactly four integral solutions.
(2) infinitely many solutions.
(3) no integral solution.
(4) exactly two solutions.
4. Let P(3, 3) be a point on the hyperbola, 
If the normal to it at P intersects the x-axis at (9, 0) and e is its eccentricity, then the ordered pair (a2, e2) is equal to:
(1) (9, 3)
(2) (9/2, 2)
(3) (9/2, 3)
(4) (3/2, 2)
5. Let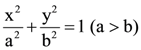 
be a given ellipse, length of whose latus rectum is 10. If its eccentricity is the maximum value of the function, 
then a2 + b2 is equal to
(1) 135
(2) 116
(3) 126
(4) 145
6. Let 
Then f(3) – f(1) is equal to:
(1) 
(2) 
(3) 
(4) 
7. If 1 + (1 − 22 × 1) + (1 − 42 × 3) + (1 − 62 × 5) + …… + (1 − 202 × 19) = α – 220 β, then an ordered pair (α, β) is equal to:
(1) (10, 97)
(2) (11, 103)
(3) (11, 97)
(4) (10, 103)
8. The integral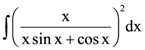 
is equal to
(where C is a constant of integration):
(1) 
(2) 
(3) 
(4) 
9. Let f(x) = |x – 2| and g(x) = f(f(x)), x ∈ [0, 4]. Then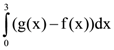 
is equal to:
(1) 1/2
(2) 0
(3) 1
(4) 3/2
10. Let x0 be the point of local maxima of 
where 
and 
Then the value of 
at x = x0 is :
(1) 2
(2) −4
(3) −30
(4) 14
11. A triangle ABC lying in the first quadrant has two vertices as A(1, 2) and B(3, 1). If ∠BAC = 90° and ar(ΔABC) = 5√5 s units, then the abscissa of the vertex C is:
(1) 1 + √5
(2) 1 + 2√5
(3) 2√5 − 1
(4) 2 + √5
12. Let f be a twice differentiable function on (1,6). If f(2) = 8, f´(2) = 5, f´(x) ≥ 1 and f´´(x) ≥ 4, for all x ∈ (1, 6), then:
(1) f(5) + f´(5) ≥ 28
(2) f´(5) + f´´(5) ≤ 20
(3) f(5) ≤ 10
(4) f(5) + f´(5) ≤ 26
13. Let α and β be the roots of x2 − 3x + p = 0 and γ and δ be the roots of x2 − 6x + q = 0. If α, β, γ, δ form a geometric progression. Then ratio (2q + p): (2q − p) is:
(1) 33: 31
(2) 9: 7
(3) 3 : 1
(4) 5 :3
14. Let 
z = x + iy and k > 0. If the curve represented by Re(u) + Im(u) =1 intersects the y-axis at the points P and Q where PQ =5, then the value of k is:
(1) 4
(2) 1/2
(3) 2
(4) 3/2
15. If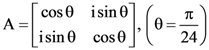 
and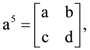 
where i = √−1 then which one of the following is not true?
(1) a2 – d2 = 0
(2) a2 – c2 = 1
(3) 0 ≤ a2 + b2 ≤ 1
(4) a2 – b2 = 1/2
16. The mean and variance of 8 observations are 10 and 13.5, respectively. If 6 of these observations are 5, 7, 10, 12, 14, 15, then the absolute difference of the remaining two observations is:
(1) 3
(2) 9
(3) 7
(4) 5
17. A survey shows that 63% of the people in a city read newspaper A whereas 76% read newspaper B. If x% of the people read both the newspapers, then a possible value of x can be:
(1) 37
(2) 29
(3) 65
(4) 55
18. Given the following two statements
(S1): (q˅p)→(p ↔ ~q) is a tautology.
(S2): ~q ˄ (~p ↔ q) is a fallacy. Then:
(1) only (S1) is correct.
(2) both (S1) and (S2) are correct.
(3) only (S2) is correct
(4) both (S1) and (S2) are not correct.
19. Two vertical poles AB = 15 m and CD = 10 m are standing apart on a horizontal ground with points A and C on the ground. If P is the point of intersection of BC and AD, then the height of P (in m) above the line AC is:
(1) 5
(2) 20/3
(3) 10/3
(4) 6
20. If (a + √2b cos x)( a − √2b cos y) = a2 − b2, where a > b > 0, then 
is:
(1) 
(2) 
(3) 
(4) 
21. Suppose a differentiable function f(x) satisfies the identity f(x + y) = f(x) + f(y) + xy2 + x2y,for all real x and y. If 
then f´(3) is equal to…………
22. If the equation of a plane P, passing through the intersection of the planes, x + 4y – z + 7 = 0 and 3x + y + 5z = 8 is ax + by + 6z = 15 for some a, b ∈ R, then the distance of the point (3, 2, −1) from the plane P is ….. units.
23. If the system of equations
x – 2y + 3z = 9
2x + y + z = b
x – 7y + az = 24, has infinitely many solutions, then a – b is equal to…………..
24. Let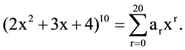 
Then a7/a13 is equal to………..
25. The probability of a man hitting a target is 1/10. The least number of shots required, so that the probability of his hitting the target at least once is greater than 1/4 is……….
Latest Govt Job & Exam Updates: