Physics
Section-A
1. A 5V battery is connected across the points X and Y. Assume D1 and D2 to be normal silicon diodes. Find the current supplied by the battery if the + ve terminal of the battery is connected to point X.
(a) ~0.86 A
(b) ~0.5 A
(c) ~0.43 A
(d) ~1.5 A
2. A solid sphere of radius R gravitationally attracts a particle placed at 3R from its centre with a force F1. Now a spherical cavity of radius R/2 is made in the sphere (as shown in figure) and the force becomes F2. The value of F1: F2 is:
(a) 41 : 50
(b) 36 : 25
(c) 50 : 41
(d) 25 : 36
3. A student is performing the experiment of resonance column. The diameter of the column tube is 6 cm. The frequency of the tuning fork is 504 Hz. Speed of the sound at the given temperature is 336 m/s. The zero of the metre scale coincides with the top end of the resonance column tube. The reading of the water level in the column when the first resonance occurs is:
(a) 13 cm
(b) 14.8 cm
(c) 16.6 cm
(d) 18.4 cm
4. A diatomic gas, having 
is heated at constant pressure. The ratio dU : dQ : dW
(a) 3 : 7 : 2
(b) 5 : 7 : 2
(c) 5 : 7 : 3
(d) 3 : 5 : 2
5. Statement I: A speech signal of 2 kHz is used to modulate a carrier signal of 1 MHz. The bandwidth requirement for the signal is 4 kHz.
Statement II: The side band frequencies are 1002 kHz and 998 kHz.
In the light of the above statements, choose the correct answer from the options given below:
(a) Both statement I and statement II are false
(b) Statement I is false but statement II is true
(c) Statement I is true but statement II is false
(d) Both statement I and statement II are true
6. The current (i) at time t = 0 and t = ∞ respectively for the given circuit is:
(a) 
(b) 
(c) 
(d) 
7. Two satellites A and B of masses 200 kg and 400 kg are revolving round the earth at height of 600 km and 1600 km respectively.
If TA and TB are the time periods of A and B respectively then the value of TB − TA:
[Given: Radius of earth = 6400 km, mass of earth = 6×1024 kg]
(a) 4.24 × 102 s
(b) 3.33 × 102 s
(c) 1.33 × 103 s
(d) 4.4 × 103 s
8. An engine of a train, moving with uniform acceleration, passes the signal post with velocity u and the last compartment with velocity v. The velocity with which middle point of the train passes the signal post is:
(a) 
(b) 
(c) 
(d) 
9. A proton, a deuteron and an α particle are moving with the same momentum in a uniform magnetic field. The ratio of magnetic forces acting on them is _______ and their speeds are in the ratio______.
(a) 2 : 1 : 1 and 4 : 2 : 1
(b) 1 : 2 : 4 and 2 : 1 :1
(c) 1 : 2 : 4 and 1 : 1 : 2
(d) 4 : 2 : 1 and 2 : 1 : 1
10. Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R.
Assertion A: When a rod lying freely is heated, no thermal stress is developed in it.
Reason R: On heating, the length of the rod increases
In the light of the above statements, choose the correct answer from the options given below:
(a) A is true but R is false
(b) Both A and R are true and R is the correct explanation of A
(c) Both A and R are true but R is NOT the correct explanation of A
(d) A is false but R is true
11. In an octagon ABCDEFGH of equal side, what is the sum of
(a) 
(b) 
(c) 
(d) 
12. Two radioactive substances X and Y originally have N1 and N2 nuclei respectively. Half-life of X is half of the half-life of Y. After three half-lives of Y, numbers of nuclei of both are equal. The ratio N1/N2 will be equal to:
(a) 8/1
(b) 1/8
(c) 3/1
(d) 1/3
13. Match List-I with List-II:
List-I List-II
(a) h(Planck’s constant) (i) [MLT−1]
(b) E(Kinetic energy) (ii) [ML2T−1]
(c) V(Electric potential) (iii) [ML2T−2]
(d) P (Linear momentum) (iv) [ML2I−1T−3]
Choose the correct answer from the options given below:
(a) (a) → (ii), (b) →(iii), (c) → (iv), (d) → (i)
(b) (a) →(i), (b) → (ii), (c) →(iv), (d) → (iii)
(c) (a) → (iii), (b) → (ii), (c) →(iv), (d) →(i)
(d) (a) → (iii), (b) → (iv), (c) →(ii), (d) →(i)
14. The pitch of the screw gauge is 1 mm and there are 100 divisions on the circular scale. When nothing is put in between the jaws, the zero of the circular scale lines 8 divisions below the reference line. When a wire is placed between the jaws, the first linear scale division is clearly visible while 72nd division on circular scale coincides with the reference line. The radius of the wire is:
(a) 1.64 mm
(b) 1.80 mm
(c) 0.82 mm
(d) 0.90 mm
15. If the time period of a two meter long simple pendulum is 2 s, the acceleration due to gravity at the place where pendulum is executing S.H.M. is:
(a) 2π2ms−2
(b) 16 m/s2
(c) 9.8 ms−2
(d) π2 ms−2
16. An α particle and a proton are accelerated from rest by a potential difference of 200 V. After this, their de Broglie wavelengths are λα and λp The ratio λp/λα is:
(a) 8
(b) 2.8
(c) 3.8
(d) 7.8
17. Given below are two statements: one is labelled as Assertion A and the other is labelled as reason R.
Assertion A: The escape velocities of planet A and B are same. But A and B are of unequal masses.
Reason R: The product of their masses and radii must be same. M1R1 = M2R2
In the light of the above statements, choose the most appropriate answer from the options given below:
(a) Both A and R are correct but R is NOT the correct explanation of A
(b) A is correct but R is not correct
(c) Both A and R are correct and R is the correct explanation of A
(d) A is not correct but R is correct
18. The angular frequency of alternating current in a L-C-R circuit is 100 rad/s. The components connected are shown in the figure. Find the value of inductance of the coil and capacity of condenser.
(a) 0.8 H and 250 μF
(b) 0.8 H and 150 μF
(c) 1.33 H and 250 μF
(d) 1.33 H and 150 μF
19. Two coherent light sources having intensities in the ratio 2x produce an interference pattern. The ratio 
will be:
(a) 
(b) 
(c) 
(d) 
20. Magnetic fields at two points on the axis of a circular coil at a distance of 0.05 m and 0.2 m from the centre are in the ratio 8 : 1. The radius of coil is ______
(a) 0.15 m
(b) 0.2 m
(c) 0.1 m
(d) 1.0 m
Section-B
21. The same size images are formed by a convex lens when the object is placed at 20 cm or at 10 cm from the lens. The focal length of a convex lens is ______ cm.
22. The electric field in a region is given by 
The ratio of flux of reported field through the rectangular surface of area 0.2 m2 (parallel to y-z plane) to that of the surface of area 0.3 m2 (parallel to x-z plane) is a : 2, where a = ________
[Here i, j and k are unit vectors along x, y and z-axes respectively]
23. 512 identical drops of mercury are charged to a potential of 2 V each. The drops are joined to form a single drop. The potential of this drop is ____ V.
24. The potential energy (U) of a diatomic molecule is a function dependent on r (interatomic distance) as 
Where, a and b are positive constants. The equilibrium distance between two atoms will (2α/β)a/b. Where a =_______
25. A small bob tied at one end of a thin string of length 1m is describing a vertical circle so that the maximum and minimum tension in the string are in the ratio 5 : 1. The velocity of the bob at the highest position is ______ m/s. (take g = 10 m/s2)
26. In a certain thermodynamic process, the pressure of a gas depends on its volume as kV3. The work done when the temperature changes from 1000 C to 300°C will be ______ nR, where n denotes number of moles of a gas.
27. In the given circuit of potentiometer, the potential difference E across AB (10 m length) is larger than E1 and E2 as well. For key K1 (closed), the jockey is adjusted to touch the wire at point J1 so that there is no deflection in the galvanometer. Now the first battery (E1) is replaced by the second battery (E2) for working by making K1 open and E2 The galvanometer gives then null deflection at J2. The value of E1/E2 is the smallest fraction of a/b, Then the value of a is ____.
28. A monoatomic gas of mass 4.0 u is kept in an insulated container. Container is moving with a velocity 30 m/s. If container is suddenly stopped then change in temperature of the gas (R=gas constant) is x/3R. Value of x is ______.
29. A coil of inductance 2 H having negligible resistance is connected to a source of supply whose voltage is given by V = 3t volt. (where t is in second). If the voltage is applied when t = 0, then the energy stored in the coil after 4 s is _______ J.
30. A transmitting station releases waves of wavelength 960 m. A capacitor of 256 μF is used in the resonant circuit. The self inductance of coil necessary for resonance is _____ × 10–8
Chemistry
Section-A
1. Ellingham diagram is a graphical representation of:
(a) ΔG vs T
(b) (ΔG – TΔS) vs T
(c) ΔH vs T
(d) ΔG vs P
2. Which of the following equations depicts the oxidizing nature of H2O2?
(a) Cl2 + H2O2 → 2HCl + O2
(b) KlO4 + H2O2 → KlO3 + H2O + O2
(c) 2l– + H2O2 + 2H+ → I2 + 2H2O
(d) I2 + H2O2 + 2OH– → 2I– + 2H2O + O2
3. In Freundlich adsorption isotherm at moderate pressure, the extent of adsorption (x/m) is directly proportional to Px. The value of x is:
(a) ∞
(b) 1
(c) zero
(d) 1/n
4. According to molecular orbital theory, the species among the following that does not exist is:
(a) He2−
(b) He2+
(c) O22−
(d) Be2
5. Identify A in the given chemical reaction.
6. Given below are two statements:
Statement-I: CeO2 can be used for oxidation of aldehydes and ketones.
Statement-II: Aqueous solution of EuSO4 is a strong reducing agent.
(a) Statement I is true, statement II is false
(b) Statement I is false, statement II is true
(c) Both Statement I and Statement II are false
(d) Both Statement I and Statement II are true
7. The major product of the following chemical reaction is:
(a) (CH3CH2CO)2O
(b) CH3CH2CHO
(c) CH3CH2CH3
(d) CH3CH2CH2OH
8. Complete combustion of 1.80 g of an oxygen-containing compound (CxHyOz) gave 2.64 g of CO2 and 1.08 g of H2 The percentage of oxygen in the organic compound is:
(a) 63.53
(b) 51.63
(c) 53.33
(d) 50.33
9. The correct statement about B2H6 is:
(a) All B–H–B angles are of 120°.
(b) Its fragment, BH3, behaves as a Lewis base.
(c) Terminal B–H bonds have less p-character when compared to bridging bonds.
(d) The two B–H–B bonds are not of the same length.
10. In which of the following pairs, the outermost electronic configuration will be the same?
(a) Fe2+ and Co+
(b) Cr+ and Mn2+
(c) Ni2+ and Cu+
(d) V2+ and Cr+
11. Which statement is correct?
(a) Buna-S is a synthetic and linear thermosetting polymer
(b) Neoprene is an addition copolymer used in plastic bucket manufacturing
(c) Synthesis of Buna-S needs nascent oxygen
(d) Buna-N is a natural polymer
12. Given below are two statements:\
Statement-I: An allotrope of oxygen is an important intermediate in the formation of reducing smog.
Statement-II: Gases such as oxides of nitrogen and Sulphur present in the troposphere contribute to the formation of photochemical smog.
(a) Statement I and Statement II are true
(b) Statement I is true about Statement II is false
(c) Both Statement I and Statement II are false
(d) Statement I is false but Statement II is true
13. The plots of radial distribution functions for various orbitals of hydrogen atom against ‘r’ are given below:
(a) (4)
(b) (2)
(c) (1)
(d) (3)
14. Which of the glycosidic linkage galactose and glucose is present in lactose?
(a) C-1 of glucose and C-6 of galactose
(b) C-1 of galactose and C-4 of glucose
(c) C-1 of glucose and C-4 of galactose
(d) C-1 of galactose and C-6 of glucose
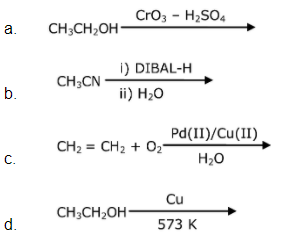
15. Which one of the following reactions will not form acetaldehyde?
16. Which of the following reaction/s will not give p-amino azobenzene?
(a) 2 only
(b) 1 and 2
(c) 3 only
(d) 1 only
17. The hybridization and magnetic nature of [Mn(CN)6]4– and [Fe(CN)6]3–, respectively are:
(a) d2sp3 and paramagnetic
(b) sp3d2 and paramagnetic
(c) d2sp3 and diamagnetic
(d) sp3d2 and diamagnetic
18. Identify A and B in the chemical reaction.
19. Compound(s) which will liberate carbon dioxide with sodium bicarbonate solution is/are:
(a) 2 and 3 only
(b) 1 only
(c) 2 only
(d) 3 only
20. The solubility of AgCN in a buffer solution of pH = 3 is x. The value of x is: [Assume: No cyano complex is formed; Ksp(AgCN) = 2.2 × 10–16 and Ka(HCN) = 6.2 × 10–10]
(a) 0.625 × 10−6
(b) 1.6 × 10−6
(c) 2.2 × 10−6
(d) 1.9 × 10−6
Section-B
21. The reaction of cyanamide, NH2CN(s) with oxygen was run in a bomb calorimeter and ΔU was found to be –742.24 kJ mol–1. The magnitude of ΔH298 for the reaction 
is ______ kJ. (Rounded off to the nearest integer). [Assume ideal gases and R = 8.314 J mol–1 K–1]
22. In basic medium CrO42– oxidizes S2O32– to form SO24 and itself changes into Cr(OH)4–. The volume of 0.154 M CrO42– required to react with 40 mL of 0.25 M S2O32– is ______ mL. (Rounded-off to the nearest integer)
23. For the reaction, aA + bB → cC + dD, the plot of log k vs 1/T is given below:
The temperature at which the rate constant of the reaction is 10–4s–1 is ________ K. [Rounded off to the nearest integer)
[Given: The rate constant of the reaction is 10–5s–1 at 500 K]
24. 0.4g mixture of NaOH, Na2CO3 and some inert impurities was first titrated with N/10HCl using phenolphthalein as an indicator, 17.5 mL of HCl was required at the end point. After this methyl orange was added and titrated. 1.5 mL of the same HCl was required for the next end point. The weight percentage of Na2CO3 in the mixture is ______. (Rounded-off to the nearest integer)
25. The ionization enthalpy of Na+ formation from Na(g) is 495.8 kJ mol–1, while the electron gain enthalpy of Br is –325.0 kJ mol–1. Given the lattice enthalpy of NaBr is –728.4 kJ mol–1. The energy for the formation of NaBr ionic solid is (–)_____ × 10–1 kJ mol–1.
26. Consider the following chemical reaction.
The number of sp2 hybridized carbon atom(s) present in the production is __________.
27. A car tire is filled with nitrogen gas at 35 psi at 27°C. It will burst if pressure exceeds 40 psi. The temperature in °C at which the car tyre will burst is ______. (Rounded-off to the nearest integer)
28. Among the following, the number of halide(s) which is/are inert to hydrolysis is ______.
(a) BF3
(b) SiCl4
(c) PCl5
(d) SF6
29. 1 molal aqueous solution of an electrolyte A2B3 is 60% ionised. The boiling point of the solution at 1 atm is _____ K. (Rounded-off to the nearest integer). [Given Kb for (H2O) = 0.52 K kg mol–1]
30. Using the provided information in the following paper chromatogram:
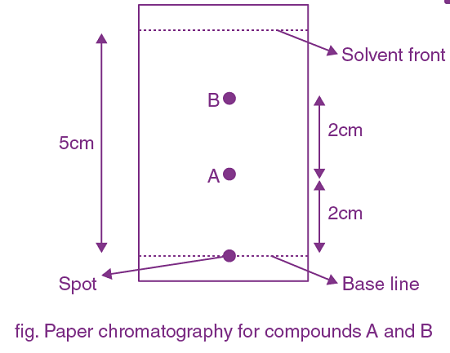
The calculated Rf value of A ______ × 10–1.
Mathematics
Section-A
1. The coefficients a, b and c of the quadratic equation, ax2 + bx + c = 0 are obtained by throwing a dice three times. The probability that this equation has equal roots is :
(a) 1/54
(b) 1/72
(c) 1/36
(d) 5/216
2. Let α be the angle between the lines whose direction cosines satisfy the equations l +m – n = 0 and l2 + m2 – n2 = 0. Then the value of sin4 α + cos4 α is :
(a) 3/4
(b) 1/2
(c) 5/8
(d) 3/8
3. The value of the integral
is
(a) 
(b) 
(c) 
(d) 
4. A man is observing, from the top of a tower, a boat speeding towards the tower from a certain point A, with uniform speed. At that point, the angle of depression of the boat with the man’s eye is 30° (Ignore man’s height). After sailing for 20 seconds towards the base of the tower (which is at the level of water), the boat has reached point B, where the angle of depression is 45°. Then the time taken (in seconds) by the boat from B to reach the base of the tower is :
(a) 10(√3 – 1)
(b) 10√3
(c) 10
(d) 10(√3+1)
5. If 0 < θ, 
, 
and 
then:
(a) xyz = 4
(b) xy – z = (x + y)z
(c) xy + yz + zx = z
(d) xy + z = (x+y)z
6. The equation of the line through the point (0,1,2) and perpendicular to the line 
is:
(a) 
(b) 
(c) 
(d) 
7. The statement A→ (B → A) is equivalent to:
(a) A → (A ᐱ B)
(b) A → (A ᐯ B)
(c) A → (A → B)
(d) A → (A ↔ B)
8. The integer k, for which the inequality x2 – 2(3k – 1)x + 8k2 – 7 > 0 is valid for every x in R is :
(a) 3
(b) 2
(c) 4
(d) 0
9. A tangent is drawn to the parabola y2 = 6x which is perpendicular to the line 2x + y =1. Which of the following points does NOT lie on it?
(a) (0, 3)
(b) (−6, 0)
(c) (4, 5)
(d) (5, 4)
10. Let f, g: N→N such that f(n + 1)= f(n) + f(1) for all n ∈ N and g be any arbitrary function. Which of the following statements is NOT true ?
(a) f is one-one
(b) If fog is one-one, then g is one-one
(c) If g is onto, then fog is one-one
(d) If f is onto, then f(n) = n for all n ∈ Nc
11. Let the lines (2 – i) z = (2 + i) 
and (2 + i)z + (I – 2) − 4i = 0, (here i2 = −1) be normal to a circle C. If the line 
is tangent to this circle C, then its radius is:
(a) 3/√2
(b) 3√2
(c) 3/2√2
(d) 1/2√2
12. All possible values of θ ∈ [0, 2π] for which sin2θ + tan 2θ > 0 lie in
(a) 
(b) 
(c) 
(d) 
13. The image of the point (3,5) in the line x – y + 1 = 0, lies on :
(a) (x – 2)2 + (y – 4) 2 =4
(b) (x – 4)2 + (y + 2) 2 =16
(c) (x – 4)2 + (y – 4) 2 = 8
(d) (x – 2) 2 + (y – 2) 2 =12
14. If Rolle’s theorem holds for the function f(x) = x3 – ax2 + bx – 4, x ∈ [1, 2] with 
then ordered pair (a, b) is equal to :
(a) (–5, 8)
(b) (5, 8)
(c) (5, –8)
(d) (–5, –8)
15. If the curves, 
intersect each other at an angle of 90°, then which of the following relations is true ?
(a) a + b = c + d
(b) a – b = c – d
(c) 
(d) a – c = b + d
16. 
is equal to:
(a) 1/2
(b) 1/e
(c) 1
(d) 0
17. The total number of positive integral solutions (x, y, z) such that xyz = 24 is
(a) 36
(b) 45
(c) 24
(d) 30
18. If a curve passes through the origin and the slope of the tangent to it at any point (x, y) is 
then this curve also passes through the point :
(a) (4, 5)
(b) (5, 4)
(c) (4, 4)
(d) (5, 5)
19. The value of 
where [t] denotes the greatest integer ≤ t, is :
(a) 
(b) 
(c) 
(d) 
20. When a missile is fired from a ship, the probability that it is intercepted is 1/3 and the probability that the missile hits the target, given that it is not intercepted, is 3/4. If three missiles are fired independently from the ship, then the probability that all three hit the target, is:
(a) 1/8
(b) 1/27
(c) 3/4
(d) 3/8
Section-B
21. Let A1, A2, A3, …. be squares such that for each n ≥ 1, the length of the side of An equals the length of diagonal of An+1. If the length of A1 is 12 cm, then the smallest value of n for which area of An is less than one is ____________.
22. The graphs of sine and cosine functions, intersect each other at a number of points and between two consecutive points of intersection, the two graphs enclose the same area A. Then A4 is equal to ___________
23. The locus of the point of intersection of the lines (√3)kx + ky – 4√3 = 0 and √3x – y – 4√3 k = 0 is a conic, whose eccentricity is _________.
24. If 
and 
then 13(a2 + b2) is equal to ________.
25. Let f(x) be a polynomial of degree 6 in x, in which the coefficient of x6 is unity and it has extrema at x = –1 and x = 1. If 
then 5.f(2) is equal to _________.
26. The number of points, at which the function f(x) = |2x + 1| − 3|x + 2| + |x2 + x – 2|, x ∈ R is not differentiable, is ________.
27. If the system of equations
kx + y + 2z = 1
3x – y – 2z = 2
–2x – 2y – 4z = 3
has infinitely many solutions, then k is equal to __________.
28. Let 
and 
be three given vectors. If 
is a vector such that 
then 
is equal to ________
29. Let 
where x, y and z are real numbers such that x + y + z > 0 and xyz = 2.
If A2 = I3, then the value of x3 + y3 + z3 is ________.
30. The total number of numbers, lying between 100 and 1000 that can be formed with the digits 1, 2, 3, 4,5, if the repetition of digits is not allowed and numbers are divisible by either 3 or 5 is ________.
Latest Govt Job & Exam Updates: