Physics
1. A tuning fork A of unknown frequency produces 5 beats/sec with a fork of known frequency 340 Hz. When fork A is filed, the beat frequency decreases to 2 beats/s. What is the frequency of fork A?
(a) 342 Hz
(b) 335 Hz
(c) 338 Hz
(d) 345 Hz
2. The trajectory of a projectile in a vertical plane is y = αx − βx2, where α and β are constants and x and y, are respectively the horizontal and vertical distances of the projectile from the point of projection. The angle of projection θ and the maximum height attained H are respectively given by
(a)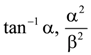 
(b)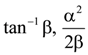 
(c)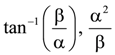 
(d) 
3. A cord is wound around the circumference of a wheel of radius r. The axis of the wheel is horizontal and the moment of inertia about it is I. A weight mg is attached to the cord at the end. The weight falls from rest. After falling through a distance ‘h’, the square of the angular velocity of the wheel will be: (there is no slipping between the wheel and the cord)
(a) 
(b) 2gh
(c) 
(d) 
4. Find the peak current and resonant frequency of the following circuit (as shown in the figure)
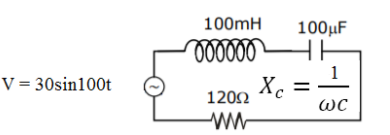
(a) 0.2 A and 100 Hz
(b) 2 A and 50 Hz
(c) 2 A and 100 Hz
(d) 0.2 A and 50 Hz
5. The incident ray, reflected ray and the outward drawn normal are denoted by the unit vectors 
respectively. Then choose the correct relation for these vectors.
(a) 
(b) 
(c) 
(d) 
6. A radioactive sample is undergoing α decay. At any time t1, its activity is A and at another time t2, the activity is A/5. What is the average lifetime for the sample?
(a) 
(b)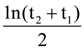 
(c) 
(d) 
7. A particle executes S.H.M., the graph of velocity as a function of displacement is:
(a) a circle
(b) a parabola
(c) an ellipse
(d) a helix
g_collapse]
9. Draw the output Y in the given combination of gates.
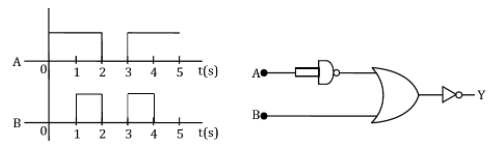
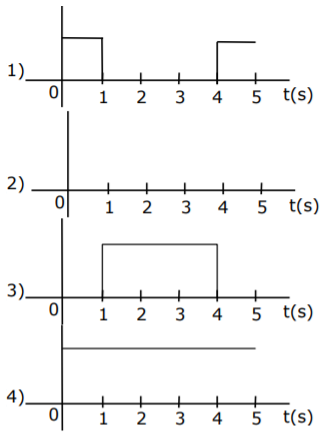
10. An inclined plane making an angle of 300 with the horizontal is placed in a uniform horizontal electric field 
as shown in the figure. A body of mass 1 kg and charge 5 mC is allowed to slide down from rest from a height of 1 m. If the coefficient of friction is 0.2, find the time taken by the body to reach the bottom.
[g = 9.8 m/s2, 
]
(a) 2.3 s
(b) 0.46 s
(c) 1.3 s
(d) 0.92 s
11. If ‘C’ and ‘V’ represent capacitance and voltage respectively then what are the dimensions of λ where C/V = λ?
(a) [M−2L−4I3T7]
(b) [M−2L−3I2T6]
(c) [M−1L−3I−2T−7]
(d) [M−3L−4I3T7]
12. Given below are two statements: One is labelled as Assertion A and the other is labelled as Reason R.
Assertion A: For a simple microscope, the angular size of the object equals the angular size of the image.
Reason R: Magnification is achieved as the small object can be kept much closer to the eye than 25 cm and hence it subtends at a large angle.
In light of the above statements, choose the most appropriate answer from the options given below:
(a) Both A and R are true but R is NOT the correct explanation of A
(b) Both A and R are true and R is the correct explanation of A
(c) A is true but R is false
(d) A is false but R is true
13. The recoil speed of a hydrogen atom after it emits a photon in going from n = 5 state to n = 1 state will be:
(a) 4.17 m/s
(b) 4.34 m/s
(c) 219 m/s
(d) 3.25 m/s
14. Two masses A and B, each of mass M are fixed together by a massless spring. A force acts on mass B as shown in the figure. If mass A starts moving away from mass B with acceleration ‘a’, then the acceleration of mass B will be:
(a) 
(b) 
(c) 
(d) 
15. A wire of 1Ω has a length of 1 m. It is stretched till its length increases by 25%. The percentage change in resistance to the nearest integer is:
(a) 25%
(b) 12.5%
(c) 76%
(d) 56%
16. Given below are two statements:
Statement (1):- A second’s pendulum has a time period of 1 second.
Statement (2):- It takes precisely one second to move between the two extreme positions.
In light of the above statements, choose the correct answer from the options given below.
(a) Both Statement I and Statement II are false
(b) Statement I is true but Statement II is false
(c) Statement I is false but Statement II is true
(d) Both Statement I and Statement II is true
17. An aeroplane with its wings, spread 10 m, is flying at a speed of 180 km/h in a horizontal direction. The total intensity of the magnetic field at that part is 2.5 × 10–4 Wb/m2 and the angle of dip is 60°. The emf induced between the tips of the plane wings will be:
(a) 88.37 mV
(b) 62.50 mV
(c) 54.125 mV
(d) 108.25 mV
18. The length of the metallic wire is l1 when the tension in it is T1. It is l2 when the tension is T2. The original length of the wire will be:
(a) 
(b) 
(c) 
(d) 
19. The internal energy (U), pressure (P) and volume (V) of an ideal gas are related as U = 3PV + 4. The gas is:
(a) polyatomic only
(b) monoatomic only
(c) either monoatomic or diatomic
(d) diatomic only.
20. Given below are two statements:
Statement – I: An electric dipole is placed at the centre of a hollow sphere. The flux of the electric field through the sphere is zero but the electric field is not zero anywhere in the sphere.
Statement – II: If R is the radius of a solid metallic sphere and Q be the total charge on it. The electric field at any point on the spherical surface of radius r (< R) is zero but the electric flux passing through this closed spherical surface of radius r is not zero.
In the light of the above statements Choose the correct answer from the option given below:
(a) Statement I is true but Statement II is false
(b) Statement I is false but Statement II is true
(c) Both Statement I and Statement II are true
(d) Both Statement I and Statement II are false
Section-B
21. If the highest frequency modulating a carrier is 5 kHz, then the number of AM broadcast stations accommodated in a 90 kHz bandwidth are ___________.
22. 1 mole of a rigid diatomic gas performs a work of Q/5. when heat Q is supplied to it. The molar heat capacity of the gas during this transformation is xR/8. The value of x is _________.
23. A particle executes S.H.M with amplitude ‘a’ and time period T. The displacement of the particle from the mean position when its speed is half of the maximum speed is √xa/2. The value of x is ________
24. Two stream of photons, possessing energies equal to twice and ten times the work function of metal are incident on the metal surface successively. The value of the ratio of maximum velocities of the photoelectrons emitted in the two respective cases is x : 3. The value of x is ________.
25. A point source of light S, placed at a distance 60 cm in front of the centre of the plane mirror of width 50 cm, hangs vertically on a wall. A man walks in front of the mirror along a line parallel to the mirror at a distance 1.2 m from it (see in the figure). The distance between the extreme points where he can see the image of the light source in the mirror is ________cm
26. The Zener diode has a VZ = 30 V. The current passing through the diode for the following circuit is ______ mA.
27. In the reported figure of the earth, the value of acceleration due to gravity is the same at point A and C but it is smaller than that of its value at point B (surface of the earth). The value of OA : AB will be x : 5. The value of x is ____________.
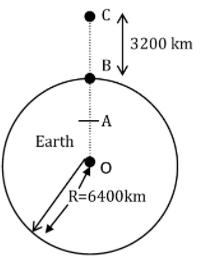
28. 27 similar drops of mercury are maintained at 10 V each. All these spherical drops combine into a single big drop. The potential energy of the bigger drop is _____ times that of a smaller drop.
29. The volume V of a given mass of monatomic gas changes with temperature T according to the relation V = KT2/3. The work done when temperature changes by 90 K will be xR. The value of x is ____. [R = universal gas constant]
30. Time period of a simple pendulum is T. The time taken to complete 5/8 oscillations starting from mean position is 
The value of α is ___________.
Chemistry
Section-A
1. 2,4-DNP test can be used to identify
(a) aldehyde
(b) halogens
(c) ether
(d) amine
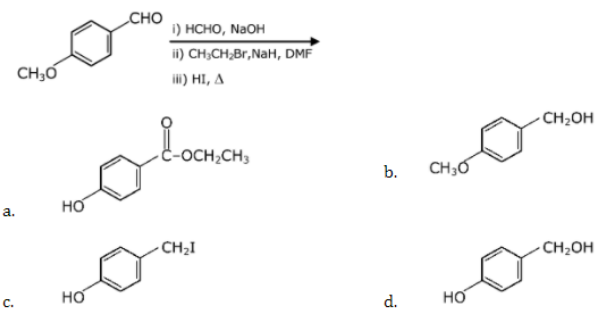
2. Identify A in the following chemical reaction.
3. The nature of charge on resulting colloidal particles when FeCl3 is added to excess of hot water is:
(a) positive
(b) neutral
(c) sometimes positive and sometimes negative
(d) negative
4. Match List-I with List-II
Choose the correct answer from the option given below:
(a) (a)-(ii), (b)-(i), (c)-(iv), (d)-(iii)
(b) (a)-(iii), (b)-(iv), (c)-(i), (d)-(ii)
(c) (a)-(ii), (b)-(iv), (c)-(i), (d)-(iii)
(d) (a)-(iii), (b)-(i), (c)-(iv), (d)-(ii)
5. In 
molecule, the hybridization of carbon 1, 2, 3 and 4 respectively are:
(a) sp2, sp, sp2, sp3
(b) sp2, sp2, sp2, sp3
(c) sp2, sp3, sp2, sp3
(d) sp3, sp, sp3, sp3
6. Match List-I with List-II.
List-I List-II
(a) Sucrose (i) b-D-Galactose and b-D-Glucose
(b) Lactose (ii) a-D-Glucose and b-D-Fructose
(c) Maltose (iii) a-d-Glucose and a-D-Glucose
Choose the correct answer from the options given below:
(a) (a)-(iii), (b)-(ii), (c)-(i)
(b) (a)-(iii), (b)-(i), (c)-(ii)
(c) (a)-(i), (b)-(iii), (c)-(ii)
(d) (a)-(ii), (b)-(i), (c)-(iii)
7. Which pair of oxides is acidic in nature?
(a) N2O, BaO
(b) CaO, SiO2
(c) B2O3, CaO
(d) B2O3, SiO2
8. Calgon is used for water treatment. Which of the following statements is NOT true about Calgon?
(a) Calgon contains the 2nd most abundant element by weight in the earth’s crust
(b) It is also known as Graham’s salt.
(c) It is a polymeric compound and is water-soluble.
(d) It does not remove Ca2+ ion by precipitation.
9. Ceric ammonium nitrate and CHCl3/alc. KOH are used for the identification of functional groups present in _________and________ respectively.
(a) alcohol, amine
(b) amine, alcohol
(c) alcohol, phenol
(d) amine, phenol
10. Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R.
Assertion A: In TlI3, isomorphous to CsI3, the metal is present in +1 oxidation
state.
Reason R: Tl metals has fourteen f electrons in its electronic configuration.
In the light of the above statements, choose the most appropriate Answer from the options given below:
(a) Both A and R are correct and R is the correct explanation of A
(b) A is not correct but R is correct
(c) Both A and R are correct R is NOT the correct explanation of A
(d) A is correct but R is not correct
11. Thallium shows Tl+ state due to inert pair effect. The correct order of electron gain enthalpy is
(a) S > Se > Te > O
(b) O > S > Se > Te
(c) S > O > Se > Te
(d) Te > Se > S > O
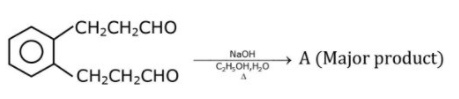
12. Identify A in the given chemical reaction.
13. Match List-I with List-II
List-I List-II
(a) Siderite (i) Cu
(b) Calamine (ii) Ca
(c) Malachite (iii) Fe
(d) Cryolite (iv) Al
(v) Zn
Choose the correct answer from the options given below:
(a) (a)-(i), (b)-(ii), (c)-(v), (d)-(iii)
(b) (a)-(iii), (b)-(v), (c)-(i), (d)-(iv)
(c) (a)-(i), (b)-(ii), (c)-(iii), (d)-(iv)
(d) (a)-(iii), (b)-(i), (c)-(v), (d)
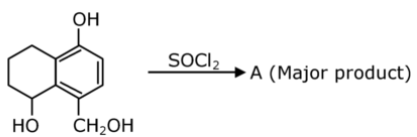
14. Identify A in the given reaction.
15. Match List-I with List-II
List-I List-II
(a) Sodium Carbonate (i) Deacon
(b) Titanium (ii) Caster-Kellner
(c) Chlorine (iii) Van-Arkel
(d) Sodium hydroxide (iv) Solvay
Choose the correct answer from the option given below
(a) (a)-(iii), (b)-(ii), (c)-(i), (d)-(iv)
(b) (a)-(iv), (b)-(iii), (c)-(i), (d)-(ii)
(c) (a)-(iv), (b)-(i), (c)-(ii), (d)-(iii)
(d) (a)-(i), (b)-(iii), (c)-(iv), (d)-(ii)
16. Match List-I with List-II.
List-I List-II
Molecule (Bond order)
(a) Ne2 (i) 1
(b) N2 (ii) 2
(c) F2 (iii) 0
(d) O2 (iv) 3
Choose the correct answer from the options given below:
(a) (a)-(iii), (b)-(iv), (c)-(i), (d)-(ii)
(b) (a)-(i), (b)-(ii), (c)-(iii), (d)-(iv)
(c) (a)-(ii), (b)-(i), (c)-(iv), (d)-(iii)
(d) (a)-(iv), (b)-(iii), (c)-(ii), (d)-(i)
17. Which of the following forms of hydrogen emits low energy b- particles?
(a) Proton H+
(b) 
(c) 
(d) 
18. Choose the correct order of the basic nature of the below given amines.
(A) Phenyl methanamine
(B) N, N-Dimethylaniline
(C) N-Methyl aniline
(D) Benzenamine
(a) D > C > B > A
(b) D > B > C > A
(c) A > C > B > D
(d) A > B > C > D
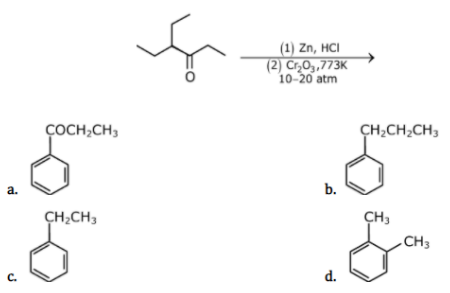
19. Considering the given reaction, the major product among the following is:
20. Seliwanoff test and Xanthoproteic test are used for the identification of __________ and ___________ respectively
(a) ketoses, proteins
(b) proteins, ketoses
(c) aldoses, ketoses
(d) ketoses, aldoses
Section-B
21. The NaNO3 weighed out to make 50 mL of an aqueous solution containing 70.0 mg Na+ per mL is ________g. (Rounded off to the nearest integer)
[Given: Atomic weight in g mol–1. Na: 23; N: 14; O: 16.
22. The number of stereoisomers possible for [Co(ox)2(Br)(NH3)]2− is ____________. [ox = oxalate]
23. The average S–F bond energy in kJ mol–1 of SF6 is __________. (Rounded off to the nearest integer)
[Given : The values of standard enthalpy of formation of SF6(g), S(g) and F(g) are – 1100, 275 and 80 kJ mol–1 respectively.]
24. e.m.f of the following cell at 298 K in V is x ×10−2.
Zn|Zn2+ (0.1 M)||Ag+(0.01 M)| Ag
The value of x is _________. (Rounded off to the nearest integer)
25. A ball weighing 10g is moving with a velocity of 90ms−1. If the uncertainty in its velocity is 5%, then the uncertainty in its position is ________×10−33 (Rounded off to the nearest integer)
[Given: h = 6.63×10−34 J s]
26. In a mildly alkaline medium, thiosulphate ion is oxidized by to “A”. The oxidation state of sulphur in “A” is ________.
27. When 12.2 g of benzoic acid is dissolved in 100g of water, the freezing point of solution was found to be –0.93°C (Kf (H2O) = 1.86 K kg mol−1). Then the number (n) of benzoic acid molecules associated (assuming 100% association) is_____________.
28. If the activation energy of a reaction is 80.9 kJ mol–1, the fraction of molecules at 700K, having enough energy to react to form products is e–x. The value of x is ______. (Rounded off to the nearest integer)
[Use R = 8.31 JK−1 mol−1]
29. The pH of ammonium phosphate solution, if pka of phosphoric acid and pkb of ammonium hydroxide are 5.23 and 4.75 respectively, is_____________.
30. The number of octahedral voids per lattice site in a lattice is __________.
(Rounded off to the nearest integer)
Mathematics
Section-A
1. Let L be a line obtained from the intersection of two planes x + 2y + z = 6 and y + 2z = 4. If point P (ɑ, β, γ) is the foot of the perpendicular from (3, 2, 1) on L, then the value of 21 (ɑ + β + γ) equals:
(a) 142
(b) 68
(c) 136
(d) 102
2. The sum of the series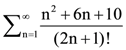
is equal to:
(a)
(b) 
(c) 
(d) 
3. Let f(x) be a differentiable function at x = a with f’ (a) = 2 and f (a) = 4. Then 
equals:
(a) 2a + 4
(b) 2a – 4
(c) 4 – 2a
(d) a + 4
4. Let A (1, 4) and B (1, −5) be two points. Let P be a point on the circle (x − 1)2 + (y − 1)2 = 1 such that (PA)2 + (PB)2 have maximum value, then the points P, A and B lie on:
(a) a parabola
(b) a straight line
(c) a hyperbola
(d) an ellipse
5. If the locus of the mid-point of the line segment from the point (3, 2) to a point on the circle, x2 + y2 = 1 is a circle of the radius r, then r is equal to :
(a) 14
(b) 12
(c) 1
(d) 13
6. Let the slope of the tangent line to a curve at any point P (x, y) be given by 
If the curve intersects the line x + 2y = 4 at x = −2, then the value of y, for which the point (3, y) lies on the curve, is:
(a) −18/11
(b) −18/19
(c) −4/3
(d) 18/35
7. Let A1 be the area of the region bounded by the curves y = sinx, y = cos x and y-axis in the first quadrant. Also, let A2 be the area of the region bounded by the curves y = sinx, y = cosx, the x-axis and x = π/2 in the first quadrant. Then,
(a) A1 = A2 and A1 + A2 = √2
(b) A1 : A2 = 1 : 2 and A1 + A2 = 1
(c) 2A1 = A2 and A1 + A2 = 1 + √2
(d) A1 : A2 = 1 : √2 and A1 + A2 = 1
8. If 0 < a, b < 1, and tan−1 a + tan−1 b = π/4, then the value of 
is :
(a) loge 2
(b) loge (e/2)
(c) e
(d) e2 – 1
9. Let F1 (A, B, C) = (A ∧ ~B) ∨ [~C ∧ (A ∨ B)] ∨ ~A and F2 (A, B) = (A ∨ B) ∨ (B → ~A) be two logical expressions. Then:
(a) F1 is not a tautology but F2 is a tautology
(b) F1 is a tautology but F2 is not a tautology
(c) F1 and F2 both area tautologies
(d) Both F1 and F2 are not tautologies
10. Consider the following system of equations:
x + 2y − 3z = a
2x + 6y − 11 z = b
x − 2y + 7z = c,
Where a, b and c are real constants. Then the system of equations:
(a) has a unique solution when 5a = 2b + c
(b) has an infinite number of solutions when 5a = 2b + c
(c) has no solution for all a, b and c
(d) has a unique solution for all a, b and c
11. A seven-digit number is formed using the digit 3, 3, 4, 4, 4, 5, 5. The probability, that number so formed is divisible by 2, is:
(a) 6/7
(b) 4/7
(c) 3/7
(d) 1/7
12. If
vectors are collinear, then a possible unit vector parallel to the vector 
is:
(a)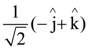 
(b)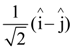 
(c)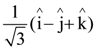 
(d)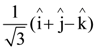 
13. For x > 0, if 
is equal to:
(a) 1/2
(b) −1
(c) 1
(d) 0
14. Let f : R → R be defined as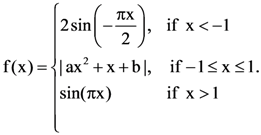 
If f(x) is continuous on R, then a + b equals:
(a) 3
(b) −1
(c) −3
(d) 1
15. Let A = {1, 2, 3 ……. , 10} and f : A → A be defined as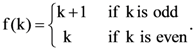 
Then the number of possible functions g : A → A such that gof = f is:
(a) 105
(b) 10C5
(c) 55
(d) 5!
16. A natural number has prime factorization given by n = 2x3y5z, where y and z are such that y + z = 5 and y−1 + z−1 = 5/6, y > z. Then the number of odd divisors of n, including 1, is:
(a) 11
(b) 6x
(c) 12
(d) 6
17. Let f(x) = sin−1 x and 
If 
then the domain of the function fog is:
(a) (−∞, −2] ⋃ [−4/3, ∞]
(b) (−∞,−1] ⋃ [2, ∞)
(c) (−∞, −2] ⋃ [−1, ∞]
(d) (−∞, 2] ⋃ [−3/2, ∞)
18. If the mirror image of the point (1, 3, 5) with respect to the plane 4x – 5y + 2z = 8 is (ɑ, β, γ), then 5 (ɑ + β + γ) equals:
(a) 47
(b) 39
(c) 43
(d) 41
19. Let 
be a differentiable function for all x ∈ then f(x) equals.
(a) 
(b) 
(c) 
(d) 
20. The triangle of the maximum area that can be inscribed in a given circle of radius ‘r’ is:
(a) A right-angle triangle having two of its sides of length 2r and r.
(b) An equilateral triangle of height 2r/3.
(c) isosceles triangle with base equal to 2r.
(d) An equilateral triangle having each of its side of length √3r.
Section-B
21. The total number of 4-digit numbers whose greatest common divisor with 18 is 3, is _______
22. Let ɑ and β be two real numbers such that ɑ + β = 1 and ɑ β = − Let Pn = (ɑ)n + (β)n, Pn – 1 = 11 and Pn+1 = 29 for some integer n ≥ 1. Then, the value of Pn2 is__________.
23. Let X1, X2, …. X18 be eighteen observation such that 
where ɑ and β are distinct real numbers. If the standard deviation of these observations is 1, then the value of |ɑ − β| is ___________.
24. In 
for m, n ≥ 1 and 
then α equals ______
25. Let L be a common tangent line to the curves 4x2 + 9y2 = 36 and (2x)2 + (2y)2 = 31. Then the square of the slope of the line L is __________.
26. If the matrix 
satisfies the equation 
for some real numbers α and β, then β – α is equal to_______.
27. If the arithmetic mean and the geometric mean of the pth and qth terms of the sequence −16, 8, −4, 2, … satisfy the equation 4x2 − 9x + 5 = 0, then p + q is equal to ______________.
28. Let the normals at all the points on a given curve pass through a fixed point (a, b). If the curve passes through (3, −3) and (4, −2 √2), and given that a − 2√2b = 3, then (a2 + b2 + ab) is equal to______________.
29. Let z be those complex number which satisfies |z + 5| ≤ 4 and 
If the maximum value of |z + 1|2 is ɑ + β√2, then the value of ɑ + β is ________.
30. Let a be an integer such that all the real roots of the polynomial 2x5 + 5x4 + 10x3 + 10x2 + 10x + 10 lie in the interval (a, a + 1). Then, |a| is equal to _______.
Latest Govt Job & Exam Updates: