Physics
Section-A
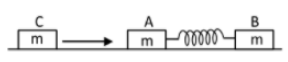
1. Two identical blocks A and B each of mass m resting on the smooth horizontal floor are connected by a light spring of natural length L and spring constant K. A third block C of mass m moving with a speed v along the line joining A and B collides elastically with A. The maximum compression in the spring is
(a) 
(b) 
(c) 
(d) 
2. A solid sphere of mass 2 kg radius 0.5m is rolling with an initial speed of 1 ms−1 goes up an inclined plane which makes an angle of 300 with the horizontal plane, without slipping. How long will the sphere take to return to the starting point A?
(a) 0.80 s
(b) 0.60 s
(c) 0.52 s
(d) 0.57 s
3. If one mole of a polyatomic gas has two vibrational modes and β is the ratio of molar specific heats for polyatomic gas β=Cp/ Cv then the value of β is :
(a) 1.35
(b) 1.02
(c) 1.25
(d) 1.2
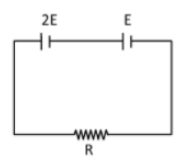
4. Two cells of emf 2E and E with internal resistance r1 and r2 respectively are connected in series to an external resistor R (see figure). The value of R, at which the potential difference across the terminals of the first cell becomes zero is
(a) r1 – r2
(b) r1 + r2
(c) 
(d) 
5. A sound wave of frequency 245 Hz travels with a speed of 300 ms−1 along the positive x-axis. Each point of the medium moves to and fro through a total distance of 6 cm. What will be the mathematical expression of the travelling wave?
(a) Y (x, t) = 0.03 [ sin 5.1x − (0.2 x 103)t]
(b) Y (x, t) = 0.06 [ sin 5.1x − (1.5 x 103)t]
(c) Y (x, t) = 0.06 [ sin 0.8x − (0.5 x 103)t]
(d) Y (x, t) = 0.03 [ sin 5.1x − (1.5 x 103)t]
6. A carrier signal C(t) = 25 sin (2.512 × 1010t) is amplitude modulated by a message signal m(t)= 5 sin (1.57 × 108t) and transmitted through an antenna. What will be the bandwidth of the modulated signal?
(a) 1987.5 MHz
(b) 2.01 GHz
(c) 50 MHz
(d) 8 GHz
7. Two particles A and B of equal masses are suspended from two massless springs of spring constants K1 and K2 If the maximum velocities during oscillations are equal, the ratio of the amplitude of A and B is :
(a) 
(b) 
(c) 
(d) 
8. Match List I with List II
| List I | List II |
| (a) Phase difference between current and voltage in a purely resistive AC circuit | (i) 𝜋/2, current leads voltage |
| (b) Phase difference between current and voltage in a pure inductive AC circuit | (ii) zero |
| (c) Phase difference between current and voltage in a pure capacitive AC circuit | (iii) 𝜋/2, current lags voltage |
| (d) Phase difference between current and voltage in an LCR series circuit | (iv)  |
Choose the most appropriate answer from the options given below :
(a) (a)-(ii), (b)-(iii), (c)-(iv), (d)-(i)
(b) (a)-(i), (b)-(iii), (c)-(iv), (d)-(ii)
(c) (a)-(ii), (b)-(iv), (c)-(iii), (d)-(i)
(d) (a)-(ii), (b)-(iii), (c)-(i), (d)-(iv)
9. A geostationary satellite is orbiting around an arbitrary planet ‘P’ at a height of 11R above the surface of ‘P’, R being the radius of ‘P’. The time period of another satellite in hours at a height of 2R from the surface of ‘P’ is _____. ‘P’ has a time period of rotation of 24 hours.
(a) 6/√2
(b) 3
(c) 6√2
(d) 5
10. The velocity of a particle is v=v0 + gt + Ft2. Its position is x = 0 at t = 0; then its displacement after time (t = 1) is :
(a) 
(b) v0 + 2g + 3f
(c) v0 + g + F
(d) 
11. A block of mass 1 kg attached to a spring is made to oscillate with an initial amplitude of 12 cm. After 2 minutes the amplitude decreases to 6 cm. Determine the value of the damping constant for this motion. (take ln 2 = 0.693).
(a) 3.3 × 102 kg s−1
(b) 5.7 × 10−3 kg s−1
(c) 1.16 × 10−2 kg s−1
(d) 0.69 × 102 kg s−1
12. An object is located 2 km beneath the surface of the water. If the fractional compression ∆V/V is 1.36%, the ratio of hydraulic stress to the corresponding hydraulic strain will be ……..
[Given: density of water is 1000 kgm–3 and g= 9.8 ms–2]
(a) 2.26 ×109 Nm−2
(b) 1.96 ×109 Nm−2
(c) 1.44 ×107 Nm−2
(d) 1.44 ×109 Nm−2
13. Two identical photocathodes receive the light of frequencies f1 and f2 If the velocities of the photo-electrons coming out are v1 and v2 respectively, then
(a)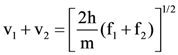 
(b) 
(c) 
(d) 
14. The atomic hydrogen emits a line spectrum consisting of various series. Which series of hydrogen atomic spectra lie in the visible region?
(a) Balmer series
(b) Lyman series
(c) Brackett series
(d) Paschen series
15. Which one of the following will be the output of the given circuit?
(a) NAND Gate
(b) AND Gate
(c) XOR Gate
(d) NOR Gate
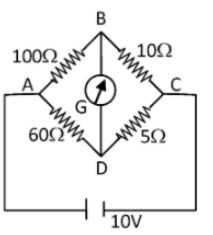
16. The four arms of a Wheatstone bridge have resistances as shown in the figure. A galvanometer of 15 resistance is connected across BD. Calculate the current through the galvanometer when a potential difference of 10 V is maintained across AC.
(a) 4.87 mA
(b) 4.87 μA
(c) 2.44 μA
(d) 2.44 mA
17. Which one is the correct option depicting the two different thermodynamic processes?
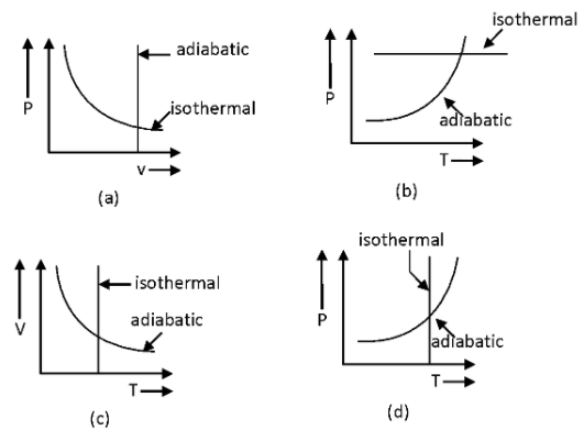
(a) (c) and (d)
(b) (b) and (c)
(c) (a) only
(d) (c) and (a)
18. A hairpin-like shape as shown in the figure is made by bending a long current-carrying wire. What is the magnitude of a magnetic field at point P which lies on the centre of the semicircle?
(a) 
(b) 
(c) 
(d) 
19. A rubber ball is released from a height of 5 m above the floor. It bounces back repeatedly, always rising to (81/100) of the height through which it falls. Find the average speed of the ball. (Take g=10 ms−2)
(a) 2.50 ms−1
(b) 3.50 ms−1
(c) 3.0 ms−1
(d) 2.0 ms−1
20. What happens to the inductive reactance and the current in a purely inductive circuit if the frequency is halved?
(a) Both, including reactance and current, will be doubled
(b) Both, inductive reactance and current will be halved
(c) Inductive reactance will be halved and current will be doubled
(d) Inductive reactance will be doubled and current will be halved
Section-B
21. The electric field intensity produced by the radiation coming from a 100 W bulb at a distance of 3 m is E. The electric field intensity produced by the radiation coming from 60 W at the same distance is 
Where the value of x = ________
22. The image of an object placed in the air formed by a convex refracting surface is at a distance of 10 m behind the surface. The image is real and is at 2nd/3 of the distance of the object from the surface. The wavelength of light inside the surface is 2/3 times the wavelength in air, The radius of the curved surface is x/13 m. The value of ‘x’ is _____
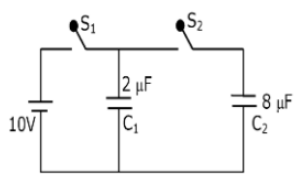
23. A 2μF capacitor C1 is first charged to a potential difference of 10V using a battery. Then the battery is removed and the capacitor is connected to an uncharged capacitor C2 of 8 μF. The charge in C2 on equilibrium condition is ________ μC. (Round off to the Nearest Integer)
24. A particle of mass m moves in a circular orbit in a central potential field U(r) =U0r4. If Bohr’s quantization conditions are applied, radii of possible orbital rn vary with n1/α, where α is _____
25. The electric field in a region is given by 
with 
The flux of this field through a rectangular surface are 0.4 m2 parallel to Y-Z plane is _______Nm2C−1.
26. A body of mass 1 kg rests on a horizontal floor with which it has a coefficient of static friction 1/√3. It is desired to make the body move by applying the minimum possible force F N. The value of F will be __________. (Round off to the Nearest Integer)
[Take g = 10 ms−2]
27. Seawater at a frequency f = 9 × 102 Hz, has permittivity ∈ = 80∈0 and resistivity ρ = 0.25 Ωm. Imagine a parallel plate capacitor is immersed in seawater and is driven by an alternating voltage source V(t) = V0 sin(2πft). Then the conduction current density becomes 10x times the displacement current density after time t= 1800. The value of x is __________.
(Given :
)
28. The disc of mass M with uniform surface mass density σ is shown in the figure. The centre of mass of the quarter disc (the shaded area) is at the position 
x is _____(Round off to the Nearest Integer) [a is an area as shown in the figure)
29. Suppose you have taken a dilute solution of oleic acid in such a way that its concentration becomes 0.01 cm3 of oleic acid per cm3 of the solution. Then you make a thin film of this solution (monomolecular thickness) of area 4 cm2 by considering 100 spherical drops of radius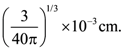 
Then the thickness of the oleic acid layer will be x × 10−14 m where x is _________.
30. A boy of mass 4 kg is standing on a piece of wood having mass 5 kg. If the coefficient of friction between the wood and the floor is 0.5, the maximum force that the boy can exert on the rope so that the piece of wood does not move from its place is ________N. (Round off to the Nearest Integer)
[Take g = 10 ms−2]
Chemistry
Section-A
1. Match List-I with List-II.
List-I List-II
Chemical Compound Used as
(a) Sucralose (i) Synthetic detergent
(b) Glyceryl ester of stearic acid (ii) Artificial sweetener
(c) Sodium benzoate (iii) Antiseptic
(d) Bithionol (iv) Food preservative
Choose the correct match:
(a) (a)-(i), (b)-(ii), (c)-(iv), (d)-(iii)
(b) (a)-(ii), (b)-(i), (c)-(iv), (d)-(iii)
(c) (a)-(iv), (b)-(iii), (c)-(ii), (d)-(i)
(d) (a)-(iii), (b)-(ii), (c)-(iv), (d)-(i)
2. In the below reactions, enzyme A and enzyme B respectively are:
(a) Invertase and Amylase
(b) Amylase and Invertase
(c) Invertase and Zymase
(d) Zymase and Invertase
3. The correct pair(s) of the ambident nucleophiles is (are):
(A) AgCN/KCN
(B) RCOOAg/RCOOK
(C) AgNO2/KNO2
(D) AgI/KI
(a) (A) and (C) only
(b) (B) only
(c) (B) and (C) only
(d) (A) only
4. During which of the following processes, does entropy decrease?
(A) Freezing of water to ice at 0°C
(B) Freezing of water to ice at -10°C
(C) N2(g) + 3H2(g) →2NH3(g)
(D) Adsorption of CO(g) on lead surface.
(E) Dissolution of NaCI in water
(a) (A), (B), (C) and (D) only
(b) (A), (C) and (E) only
(c) (A) and (E) only
(d) (B) and (C) only
5. Match List-I with List-II:
List – I List – II
(a) [Co(NH3)6] [Cr(CN)6] (i) Linkage isomerism
(b) [Co(NH3)3 (NO2)3] (ii) Solvate isomerism
(c) [Cr(H2O)6]Cl3 (iii) Coordination isomerism
(d) cis-[CrCl2(ox)2]3− (iv) Optical isomerism
Choose the correct answer from the options given below:
(a) (a)-(iii), (b)-(i), (c)-(ii), (d)-(iv)
(b) (a)-(i), (b)-(ii), (c)-(iii), (d)-(iv)
(c) (a)-(ii), (b)-(i), (c)-(iii), (d)-(iv)
(d) (a)-(iv), (b)-(ii), (c)-(iii), (d)-(i)
6. The common positive oxidation states for an element with atomic number 24, are
(a) +1 and +3
(b) +1 to +6
(c) +1 and +3 to +6
(d) +2 to +6
7. The set of elements that differ in a mutual relationship from those of the other sets is:
(a) Be – Al
(b) Li – Na
(c) B – Si
(d) Li – Mg
8. Given below are two statements:
Statement I: 2-methyl butane on oxidation with KMnO4 gives 2-methyl butane-2-ol.
Statement II: n-alkanes can be easily oxidized to corresponding alcohols with KMnO4.
Choose the correct option:
(a) Both statement I and statement II are incorrect
(b) Statement I is correct but statement II is incorrect
(c) Both statement I and statement II are correct
(d) Statement I is incorrect but statement II is correct
9. Amongst the following, the linear species is:
(a) N3−
(b) Cl2O
(c) O3
(d) NO2
10. For the coagulation of a negative sol, the species below, that has the highest flocculating power is:
(a) SO42−
(b) Na+
(c) Ba2+
(d) PO43
11. The functional groups that are responsible for the ion-exchange property of cation and anion exchange resins, respectively, are:
(a) –SO3H and –COOH
(b) –SO3H and –NH2
(c) –NH2 and –SO3H
(d) –NH2 and –COOH
12. Choose the correct statement regarding the formation of carbocations A and B given.
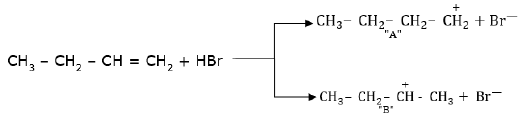
(a) Carbocation A is more stable and formed relatively at a faster rate
(b) Carbocation B is more stable and formed relatively at a faster rate
(c) Carbocation A is more stable and formed relatively at a slow rate
(d) Carbocation B is more stable and formed relatively at a slow rate
13. In the below reaction, the structural formula of (A), “X” and “Y” respectively are:
14. Fructose is an example of:
(a) Heptose
(b) Aldohexose
(c) Pyranose
(d) Ketohexose
15. Which of the following statement(s) is (are) the incorrect reason for eutrophication?
(A) excess usage of fertilisers
(B) excess usage of detergents
(C) dense plant population in water bodies
(D) lack of nutrients in water bodies that prevent plant growth
Choose the most appropriate answer from the option given below:
(a) (D) only
(b) (C) only
(c) (B) and (D) only
(d) (A) only
16. Primary, secondary and tertiary amines can be separated using:
(a) Para-Toluene sulphonyl chloride
(b) Chloroform and KOH
(c) Acetyl amide
(d) Benzene sulphonic acid
17. Match List-I with List-II
List-I List-II
(a) Haematite (i) Al2O3. xH2O
(b) Bauxite (ii) Fe2O3
(c) Magnetite (iii) CuCO3. Cu(OH)2
(d) Malachite (iv) Fe3O4
Choose the correct answer from the options given below:
(a) (a)-(ii), (b)-(iii), (c)-(i), (d)-(iv)
(b) (a)-(iv), (b)-(i), (c)-(ii), (d)-(iii)
(c) (a)-(i), (b)-(iii), (c)-(ii), (d)-(iv)
(d) (a)-(ii), (b)-(i), (c)-(iv), (d)-(iii)
18. The set that represents the pair of neutral oxides of nitrogen is:
(a) NO and N2O
(b) NO and NO2
(c) N2O and NO2
(d) N2O and N2O3
19. Nitrogen can be estimated by Kjeldahl’s method for which of the following compound?
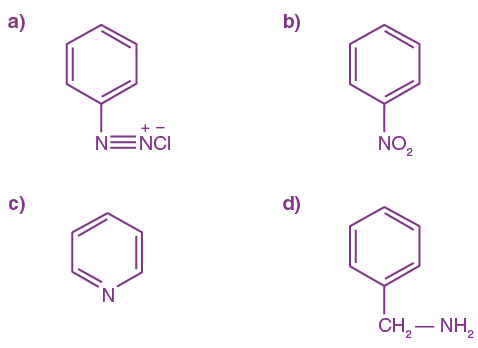
20. One of the by-products formed during the recovery of NH3 from Solvay process is:
(a) NaHCO3
(b) Ca(OH)2
(c) CaCl2
(d) NH4Cl
SECTION – B
21. The reaction 2A + B2→ 2AB is an elementary reaction. For a certain quantity of reactants, if the volume of the reaction vessel is reduced by a factor of 3, the rate of the reaction increases by a factor of ……………. (Round off to the Nearest Integer).
22. In the ground state of atomic Fe (Z = 26), the spin-only magnetic moment is ……………..x 10−1 (Round off to the Nearest Integer).
[Given: √3 = 1.73, √2 = 1.41]
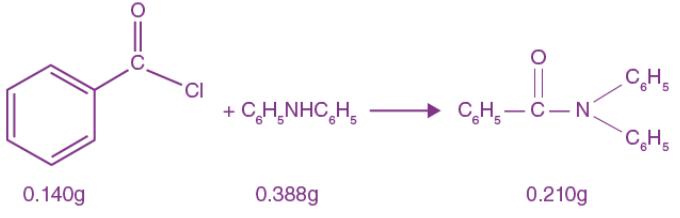
23. Consider the below-given reaction. The percentage yield of an amide product is ………………. (Round off to the Nearest Integer). [Given: Atomic mass: C: 12.0 u, H : 1.0 u, N : 14.0, O : 16.0 u, Cl : 35.5 u]
24. On complete reaction of FeCl3 with oxalic acid in an aqueous solution containing KOH, resulted in the formation of product A. The secondary valency of Fe in the product A is …………..(Round off to the Nearest Integer)
25. Consider the reaction N2O4 (g) ⇌ 2NO2 (g). The temperature at which KC = 20.4 and KP = 600.1, is …………………. K. (Round off to the Nearest Integer). [Assume all gases are ideal and R = 0.0831 L bar K−1 mol−1]
26. A KCl solution of conductivity 0.14 S m-1 shows a resistance of 4.19 Ω in a conductivity cell. If the same cell is filled with an HCl solution, the resistance drops 1.03 Ω. The conductivity of the HCl solution is ……………….. × 10−2 S m−1. (Round off to the Nearest Integer).
27. A 1 molal K4Fe(CN)6 solution has a degree of dissociation of 0.4. Its boiling point is equal to that of another solution which contains 18.1 weight per cent of a nonelectrolyte solute A. The molar mass of A is …………… g/mol. (Round off to the Nearest Integer).
28. The number of chlorine atoms in 20 mL of chlorine gas at STP is ………1021. (Round off to the Nearest Integer).
[Assume chlorine is an ideal gas at STP
R=0.083 L bar mol−1 K−1, NA = 6.023 × 1023]
29. KBr is doped with 10−5 mole per cent of SrBr2. The number of cationic vacancies in 1 g of KBr crystal is ……… 1014. (Round off to the Nearest Integer).
[Atomic Mass: K = 39.1 u, Br = 79.9 u, NA = 6.023 × 1023]
30 The total number of C–C sigma bond/s in mesityl oxide (C6H10O) is …… (Round off to the Nearest Integer).
Mathematics
Section-A
1. If the Boolean expression (p ∧ q) ⍟ (p ⊗ q) is a tautology, then ⍟ and ⊗ are respectively given by :
(a) ∧, →
(b) →, →
(c) ∨, →
(d) ∧, ∨
2. Let the tangent to the circle x2 + y2 = 25 at the point R (3, 4) meet the x-axis and y-axis at points P and Q, respectively. If r is the radius of the circle passing through the origin O and having a centre at the incentre of the triangle OPQ, then r2 is equal to:
(a) 625/72
(b) 585/66
(c) 125/72
(d) 529/64
3. Let a computer program generate only the digits 0 and 1 to form a string of binary numbers with a probability of occurrence of 0 at even places be 1/2 and probability of occurrence of 0 at the odd place be 1/3. Then the probability that ‘10’ is followed by ‘01’ is equal to :
(a) 1/6
(b) 1/18
(c) 1/9
(d) 1/3
4. The number of solutions of the equation x + 2 tan x = π/2 in the interval [0, 2π] is :
(a) 5
(b) 2
(c) 4
(d) 3
5. If the equation of the plane passing through the mirror image of a point (2, 3, 1) with respect to line 
and containing the line 
is ɑx + βy + γz = 24, then, then ɑ + β + γ is equal to:
(a) 21
(b) 19
(c) 18
(d) 20
6. Consider the function f : R → R defined by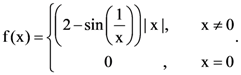 
Then f is
(a) monotonic on (0, ∞) only
(b) Not monotonic on (–∞, 0) and (0, ∞)
(c) monotonic on (–∞, 0) only
(d) monotonic on (–∞, 0) ⋃ (0, ∞)
7. Let O be the origin. Let 
x, y ∈ R, x > 0, be such that |PQ| = √20 and the vector 
is perpendicular to 
If 
z ∈ R, is coplanar with 
then the value of x2 + y2 + z2 is equal to:
(a) 2
(b) 9
(c) 1
(d) 7
8. Let L be a tangent line to the parabola y2 = 4x – 20 at (6, 2). If L is also a tangent to the ellipse 
then the value of b is equal to:
(a) 20
(b) 14
(c) 16
(d) 11
9. Let f : R → R be defined as f (x) = e–x sin x. If F : [0,1] R→ is a differentiable function such that 
then the value of 
lies in the interval
(a) [330/360, 331/360]
(b) [327/360, 329/360]
(c) [331/360, 334/360]
(d) [335/360, 336/360]
10. If x, y, z are in arithmetic progression with common difference d, x ≠ 3d, and the determinant of the matrix 
is zero, then the value of k2 is :
(a) 6
(b) 36
(c) 72
(d) 12
11. If the integral 
where ɑ, β, γ are integers and [x] denotes the greatest integer less than or equal to x, then the value of ɑ + β + γ is equal to:
(a) 20
(b) 0
(c) 25
(d) 10
12. Let y = y (x) be the solution of the differential equation cos x (3 sin x + cos x + 3) dy = (1 + y sin x (3 sin x + cos x + 3)) dx, 0 ≤ x ≤ π/2, y(0) = 0. Then, y (π/3) is equal to :
(a)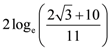 
(b) 
(c) 
(d) 
13. The value of the limit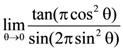 
is equal to:
(a) −1/2
(b) −1/4
(c) 0
(d) 1/4
14. If the curve y = y(x) is the solution of the differential equation 2 (x2 + x5/4) dy − y (x + x1/4) dx = 2x9/4 dx, x > 0 which passes through the point 
then the value of y(16) is equal to:
(a) 
(b) 
(c) 
(d) 
15. Let S1, S2 and S3 be three sets defined as S1 = {z ∈ C : |z – 1| ≤ √2}, S2 = {z ∈ C : Re ((1 – i) z) ≥ 1}, S3 = {z ∈ C : Im (z) ≤ 1}. Then the set S1 ⋂ S2 ⋂ S3
(a) has infinitely many elements
(b) has exactly two elements
(c) has exactly three elements
(d) is a singleton
16. If the sides AB, BC, and CA of a triangle ABC have, 3, 5 and 6 interior points respectively, then the total number of triangles that can be constructed using these points as vertices is equal to:
(a) 360
(b) 240
(c) 333
(d) 364
17. The value of 
where r is a non-zero real number and [r] denotes the greatest integer less than or equal to r, is equal to:
(a) 0
(b) r
(c) r/2
(d) 2r
18. The value of The value of 
is equal to:
(a) 1124
(b) 924
(c) 1324
(d) 1024
19. Two tangents are drawn from a point P to the circle x2 + y2 – 2x – 4y + 4 = 0, such that the angle between these tangents is
If the centre of the circle is denoted by C and these tangents touch the circle at points A and B, then the ratio of the areas of △PAB and △CAB is :
(a) 11 : 4
(b) 9 : 4
(c) 2 : 1
(d) 3 : 1
20. The number of solutions of the equation 
and [x] denotes the greatest integer less than or equal to x, is:
(a) 0
(b) 2
(c) 4
(d) Infinite
Section-B
21. Let the coefficients of third, fourth and fifth terms in the expansion of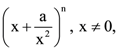 
be in the ratio 12:8:3. Then the term independent of x in the expansion is equal to ………
22. Let 
such that AB = B and a + d = 2021, then the value of ad-bc is equal to …………….
23. Let f : [–1,1] → R be defined as f (x) = ax2 + bx + c for all x ∈ [–1, 1], where a, b, c ∈ R such that f (–1) = 2, f’ (–1) = 1 and for x ∈ [–1, 1] the maximum value of f’’ (x) is 1/2. If f (x) ≤ ɑ, x ∈ [–1, 1], then the least value of ɑ is equal to …………… .
24. Let 
where n ∈ If (20)I10 = αI9 + βIB, for natural numbers α and β, then α – β equal to ………………… .
25. Let f : [−3, 1] → R be given as
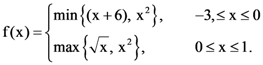
If the area bounded by y = f(x) and x-axis is A, then the value of 6A is equal to …………… .
26. Let 
be a vector in the plane containing vectors 
If the vector is perpendicular to 
and its projection on 
then the value of 
is equal to ……………… .
27. Consider a set of 3n numbers having variance 4. In this set, the mean of the first 2n numbers is 6 and the mean of the remaining n numbers is 3. A new set is constructed by adding 1 into each of the first 2n numbers and subtracting 1 from each of the remaining n numbers. If the variance of the new set is k, then 9k is equal to ………………..
28. If 1, log10(4x – 2) and 
are in arithmetic progression for a real number x, then the value of the determinant 
is equal to:
29. Let P be an arbitrary point having the sum of the squares of the distances from the planes x + y + z = 0, lx – nz = 0 and x – 2y + z = 0, equal to 9. If the locus of the point P is x2 + y2 +z2 = 9, then the value of l – n is equal to ………………
30. Let tan α, tan β and tan γ; 
be the slopes of three-line segment OA, OB and OC, respectively, where O is the origin. If the circumcentre of ∆ABC coincides with the origin and its orthocentre lies on the y-axis, then the value of 
is equal to
Latest Govt Job & Exam Updates: