VIT
Engineering Entrance Exam
Solved Paper-2013
Mathematics
1. If N denote the set of all natural numbers and R be the relation on N × N defined by (a, b) R (c, d), if ad(b + c) = bc (a + d), then R is
(a) symmetric only
(b) reflexive only
(c) transitive only
(d) an equivalence relation
2. A complex number z is such that 
The points representing this complex number will lie on
(a) an ellipse
(b) a parabola
(c) a circle
(d) a straight line
3. If a1, a2 and a3 be any positive real numbers, then which of the following statement is not true?
(a) 
(b) 
(c)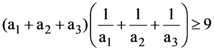 
(d) 
4. If |x2 – x – 6| = x + 2, then the value of x are
(a) –2, 2, –4
(b) –2, 2, 4
(c) 3, 2, –2
(d) 4, 4, 3
5. The centres of a set of circles, each of radius 3, lie on the circle x2 + y2 = 25. The locus of any point in the set is
(a) 
(b) 
(c) 
(d) 
6. A tower AB leans towards West making an angle α with the vertical. The angular elevation of B, the top most point of the tower is β as abserved from a point C due East of A at a distance ‘d’ from A. If the angular elevation of B from a point D due East of C at a distance 2d from C is r, then 2 tan α can be given as
(a) 3 cot β – 2 cot γ
(b) 3 cot γ – 2 cot β
(c) 3 cot β – cot γ
(d) cot β – 3 cot γ
7. If α and β are the roots of x2 – ax + b = 0 and if αn + βn = Vn, then
(a) 
(b) 
(c) 
(d) 
8. The sum of the series 
is
(a)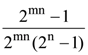 
(b)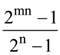 
(c) 
(d) 
9. The angle of intersection of the circles x2 + y2 – x + y – 8 = 0 and x2 + y2 + 2x + 2y – 11 = 0 is
(a) 
(b) 
(c) 
(d) 
10. The vector b = 3j + 4k is to be written as the sum of a vector b1 parallel to a = i + j and a vector b2 perpendicular to a. Then, b1 is equal to
(a) 
(b) 
(c) 
(d) 
11. If the points (x1, y1), (x2, y2) and (x3, y3) are collinear, then the rank of the matrix 
will always be less than
(a) 3
(b) 2
(c) 1
(d) None of these
12. The value of the determinant 
is
(a) 
(b) 
(c) 1
(d) 0
13. The number of integral values of K, for which the equation 7 cos x + 5 sin x = 2K + 1 has a solution, is
(a) 4
(b) 8
(c) 10
(d) 12
14. The line joining two points A(2, 0), B(3, 1) is rotated about A in anti-clockwise direction through an angle of 15°. The equation of the line in the now position is
(a) √3x – y – 2√3 = 0
(b) x – 3√y – 2 = 0
(c) √3x + y − 2√3 = 0
(d) x + √3y – 2 = 0
15. The line 2x + √6y = 2 is a tangent to the curve x2 – 2y2 = 4. The point of contact is
(a) (4, −√6)
(b) (7, −2√6)
(c) (2, 3)
(d) (√6, 1)
16. The number of integral points (integral point means both the coordinates should be integer) exactly in the interior of the triangle with vertices (0, 0), (0, 21) and (21, 0) is
(a) 133
(b) 190
(c) 233
(d) 105
17. 
is equal to
(a) 
(b) 
(c) 
(d) 
18. If f(x) = x – [x], for every real number x, where [x] is the integral part of x. Then, 
is equal to
(a) 1
(b) 2
(c) 0
(d) 1/2
19. The value of the integral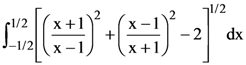 
is
(a) 
(b) 
(c) 
(d) 
20. If a tangent having slope of −4/3 to the ellipse 
intersects the major and minor axes in points A and B respectively, then the area of ∆OAB is equal to (O is centre of the ellipse)
(a) 12 sq units
(b) 48 sq units
(c) 64 sq units
(d) 24 sq units
21. The locus of mid-points of tangents intercepted between the axes of ellipse 
will be
(a)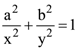 
(b) 
(c) 
(d) 
22. If PQ is a double ordinate of hyperbola 
Such that OPQ is an equilateral triangle,, O being the centre of the hyperbola, then the eccentricity ‘e’ of the hyperbola satisfies
(a) 
(b) 
(c) 
(d) 
23. The sides AB, BC and CA of a ∆ ABC have respectively 3, 4 and 5 points lying on them. The number of triangles that can be constructed using these points as vertices is
(a) 205
(b) 220
(c) 210
(d) None of these
24. In the expansion of 
the coefficient of xr is
(a) 
(b) 
(c) 
(d) 
25. If n = (1999) !, then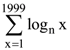 
is equal to
(a) 1
(b) 0
(c) 
(d) −1
26. P is a fixed point (a, a, a) on a line through the origin equally inclined to the axes, then any plane through P perpendicular to OP, makes intercepts on the axes, the sum of whose reciprocals is equal to
(a) a
(b) 3/2a
(c) 3a/2
(d) None of these
27. For which of the following values of m, the area of the region bounded by the curve y = x – x2 and the line y = mx equals 9/2
(a) −4
(b) −2
(c) 2
(d) 4
28. If f : R → R be such that f1/x(1) = 3 and f ′(1) = 6. Then,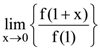 
equals to
(a) 1
(b) e1/2
(c) e2
(d) e3
29. If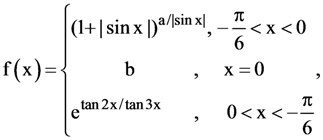 
then the value of a and b, if f is continuous at x = 0, are respectively.
(a) 
(b) 
(c) 
(d) 
30. The domain of the function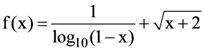 
is
(a) ] –3, –2.5[∩]–2.5, –2[
(b) [–2, 0[∩]0, 1[
(c) ]0, 1[
(d) None of the above
31. The solution of the differential equation 
is
(a) 
(b) 
(c) 
(d) 
32. If the gradient of the tangent at any point (x, y) of a curve which passes through the point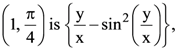 
then equation of the curve is
(a) 
(b) 
(c) 
(d) 
33. The relation R defined on set A = {x : |x| < 3, x ∈ I} by R ={(x, y) : y = |x|}
(a) {–2, 2), (–1, 1), (0, 0), (1, 1), (2, 2)}
(b) {(–2, –2), (–2, 2), (–1, 1), (0, 0), (1, –2), (1, 2), (2, –1), (2, –2)}
(c) {(0, 0), (1, 1), (2, 2)}
(d) None of the above
34. The solution of the differential equation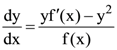 
is
(a) f(x) = y + C
(b) f(x) = y(x + C)
(c) f(x) = x + C
(d) None of the above
35. If a, b and c are in AP, then determinant 
is
(a) 0
(b) 1
(c) x
(d) 2x
36. If two events A and B. If odds against A are as 2 : 1 and those infavour of A ∪ B areas 3 : 1, then
(a) 
(b) 
(c) 
(d) 
37. The value of 2tan−1(cosec tan−1 x – tan cot−1 x) is
(a) tan−1 x
(b) tan x
(c) cot x
(d) cosec−1 x
38. The proposition ~(p ⇔ q) is equivalent to
(a) (p ⋁ ~ q) ⋀ (q ⋀ ~ p)
(b) (p ⋀ ~ q) ⋁ (q ⋀ ~ p)
(c) (p ⋀ ~q) ⋀ (q ⋀ ~ p)
(d) None of the above
39. The truth values of P be F and q be T. Then, truth vale of ~(~ p ⋁ q) is
(a) T
(b) F
(c) Either T of F
(d) Neither T nor F
40. The rate of charge of the surface area of a sphere of radius r, when the radius is increasing at the rate of 2 cm/s is proportional to
(a) 
(b) 
(c) 
(d) 
Latest Govt Job & Exam Updates: