Solved Paper-2014
VIT
Engineering Entrance Exam
Mathematics
1. If the vertices of a triangle are A(0, 4, 1), B(2, 3, −1) and C(4, 5, 0), then the orthocenter of ∆ABC, is
(a) (4, 5, 0)
(b) (2, 3, −1)
(c) (−2, 3, −1)
(d) (2, 0, 2)
2. The equation of normal to the curve y (1 + x)y + sin−1 (sin2x) at x = 0 is
(a) x + y = 1
(b) x – y = 1
(c) x + y = −1
(d) x – y = −1
3. The value of c from the Lagrange’s mean value theorem for which ![]() in [1, 5] is
in [1, 5] is
(a) 5
(b) 1
(c) √15
(d) None of these
4. If  then A ∙ (adj A) is equal to
then A ∙ (adj A) is equal to
(a) A
(b) |A|
(c) A| ∙ I
(d) None of these
5. If there is an error of k% in measuring the edge of a cube, then the per cent error in estimating its volume is
(a) k
(b) 3k
(c) k/3
(d) None of these
6. If the system of equations x + ky – z = 0, 3x – ky – z = 0 and x – 3y + z = 0, has non-zero solution, then k is equal to
(a) −1
(b) 0
(c) 1
(d) 2
7. If the points (1, 2, 3) and (2, −1, 0) lie on the opposite sides of the plane 2x + 3y – 2z = k, then
(a) k < 1
(b) k > 2
(c) k < 1 or k > 2
(d) 1 < k < 2
8. If 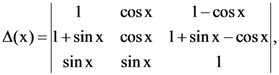 then is equal to
then is equal to
(a) 1/4
(b) 1/2
(c) 0
(d) −1/4
9. Let f ′(x), be differentiable ∀ If f(1) = −2 and f′(x) ≥ 2 ∀ x ∈ [1, 6], then
(a) f(6) < 8
(b) f(6) ≥ 8
(c) f(6) ≥ 5
(d) f(6) ≤ 5
10. If 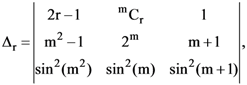 then the value of
then the value of ![]() is
is
(a) 1
(b) 0
(c) 2
(d) None of these
11. Two lines ![]() and
and ![]() intersect at a point, if k is equal to
intersect at a point, if k is equal to
(a) 2/9
(b) 1/2
(c) 9/2
(d) 1/6
12. The minimum value of ![]() is
is
(a) e
(b) 1/e
(c) e2
(d) e3
13. The triangle formed by the tangent to the curve f(x) = x2 + bx – b at the point (1, 1) and the coordinate axes lies in the first quadrant. If its area is 2, then the value of b is
(a) −1
(b) 3
(c) −3
(d) 1
14. The statement (p ⇒ q) ⇔ (~p ⋀ q) is a
(a) tautology
(b) contradiction
(c) Neither (a) nor (b)
(d) None of these
15. If ![]() then x2 + y2 is equal to
then x2 + y2 is equal to
(a) 3x – 4
(b) 4x – 3
(c) 4x + 3
(d) None of these
16. The negation of (~p ⋀ q) ⋁ (p ⋀~ q) is
(a) (p ⋁ ~q) ⋁ (~p⋁q)
(b) (p ⋁ ~q) ⋀ (~p ⋁ q)
(c) (p ⋀ ~q) ⋀ (~p ⋁ q)
(d) (p ⋀ ~q) ⋀ (p ⋁ ~q)
17. The normals at three points P, Q and R of the parabola = y2 = 4ax meet at (h, k). The centroid of the ∆PQR lies on
(a) x = 0
(b) y = 0
(c) x = −a
(d) y = a
18. The minimum area of the triangle formed by any tangent to the ellipse  with the coordinate axes is
with the coordinate axes is
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
19. If the line lx + my – n = 0 will be a normal to the hyperbola, then ![]() where k is equal to
where k is equal to
(a) n
(b) n2
(c) n3
(d) None of these
20. If cos α + i sin α, b = cos β + i sin β, c = cos γ + i sin γ and ![]() then cos(β – γ) + cos(γ – α) + cos(α – β) is equal to
then cos(β – γ) + cos(γ – α) + cos(α – β) is equal to
(a) 3/2
(b) −3/2
(c) 0
(d) 1
21. If |z + 4| ≤ 3, then the greatest and the least value of |z + 1| are
(a) −1, 6
(b) 6, 0
(c) 6, 3
(d) None of these
22. The angle between lines joining the origin to the point of intersection of the line √3x + y = 2 and the curve y2 – x2 = 4 is
(a) ![]()
(b) π/6
(c) 
(d) π/2
23. If the area of the triangle on the complex plane formed by the points z, z + iz and iz is 200, then the value of 3|z| must be equal to
(a) 20
(b) 40
(c) 60
(d) 80
24. Equation of the chord of the hyperbola 25x2 – 16y2 = 400 which is bisected at the point (6, 2), is
(a) 6x – 7y = 418
(b) 75x – 16y = 418
(c) 25x – 4y = 400
(d) None of these
25. If a plane meets the coordinates axes at A, B and C such that the centroid of the triangle is (1, 2, 4), then the equation of the plane is
(a) x + 2y + 4z = 12
(b) 4x + 2y + z = 12
(c) x + 2y + 4z = 3
(d) 4x + 2y + z = 3
26. The volume of the tetrahedron include between the plane 3x + 4y – 5z – 60 = 0 and the coordinate planes is
(a) 60
(b) 600
(c) 720
(d) 400
27. ![]() is equal to
is equal to
(a) 0
(b) 4
(c) 8
(d) 1
28. The value of ![]() where [∙] is the greatest integer function, is
where [∙] is the greatest integer function, is
(a) 2 – √2
(b) 2 + √2
(c) √2 – 1
(d) √2 – 2
29. If ![]() then the expression for l(m, n) in terms of l(m + 1, n+1) is
then the expression for l(m, n) in terms of l(m + 1, n+1) is
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
30. The area in the first quadrant between x2 + y2 = π2 and y = sin x is
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
31. The area bounded y = xe|x| and lines |x| = 1, y = 0 is
(a) 4 sq units
(b) 6 sq units
(c) 1 sq unit
(d) 2 sq units
32. The solution of 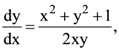 satisfying y(1) = 0 is given by
satisfying y(1) = 0 is given by
(a) hyperbola
(b) circle
(c) ellipse
(d) parabola
33. If 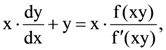 then f(xy) is equal to
then f(xy) is equal to
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
34. The differential equation of the rectangular hyperbola, where axes are the asymptotes of the hyperbola, is
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
35. The length of longer diagonal of the parallelogram constructed on 5a + 2b and a – 3b, if it is given that |a| = 2√2, |b| = 3 and the angle between a and b is π/4, is
(a) 15
(b) √113
(c) √593
(d) √369
36. If r = αb × c + βc × a + γa × b and [a b c] = 1, then α + β + γ is equal to
(a) r ∙ [b × c + c × a + a × b]
(b) ![]()
(c) 2r ∙ (a + b + c)
(d) 4
37. If a, b, c are three non-coplanar vectors and p , q, r are reciprocal vectors, then (la + mb + nc) ∙ (lp + mq + nr) is equal to
(a) l + m +n
(b) 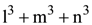
(c) ![]()
(d) None of these
38. If the integers m and n are chosen at random from 1 to 100, then the probability that a number of the form 7n + 7m is divisible by 5, equals to
(a) 1/4
(b) 1/2
(c) 1/8
(d) 1/3
39. Let X denote the sum of the numbers obtained when two fair dice are rolled. The variance and standard deviation of X are
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
40. A four-digit number is formed by the digits 1, 2, 3, 4 with no repetition. The probability that the number is odd, is
(a) zero
(b) 1/3
(c) 1/4
(d) None of these
Latest Govt Job & Exam Updates: