Solved Paper -2015
VIT
Engineering Entrance Exam
Mathematics
1. If the matrix 
then adj (adj A) is equal to
(a)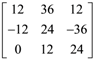 
(b)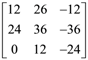 
(c)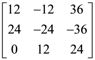 
(d) 
2. Which of the following options is not the asymptote of the curve 3x2 + 2x2y – 7xy2 + 2y3 – 14xy + 7y2 + 4x + 5y = 0?
(a) 
(b) 
(c) 
(d) 
3. If N is a set of natural numbers, then under binary operation a ∙ b = a + b, (N, ∙) is
(a) quasi-group
(b) semi-group
(c) monoid
(d) group
4. 
(a) 
(b) 
(c) 
(d) 
5. If (2, 7, 3) is one end of a diameter of the sphere x2 + y2 + z2 – 6x – 12y – 2z + 20 = 0, then the coordinates of the other end of the diameter are
(a) (−2, 5, −1)
(b) (4, 5, 1)
(c) (2, −5, 1)
(d) (4, 5, −1)
6. The two lines x = my + n, z = py + q and x = m′y + n′, z = p′y + q′ are perpendicular to each other, if
(a) 
(b) 
(c) 
(d) 
7. A tetrahedron has vertices at O(0, 0, 0), A(−2, 1), B(−2, 1, 1) and C(1, −1, 2). Then, the angle between the faces OAB and ABC will be
(a) 
(b) 
(c) 
(d) 
8. If a line segment OP makes angle of 
with X-axis and Y-axis, respectively. Then, the direction cosines are
(a) 
(b) 
(c) 
(d) 
9. If p, q, r are simple propositions with truth values T, F, T, then the truth value of (~p ⋁ q) ⋀ ~ r ⇒ p is
(a) true
(b) false
(c) true, if r is false
(d) true, if q is true
10. On the interval [0, 1], the function x25(1 – x)75 takes its maximum value at the point
(a) 0
(b) 1/4
(c) 1/2
(d) 1/3
11. If |z| ≥ 3, then the least value of 
is
(a) 11/2
(b) 11/4
(c) 3
(d) 1/4
12. The normal at the point (at21, 2at1) on the parabola meets the parabola again in the point (at22, 2at2), then
(a) 
(b) 
(c) 
(d) 
13. If 
then the angle θ between a and b is given by
(a) 
(b) 
(c) 
(d) 
14. The area bounded by the curves y = cos x and y = sin x between the ordinates x = 0 and 
is
(a) (4√2 – 2) sq units
(b) (4√2 + 2) sq units
(c) (4√2 – 1) sq units
(d) (4√2 + 1) sq units
15. If a, b and c are three non-coplanar vectors, then (a + b – c) ∙ [(a – b) × (b – c)] equals
(a) 0
(b) a ∙ b × c
(c) a ∙ c × b
(d) 3a ∙ b × c
16. If there is an error of m% in measuring the edge of cube, then the per cent error in estimating its surface area is
(a) 2 m
(b) 3 m
(c) 1 m
(d) 4 m
17. If the rectangular hyperbola is x2 – y2 = 64. Then, which of the following is not correct?
(a) The length of latusrectum is 16
(b) The eccentricity is √2
(c) The asymptotes are parallel to each other
(d) The directrices are x = ±4√2
18. The equation of tangents to the hyperbola 3x2 – 2y2 = 6, which is perpendicular to the line x – 3y = 3, are
(a) y = −3x ± √15
(b) y = 3x ± √6
(c) y = −3x ± √6
(d) y = 2x ± √15
19. 
is equal to
(a) 1
(b) 0
(c) −2
(d) −1
20. The area of the region bounded by the curves x2 + y2 = 9 and x + y = 3 is
(a) 
(b) 
(c) 
(d) 
21. For any three vectors a, b and [a + b, b +c, c + a] is
(a) [a b c]
(b) 3[a b c]
(c) 2[a b c]
(d) 0
22. 
is equal to
(a) 0
(b) 2
(c) 4
(d) 7
23. If the mean and variance of a binomial distribution are 4 and 2, respectively. Then, the probability of atleast 7 successes is
(a) 
(b) 
(c) 
(d) 
24. The shortest distance between the lines 
and 
is
(a) 
(b) 
(c) 
(d) 
25. If a plane passing through the point (2, 2, 1) and is perpendicular to the planes 3x + 2y + 4z + 1 = 0 and 2x + y + 3z + 2 = 0. Then, the equation of the plane is
(a) 2x – y – z – 1 = 0
(b) 2x + 3y + z – 1 = 0
(c) 2x + y + z + 3 = 0
(d) x – y + z – 1 = 0
26. From a city population, the probability of selection a sale or smoker is 7/10, a male smoker is 2/5 and a male, if a smoker is already selected, is 2/3. Then, the probability of
(a) selecting a male is 3/2
(b) selecting a smoker is 1/5
(c) selecting a non-smoker is 2/5
(d) selecting a smoker, if a male is first selected, is given by 8/5
27. At t = 0, the function 
has
(a) a minimum
(b) a discontinuity
(c) a point of inflexion
(d) a maximum
28. Using Rolle’s theorem, the equation a0xn + a1xn−1 + … + an = 0 has atleast one root between 0 and 1, if
(a) 
(b) 
(c) 
(d) 
29. Which of the following inequality is true for x > 0?
(a) 
(b) 
(c) 
(d) 
30. The solution of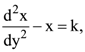 
where k is non=zero constant, vanishes when y = 0 and tends of finite limit as y tends to infinity, is
(a) 
(b) 
(c) 
(d) 
31. The differential equation (3x + 4y + 1) dx + (4x + 5y + 1) dy =0 represents a family of
(a) circles
(b) parabolas
(c) ellipses
(d) hyperbolas
32. If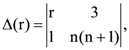 
then 
is equal to
(a) 
(b) 
(c) 
(d) 
33. If A, B, C are three events associated with a random experiment, then 
is
(a) P(A⋃B⋃C)
(b) P(∩B∩C)
(c) 
(d) 
34. If 
then rank (A) is equal to
(a) 4
(b) 1
(c) 2
(d) 3
35. The probability of atleast one double six being thrown in n throws with two ordinary dice is greater than 99%.
Then, the least numerical value of n is
(a) 100
(b) 164
(c) 170
(d) 184
36. Find the value of k for which the simultaneous equations x + y + z =3; x + 2y + 3z = 4 and x + 4y + kz = 6 will not have a unique solution.
(a) 0
(b) 5
(c) 6
(d) 7
37. If the complex number z lies on a circle with centre at the origin and radius 1/4, then the complex number −1 + 8z lies on a circle with radius
(a) 4
(b) 1
(c) 3
(d) 2
38. If line y = 2x + C is a normal to the ellipse 
then
(a) 
(b) 
(c) 
(d)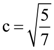 
39. If x2 + x + 1 = 0, then the value of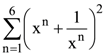 
is
(a) 13
(b) 12
(c) 9
(d) 14
40. If p : It rains today, q : I go to school, r : I shall meet any friends and s : I shall go for a movie then which of the following is the proportion?
If it does not rain or if I do not go to school then I shall meet my friend and go for a movie.
(a) (~p ⋀ ~ q) ⇒ (r ⋀ s)
(b) (~p ⋀ q) ⇒ (r ⋀ s)
(c) (~p ⋁ q) ⇒ (r ⋁ s)
(d) None of these
Latest Govt Job & Exam Updates: