VITEE-2016 Solved Paper

PART III MATHEMATICS

1. The solution of the differential equation

(a)

(b)

(c)

(d)

Ans: (b)

2. A tetrahedron has vertices at O(0, 0, 0), A(1, 2, 1) B(2, 1, 3) and C(−1, 1, 2). Then the angle between the faces OAB and ABC will be

(a) 120°

(b) cos⁻¹(17/31)

(d) 90°

Ans: (a)

3. The foci of the ellipse and the hyperbola coincide then value of b² is

(a) 1

(b) 5

(d) 9

Ans: (c)

4. If the tangent to the function y = f(x) at (3, 4) makes an angle of 3π/4 with the positive direction of x-axis in anticlockwise direction then f ʹ(3) is

(a) −1

(b) 1

(d) √3

Ans: (a)

5. The probability of India winning a test match against Australia is 1/2 assuming independence from match to match. The probability that in a match series India’s second win occurs at third test match is

(a) 1/8

(b) 1/4

(d) 2/3

Ans: (b)

6. If then the value of is (given that

(a) −7

(b) 7

(d) −14

Ans: (b)

7. If f(x) = x²_,g(x) = 2x, 0 ≤ x ≤ 2 then the value of 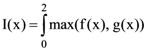is

(a) 10/3

(b) 1/3

(d) 32

Ans: (d)

8. If A and B are matrices and B = ABA⁻¹ then the value of (A + B) (A – B) is

(a) A² + B²

(b) A² – B²

(d) A – B

Ans: (b)

9. The value of (1 + ω –ω²)⁷ is

(a) 128ω²

(b) −128ω²

(d) −128ω

Ans: (b)

10. The moment about the point acting through the point 2i + 3j + k is

(a)

(b)

(c)

(d)

Ans: (d)

11. If g(x) is a polynomial satisfying g(x) g(y) = g(x) + g(y) + g(xy) – 2 for all real x and y and g(2) = 6 then is

(a) 9

(b) 10

(d) 20

Ans: (b)

12. The equation of one of the common tangents to the parabola y² = 8x and x² + y² – 12x + 4 = 0 is

(a) y = x + 2

(b) y = x – 2

(d) None of these

Ans: (c)

13. If then the value of y is

(a)

(b)

(c)

(d)

Ans: (b)

14. What is the area of a loop of the curve r = a sin 3θ?

(a)

(b)

(c)

(d)

Ans: (d)

15. Convert the hexadecimal numeral ABCD into binary numeral

(a) (1010101111001101)₂

(b) (1001000011111111)₂

(d) (1000100100111100)₂

Ans: (a)

16. The normal at the point (at₁², 2at₁) on the parabola, cuts the parabola again at the point whose parameter is

(a)

(b)

(c)

(d)

Ans: (c)

17. The distance moved by the particle in time t is given by s = t³ – 12t² + 6t + 8. At the instant, when its acceleration is zero the velocity is :

(a) 42

(b) −42

(d) −48

Ans: (b)

18. The logical expression X, in its simplest form for the truth table

(a) X = a, b

(b) X = a + b

(d) X = a.b’

Ans: (a)

19. The value of is equal to

(a) −3/4

(b) 3/4

(d) 1/4

Ans: (b)

20. Consider the objective function Z = 40x + 50y. The minimum number of constraints that are required to maximize Z are

(a) 4

(b) 2

(d) 1

Ans: (c)

21. In a culture the bacteria count is 1,00,000. The number is increased by 10% in 2 hours. In how many hours will the count reach 2,00,000 if the rate of growth of bacteria is proportional to the number present.

(a)

(b)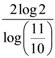

(c)

(d)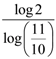

Ans: (b)

22. The value of is

(a) π/6

(b) π/4

(d) π/2

Ans: (b)

23. If a = cos 2α + i sin 2α, b = cos 2β + i sin 2β, c = cos 2γ + i sin 2γ and d = cos 2δ + i sin 2δ, then

(a) √2 cos(α + β + γ + δ)

(b) 2 cos (α + β + γ + δ)

(d) None of these

Ans: (b)

24. If the mean of a binomial distribution is 25, then its standard deviation lies in the interval

(a) [0, 5)

(b) (0, 5]

(d) (0, 25]

Ans: (a)

25. Number of ways of selecting three squares on a chessboard so that all the three be on a diagonal line of the board or parallel to it is

(a) 196

(b) 126

(d) 392

Ans: (d)

26. If A and B are two matrices such than rank of A = m and rank of B = n, then

(a) rank (AB) = mn

(b) ran (AB) ≥ ran (A)

(d) rank (AB) ≤ min (rank A, rank B)

Ans: (d)

27. A variable plane remains at constant distance p from the origin. If it meets coordinate axes at points A, B, C then the locus of the centroid of ∆ ABC is

(a) x⁻² + y⁻² + z⁻² = 9p⁻²

(b) x⁻³ + y⁻³ + z⁻³ = 9p⁻³

(d) x³ + y³ + z³ = 9p³

Ans: (a)

28. While shuffling a pack of 52 playing cards, 2 are accidentally dropped. The probability that the missing cards to be of different colours is

(a) 29/52

(b) 1/2

(d) 27/51

Ans: (c)

29. Which of the following is INCORRECT for the hyperbola x² – 2y² – 2x + 8y – 1 = 0

(a) It eccentricity is √2

(b) Length of the transverse axis is 2√3

(d) Latus rectum is 4√3

Ans: (a)

30. A box contains 20 identical balls of which 10 are blue and 10 are green. The balls are drawn at random from the box one at a time with replacement. The probability that a blue ball is drawn 4^th time on the 7^th draw is

(a) 27/32

(b) 5/64

(d) 1/2

Ans: (c)

31. The number of common tangents to the circles x² + y² – 6x – 14y + 48 = 0 and x² + y² – 6x = 0 is

(a) 1

(b) 2

(d) 4

Ans: (d)

32. The solution of the equation cos²θ + sin θ + 1 = 0, lies in the interval

(a)

(b)

(c)

(d)

Ans: (d)

33. If f(x) = (1 + x)^2/x for x ≠ 0 and f(0) = e² is

(a) left continuous only at x = 0

(b) right continuous only at x = 0

(d) discontinuous at x = 0

Ans: (c)

34. If y = y^x/lnx then at x = e is

(a) e

(b) 2^e log 2

(d) 0

Ans: (d)

35. is equal to

(a)

(b)

(c)

(d)

Ans: (d)

36. If the letters of the word KRISNA are arranged in all possible ways and these words are written out as a in a dictionary, then the rank of the word KRISNA is

(a) 324

(b) 341

(d) None of these

Ans: (a)

37. The shortest distance between the lines x = y + 2 = 6z – 6 and x + 1 = 2y = −12z is

(a) 1/2

(b) 2

(d) 3/2

Ans: (b)

38. The domain and range of the function f given by f(x) = 2 – |x – 5| is

(a) Domain = R⁺, Range = (−∞, 1]

(b) Domain = R, Range = (−∞, 2)

(d) Domain = R⁺, Range = (−∞, 2]

Ans: (b)

39. The number of surjective function from A to B where A = A{1, 2, 3, 4} and B = {a, b} is

(a) 14

(b) 12

(d) 15

Ans: (a)

40. If f(a + b – x) = f(x), then 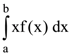is equal to

(a)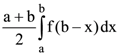

(b)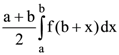

(c)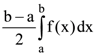

(d)

Ans: (d)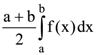

Latest Govt Job & Exam Updates:

VITEEE 2016 Previous Year Mathematics Question Paper With Answer Key

View Full List ...