JEE Main Offline Examination Held on 08-04-2018 Code A
1. The density of a material in the shape of a cube is determined by measuring three sides of the cube and its mass. If the relative errors in measuring the mass and length are respectively 1.5% and 1%, the maximum error in determining the density is
(1) 2.5%
(2) 3.5%
(3) 4.5%
(4) 6%
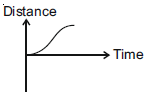
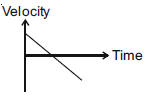
2. All the graphs below are intended to represent the same motion. One of them does it incorrectly. Pick it up.
(1) 
(2) 
(3) 
(4) 
3. Two masses m1= 5 kg and m2= 10 kg, connected by an inextensible string over a frictionless pulley, are moving as shown in the figure. The coefficient of friction of horizontal surface is 0.15. The minimum weight m that should be put on top of m2 to stop the motion is
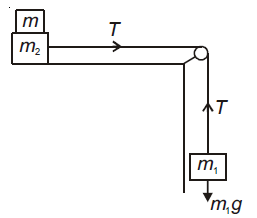
(1) 18.3 kg
(2) 27.3 kg
(3) 43.3 kg
(4) 10.3 kg
4. A particle is moving in a circular path of radius a under the action of an attractive potential 
Its total energy is
(1) 
(2) 
(3) Zero
(4) 
5. In a collinear collision, a particle with an initial speed v0 strikes a stationary particle of the same mass. If the final total kinetic energy is 50% greater than the original kinetic energy, the magnitude of the relative velocity between the two particles, after collision, is
(1) 
(2) 
(3) 
(4) 
6. Seven identical circular planar disks, each of mass M and radius R are welded symmetrically as shown. The moment of inertia of the arrangement about the axis normal to the plane and passing through the point P is
(1) 
(2) 
(3) 
(4) 
7. From a uniform circular disc of radius R and mass 9M, a small disc of radius R/3 is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is
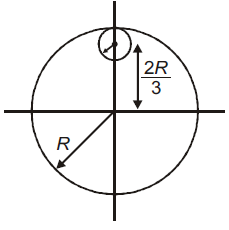
(1) 4MR2
(2) 
(3) 10MR2
(4) 
8. A particle is moving with a uniform speed in a circular orbit of radius R in a central force inversely proportional to the nth power of R. If the period of rotation of the particle is T, then
(1) T ∝ R3/2 for any n
(2) 
(3) T ∝ R(n + 1)/2
(4) T ∝ Rn/2
9. A solid sphere of radius r made of a soft material of bulk modulus K is surrounded by a liquid in a cylindrical container. A massless piston of area of a floats on the surface of the liquid, covering entire cross-section of cylindrical container. When a mass m is placed on the surface of the piston to compress the liquid, the fractional decrement in the radius of the sphere, (dr/r), is
(1) 
(2) 
(3) 
(4) 
10. Two moles of an ideal monoatomic gas occupies a volume V at 27°C. The gas expands adiabatically to a volume 2 V. Calculate (a) the final temperature of the gas and (b) change in its internal energy.
(1) (a) 189 K (b) 2.7 kJ
(2) (a) 1195 K (b) −2.7 kJ
(3) (a) 189 K (b) −2.7 kJ
(4) (a) 195 K (b) 2.7 kJ
11. The mass of a hydrogen molecule is 3.32 × 10−27 If 1023 hydrogen molecules strike, per second, a fixed wall of area 2 cm2 at an angle of 45° to the normal, and rebound elastically with a speed of 103 m/s, then the pressure on the wall is nearly
(1) 2.34 × 103 N/m2
(2) 4.70 × 103 N/m2
(3) 2.35 × 102 N/m2
(4) 4.70 × 102 N/m2
12. A silver atom in a solid oscillates in simple harmonic motion in some direction with a frequency of 1012/second. What is the force constant of the bonds connecting one atom with the other? (Mole wt. of silver = 108 and Avagadro number = 6.02 × 1023 gm mole−1)
(1) 6.4 N/m
(2) 7.1 N/m
(3) 2.2 N/m
(4) 5.5 N/m
13. A granite rod of 60 cm length is clamped at its middle point and is set into longitudinal vibrations. The density of granite is 2.7 × 103 kg/m3 and its Young’s modulus is 9.27 × 1010 What will be the fundamental frequency of the longitudinal vibrations?
(1) 5 kHz
(2) 2.5 kHz
(3) 10 kHz
(4) 7.5 kHz
14. Three concentric metal shells A, B and C of respective radii a, b and c (a < b < c) have surface charge densities +σ, −σ and + σ respectively. The potential of shell B is
(1) 
(2) 
(3) 
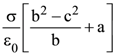
(4) 
15. A parallel plate capacitor of capacitance 90 pF is connected to a battery of emf 20 V. If a dielectric material of dielectric constant K = 5/3 is inserted between the plates, the magnitude of the induced charge will be
(1) 1.2 nC
(2) 0.3 nC
(3) 2.4 nC
(4) 0.9 nC
16. In an a.c. circuit, the instantaneous e.m.f. and current are given by
e = 100 sin 30t
In one cycle of a.c., the average power consumed by the circuit and the wattless current are, respectively
(1) 50, 10
(2) 
(3) 
(4) 50, 0
17. Two batteries with e.m.f 12 V and 13 V are connected in parallel across a load resistor of 10 Ω. The internal resistances of the two batteries are 1 Ω and 2 Ω respectively. The voltage across the load lies between
(1) 11.6 V and 11.7 V
(2) 11.5 V and 11.6 V
(3) 11.4 V and 11.5 V
(4) 11.7 V and 11.8 V
18. An electron, a proton and an alpha particle having the same kinetic energy are moving in circular orbits of radii re, rp, rα respectively in a uniform magnetic field B. The relation between re, rp, rα is
(1) re > rp = rα
(2) re < rp = rα
(3) re < rp < rα
(4) re < rα < rp
19. The dipole moment of a circular loop carrying a current I, is m and the magnetic field at the centre of the loop is B1. When the dipole moment is doubled by keeping the current constant, the magnetic field at the centre of the loop is B2. The ratio B1/B2 is
(1) 2
(2) 
(3) 
(4) 
20. For an RLC circuit driven with voltage of amplitude vm and frequency 
the current exhibits resonance. The quality factor, Q is given by
(1) 
(2) 
(3) 
(4) 
21. An EM wave from air enters a medium. The electric fields are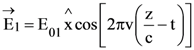 
in air and 
in medium, where the wave number k and frequency ν refer to their values in air. The medium is non-magnetic. If 
refer to relative permittivities of air and medium respectively, which of the following options is correct?
(1) 
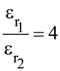
(2) 
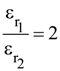
(3) 
(4) 
22. Unpolarized light of intensity I passes through an ideal polarizer A. Another identical polarizer B is placed behind A. The intensity of light beyond B is found to be I/2. Now another identical polarizer C is placed between A and B. The intensity beyond B is now found to be I/8. The angle between polarizer A and C is
(1) 0°
(2) 30°
(3) 45°
(4) 60°
23. The angular width of the central maximum in a single slit diffraction pattern is 60°. The width of the slit is 1 μm. The slit is illuminated by monochromatic plane waves. If another slit of same width is made near it, Young’s fringes can be observed on a screen placed at a distance 50 cm from the slits. If the observed fringe width is 1 cm, what is slit separation distance?
(i.e. distance between the centres of each slit.)
(1) 25 μm
(2) 50 μm
(3) 75 μm
(4) 100 μm
24. An electron from various excited states of hydrogen atom emit radiation to come to the ground state. Let λn, λg be the de Broglie wavelength of the electron in then nth state and the ground state respectively. Let Λn be the wavelength of the emitted photo in the transition from the nth state to the ground state. For large n, (A, B are constants)
(1) 
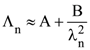
(2) Λn ≈ A + Bλn
(3) 
(4) 
25. If the series limit frequency of the Lyman series is νL, then the series limit frequency of the P fund series is
(1) 25 νL
(2) 16 νL
(3) νL/16
(4) νL/25
26. It is found that if a neutron suffers an elastic collinear collision with deuterium at rest, fractional loss of its energy is pd; while for its similar collision with carbon nucleus at rest, fractional loss of energy is pd and pc are respectively
(1) (.89, .28)
(2) (.28, .89)
(3) (0, 0)
(4) (0, 1)
27. The reading of the ammeter for a silicon diode in the given circuit is
(1) 0
(2) 15 mA
(3) 11.5 mA
(4) 13.5 mA
28. A telephonic communication service is working at carrier frequency of 10 GHz. Only 10% of it is utilized for transmission. How many telephonic channels can be transmitted simultaneously if each channel requires a bandwidth of 5 kHz?
(1) 2 × 103
(2) 2 × 104
(3) 2 × 105
(4) 2 × 106
29. In a potentiometer experiment, it is found that no current passes through the galvanometer when the terminals of the cell are connected across 52 cm of the potentiometer wire. If the cell is shunted by a resistance of 5 Ω, a balance is found when the cell is connected across 40 cm of the wire. Find the internal resistance of the cell.
(1) 1 Ω
(2) 1.5 Ω
(3) 2 Ω
(4) 2.5 Ω
30. On interchanging the resistances, the balance point of a meter bridge shifts to the left by 10 cm. The resistance of their series combination is 1 kΩ. How much was the resistance on the left slot before interchanging the resistances?
(1) 990 Ω
(2) 505 Ω
(3) 550 Ω
(4) 910 Ω
31. The ratio of mass percent of C and H of an organic compound (CXHYOZ) is 6 : 1. If one molecule of the above compound (CXHYOZ) contains half as much oxygen as required to burn one molecule of compound CXHY completely CO2 and H2 The empirical formula of compound CXHYOZ is
(1) C3H6O3
(2) C2H4O
(3) C3H4O2
(4) C2H4O3
32. Which type of ‘defect’ has the presence of cations in the interstitial sites?
(1) Schottky defect
(2) Vacancy defect
(3) Frenkel defect
(4) Metal deficiency defect
33. According to molecular orbital theory, which of the following will not be a viable molecule?
(1) 
(2) 
(3) 
(4) 
34. Which of the following lines correctly show the temperature dependence of equilibrium constant K, for an exothermic reaction?
(1) A and B
(2) B and C
(3) C and D
(4) A and D
35. The combustion of benzene (l) gives CO2 (g) and H2O(I). Given that heat of combustion of benzene at constant volume is –3263.9 kJ mol−1 at 25°C; heat of combustion (in kJ mol−1) of benzene at constant pressure will be
(R = 8.314 JK−1 mol−1)
(1) 4152.6
(2) −452.46
(3) 3260
(4) −3267.6
36. For 1 molal aqueous solution of the following compounds, which one will show the highest freezing point?
(1) [Co(H2O)6]Cl3
(2) [Co(H2O)5Cl]Cl2 ∙ H2O
(3) [Co(H2O)4Cl2]Cl ∙ 2H2O
(4) [Co(H2O)3Cl3] ∙ 3H2O
37. An aqueous solution contains 0.10 M H2S and 0.20 M HCl. If the equilibrium constant for the formation of HS− from H2S is 1.0 × 10−7 and that of S2− from HS− ions is 1.2 × 10−13 then the concentration of S2− ions in aqueous solution is
(1) 5 × 10−8
(2) 3 × 10−20
(3) 6 × 10−21
(4) 5 × 10−19
38. An aqueous solution contains an unknown concentration of Ba2+. When 50 mL of a 1 M solution of Na2SO4 is added, BaSO4 just begins to precipitate. The final volume is 500 mL. The solubility product of BaSO4 is 1 × 10−10. What is original concentration of Ba2+?
(1) 5 × 10−9 M
(2) 2 × 10−9 M
(3) 1.1 × 10−9 M
(4) 1.0 × 10−10 M
39. At 518°C, the rate of decomposition of a sample of gaseous acetaldehyde, initially at a pressure of 363 torr, was 1.00 torr s−1 when 5% had reacted and 0.5 torr s−1 when 33% had reacted. The order of the reaction is
(1) 2
(2) 3
(3) 1
(4) 0
40. How long (approximate) should water be electrolysed by passing through 100 amperes current so that the oxygen released can completely burn 27.66 g of diborane? (Atomic weight of B = 10.8 u)
(1) 6.4 hours
(2) 0.8 hours
(3) 3.2 hours
(4) 1.6 hours
41. The recommended concentration of fluoride ion in drinking water is up to 1 ppm as fluoride ion is required to make teeth enamel harder by converting [3Ca3(PO4)2 . Ca(OH)2] to
(1) [CaF2]
(2) [3(CaF2). Ca(OH)2]
(3) [3Ca3(PO4)2. CaF2]
(4) [3{Ca(OH)2}. CaF2]
42. Which of the following compounds contain(s) no covalent bond(s)?
KCl, PH3, O2, B2H6, H2SO4
(1) KCl, B2H6, PH3
(2) KCl2, H2SO4
(3) KCl
(4) KCl, B2H2
43. Which of the following are Lewis acids?
(1) PH3 and BCl3
(2) AlCl3 and SiCl4
(3) PH3 and SiCl4
(4) BCl3 and AlCl3
44. Total number of lone pair of electron in 
ion is
(1) 3
(2) 6
(3) 9
(4) 12
45. Which of the following salts is the most basic in aqueous solution?
(1) Al(CN)3
(2) CH3COOK
(3) FeCl3
(4) Pb(CH3COO)2
46. Hydrogen peroxide oxidises [Fe(CN)6]4− to [Fe(CN)6] 3− in acidic medium but reduces [Fe(CN)6] 3− to [Fe(CN)6] 4− in alkaline medium. The other product formed are, respectively.
(1) (H2O + O2) and H2O
(2) (H2O + O2) and (H2O + OH–)
(3) H2O and (H2O + O2)
(4) H2O and (H2O + OH–)
47. The oxidation states of
Cr in [Cr(H2O)6]Cl3, [Cr(C6H6)2], and K2[Cr(CN)2(O)2 (NH3)] respectively are
(1) +3 , +4 and +6
(2) +3, +2, and +4
(3) +3, 0and +6
(4) +3, 0 and +4
48. The compound that does not produce nitrogen gas by the thermal decomposition is
(1) Ba(N3)2
(2) (NH4)2Cr2O7
(3) NH4NO2
(4) (NH4)2SO4
49. When metal ‘M’ is treated with NaOH, a white gelatinous precipitate ‘X’ is obtained, which is soluble in excess of NaOH. Compound ‘X’ when heated strongly gives an oxide which is used in chromatography as an adsorbent. The metal ‘M’ is
(1) Zn
(2) Ca
(3) Al
(4) Fe
50. Consider the following reaction and statements
[Co(NH3)4Br2]+ + Br− → [Co(NH3)3Br3] + NH3
(I) Two isomers are produced if the reactant complex ion is a cis-isomer
(II) Two isomers are produced if the reactant complex ion is a trans-isomer.
(III) Only one isomer is produced if the reactant complex ion is a trans-isomer.
(IV) Only one isomer is produced if the reactant complex ion is a cis-isomer.
The correct statements are:
(1) (I) and (II)
(2) (I) and (III)
(3) (III) and (IV)
(4) (II) and (IV)
51. Glucose on prolonged heating with HI gives
(1) n-Hexane
(2) 1-Hexene
(3) Hexanoic acid
(4) 6-iodohexanal
52. The trans-alkenes are formed by the reduction of alkynes with
(1) H2 – Pd/C, BaSO4
(2) NaBH4
(3) Na/liq. NH3
(4) Sn – HCl
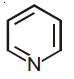
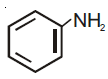
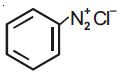
53. Which of the following compounds will be suitable for Kjeldahl’s method for nitrogen estimation?
(1) 
(2) 
(3) 
(4) 
54. Phenol on treatment with CO2 in the presence of NaOH followed by acidification produces compound X as the major product. X on treatment with (CH3CO)2O in the presence of catalytic amount of H2SO4 produces
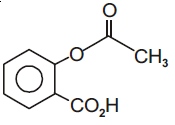
(1) 
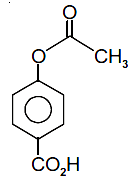
(2) 
(3) 
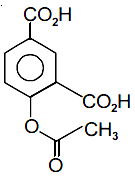
(4) 
55. An alkali is titrated against an acid with methyl orange as indicator, which of the following is a correct combination?
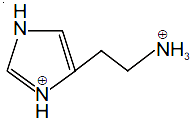
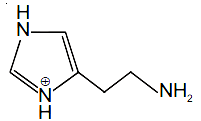
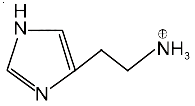
56. The predominant form of histamine present in human blood is (pKa, Histidine = 6.0)
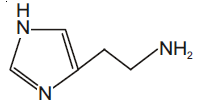
(1) 
(2) 
(3) 
(4) 
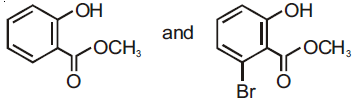
57. Phenol reacts with methyl chloroformate in the presence of NaOH to form product A. A reacts with Br2 to form product B. A and B are respectively
(1) 
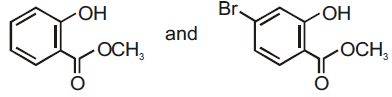
(2) 
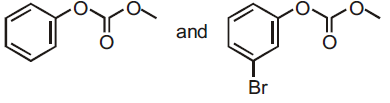
(3) 
(4) 
58. The increasing order of basicity of the following compound is
(1) (a) < (b) < (c) < (d)
(2) (b) < (a) < (c) < (d)
(3) (b) < (a) < (d) < (c)
(4) (d) < (b) < (a) < (c)
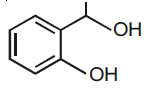
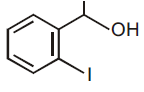
59. The major product formed in the following reaction is
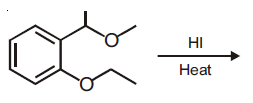
(1) 
(2) 
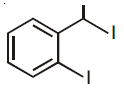
(3) 
(4) 
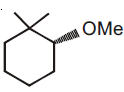
60. The major product of the following reaction is
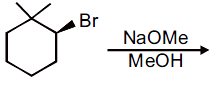
(1) 
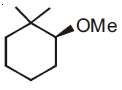
(2) 
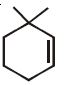
(3) 
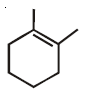
(4) 
61. Two sets A and B are as under :
A = {(a, b) ∈ R × R : |a – 5| < 1 and |b – 5| < 1}
B = {(a, b) ∈ R × R : 4(a – 6)2 + 9(b – 5)2 ≤ 36},
then
(1) B ⊂ A
(2) A ⊂ B
(3) A ∩ B = ϕ (an empty set)
(4) Neither A ⊂ B nor B ⊂ A
62. Let S = {x ∈ R : x ≥ 0 and 2|√x – 3| + √x(√x – 6) + 6 = 0}. Then S :
(1) Is an empty set
(2) Contains exactly one element
(3) Contains exactly two elements
(4) Contains exactly four elements
63. If α, β ∈ C are the distinct roots, of the equation x2 – x + 1= 0, then α101 + β107 is equal to
(1) −1
(2) 0
(3) 1
(4) 2
64. If 
then the ordered pair (A, B) is equal to
(1) (−4, −5)
(2) (−4, 3)
(3) (−4, 5)
(4) (4, 5)
65. If the system of linear equations
x + ky + 3z = 0
3x + ky – 2z = 0
2x + 4y – 3z = 0
has a non-zero solution (x, y, z), then xz/y2 is equal to
(1) –10
(2) 10
(3) –30
(4) 30
66. From 6 different novels and 3 different dictionaries, 4 novels and 1 dictionary are to be selected and arranged in a row on a shelf so that the dictionary is always in the middle. The number of such arrangements is
(1) At least 1000
(2) Less then 500
(3) At least 500 but less than 750
(4) At least 750 but less than 1000
67. The sum of the co-efficients of all odd degree terms in the expansion of 
is
(1) −1
(2) 0
(3) 1
(4) 2
68. Let a1, a2, a3, …….., a49 be in A.P. such that
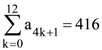and a9 + a43 = 66.
If 
then m is equal to
(1) 66
(2) 68
(3) 34
(4) 33
69. Let A be the sum of the first 20 terms and B be the sum of the first 40 terms of the series 12 + 2.22 + 32 + 2.42 + 52 + 2.62 + ….
If B – 2A = 100λ, then λ is equal to
(1) 232
(2) 248
(3) 464
(4) 496
70. For each t ∈ R, let [t] be the greatest integers less than or equal to t. Then
(1) Is equal to 0
(2) Is equal to 15
(3) Is equal to 120
(4) Does not exist (in R)
71. Let S = {t ∈ R : f(x) = |x – π| ∙(|x| – 1)sin |x| is not differential at t}. Then the set S is equal to
(1) ϕ (an empty set)
(2) {0}
(3) {π}
(4) {0, π}
72. If the curves y2 = 6x, 9x2 + by2 = 16 intersect each other at right angles, then the value of b is
(1) 6
(2) 7/2
(3) 4
(4) 9/2
73. Let 
x ∈ R – {−1, 0, 1}. If 
then the local minimum value of h(X) is:
(1) 3
(2) −3
(3) −2√2
(4) 2√2
74. The integral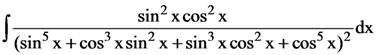 
is equal to
(1) 
(2) 
(3) 
(4) 
75. Then value of 
is :
(1) π/8
(2) π/2
(3) 4π
(4) π/4
76. Let g(x) = cos x2, f(x) = √x, and α, β (α < β) be the roots of the quadratic equation 18x2 – 9πx + π2 = 0. Then the area (in sq. units) bounded by the curve y = (gof) (x) and the lines x = α, x = β and y = 0 is
(1) 
(2) 
(3) 
(4) 
77. Let y = y(x) be the solution of the differential equation 
x ∈ (0, π. If 
then y(π/6) is equal to :
(1) 
(2) 
(3) 
(4) 
78. A straight line through a fixed point (2, 3) intersects the coordinate axes at distinct points P and Q. If O is the origin and the rectangle OPRQ is completed, then the locus of R is
(1) 3x + 2y = 6
(2) 2x + 3y = xy
(3) 3x + 2y = xy
(4) 3x + 2y = 6xy
79. Let the orthocentre and centroid of a triangle be A(–3, 5) and B(3, 3) respectively. If C is the circumcentre of this triangle, then the radius of the circle having line segment AC as diameter, is
(1) √10
(2) 2√10
(3) 
(4) 
80. If the tangent at (1, 7) to the curve x2 = y – 6 touches the circle x2 + y2 + 16x + 12y + c = 0 then the value of c is
(1) 195
(2) 185
(3) 85
(4) 95
81. Tangent and normal are drawn at P(16, 16) on the parabola y2 = 16x, which intersect the axis of the parabola at A and B, respectively. If C is the centre of the circle through the points P, A and B and ∠CPB = θ, then a value of tan θ is
(1) 1/2
(2) 2
(3) 3
(4) 4/3
82. Tangents are drawn to the hyperbola 4x2 – y2 = 36 at the points P and Q. If these tangents intersect at the point T(0, 3) then the area (in sq. units) of ∆PTQ is
(1) 45√5
(2) 54√3
(3) 60√3
(4) 36√5
83. If L1 is the the line of intersection of the planes 2x – 2y + 3z – 2 = 0, x – y + z + 1 = 0 and L2 is the line of intersection of the planes x + 2y – z – 3 = 0, 3x – y + 2z – 1 = 0, then the distance of the origin from the plane containing the lines L1 and L2, is
(1) 
(2) 
(3) 
(4) 
84. The length of the projection of the line segment joining the points (5, –1, 4) and (4, –1, 3) on the plane, x + y + z = 7 is:
(1) 2/√3
(2) 2/3
(3) 1/3
(4) 
85. Let 
be a vector coplanar with the vectors 
If is perpendicular to 
is equal to
(1) 336
(2) 315
(3) 256
(4) 84
86. A bag contains 4 red and 6 black balls. A ball is drawn at random from the bag, its colour is observed and this ball along with two additional balls of the same colour are returned to the bag. If now a ball is drawn at random from the bag, then the probability that this drawn ball is red, is:
(1) 3/10
(2) 2/5
(3) 1/5
(4) 3/4
87. If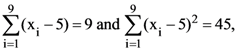 
then the standard deviation of the 9 items x1, x2, …. ., x9 is
(1) 9
(2) 4
(3) 2
(4) 3
88. If sum of all the solutions of the equation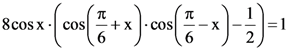 
in [0, π] is kπ, then k is equal to :
(1) 2/3
(2) 13/9
(3) 8/9
(4) 20/9
89. PQR is a triangular park with PQ = PR = 200 m. A T.V. tower stands at the mid-point of QR. If the angles of elevation of the top of the tower at P, Q and R are respectively 45º, 30º and 30º, then the height of the tower (in m) is
(1) 100
(2) 50
(3) 100√3
(4) 50√2
90. The Boolean expression ~ (p ⋁ q) ⋁ (~ p ⋀ q) is equivalent to
(1) ~p
(2) p
(3) q
(4) ~q
Latest Govt Job & Exam Updates: