JEE Main
All India JEE Main Cut-off for Top NITs in 2019
All India JEE Main Cut-off for Top NITs in 2019
Content
NIT Bhopal JEE Main Cutoff 2019……………………………1
NIT Calicut JEE Main Cutoff 2019……………………………2
NIT Jaipur JEE Main Cutoff 2019…………………………….3
NIT Allahabad JEE Main Cutoff 2019 ………………………4
NIT Tiruchirappalli JEE Main Cutoff 2019………………….5
NIT Bhopal JEE Main Cutoff 2019
| Course | CSE | ECE | ME |
| Gen (Male) | AIR – 7290 | AIR-12504 | AIR- 18418 |
| HSR – 8442 | HSR- 13274 | HSR- 20625 | |
| Gen (Female) |
AIR- 10640 | AIR- 16571 | AIR- 31634 |
| HSR- 12387 | HSR- 19572 | HSR- 38109 | |
| OBC (Male) | AIR- 2404 | AIR- 4410 | AIR- 6346 |
| HSR- 3079 | HSR- 5912 | HSR- 7858 | |
| OBC (Female) | AIR-4869 | AIR- 7219 | AIR- 12167 |
| HSR- 6890 | HSR- 9396 | HSR- 13405 | |
| EWS (Male) | AIR- 918 | AIR- 1654 | AIR- 2387 |
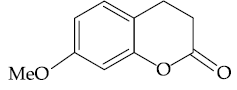
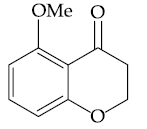
| HSR- 1089 | HSR- 1998 | HSR- 2724 | |
| EWS (Female) | AIR- 1577 | AIR- | AIR- 4801 |
| HSR- 1775 | HSR- 2802 | HSR- 5079 | |
| SC (Male) | AIR- 1581 | AIR- 2738 | AIR- 3622 |
| HSR- 1957 | HSR- 3861 | HSR- 5770 | |
| SC (Female) | AIR- 2191 | AIR- 4118 | AIR- 6783 |
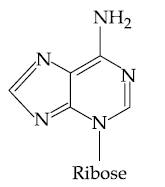
| HSR- 2919 | HSR- 4972 | HSR- 6689 | |
| ST (Male) | AIR- 813 | AIR- 1286 | AIR- 1431 |
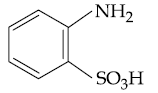
| HSR- 800 | HSR- 1886 | HSR- 2132 | |
| ST (Female) | AIR- 1279 | AIR- 2040 | AIR- 2294 |
| HSR- 1883 | HSR- 3373 | HSR- 4658 |
NIT Calicut JEE Main Cutoff 2019
| Course | CSE | ECE | ME |
| Gen (Male) | AIR- 4820 | AIR- 8378 | AIR- 13855 |
| HSR- 11022 | HSR- 17059 | HSR- 23778 | |
| Gen (Female) | AIR- 8265 | AIR- 11676 | AIR- 24443 |
| HSR- 16162 | HSR- 19452 | HSR- 31832 | |
| OBC (Male) | AIR- 1553 | AIR- 2366 | AIR- 4217 |
| HSR- 3542 | HSR- 4809 | HSR- 7658 | |
| OBC (Female) | AIR- 3705 | AIR- 4493 | AIR- 10465 |
| HSR- 6048 | HSR- 7361 | HSR- 11627 | |
| EWS (Male) | AIR- 632 | AIR- 995 | AIR- 1684 |
| HSR- 2970 | HSR- 4883 | HSR- 6647 | |
| EWS (Female) | AIR- 978 | AIR- 1450 | AIR- 3100 |
| HSR- 5567 | HSR- 9092 | HSR- 11064 | |
| SC (Male) | AIR- 739 | AIR- 1340 | AIR- 2129 |
| HSR- 1476 | HSR- 4960 | HSR- 9104 | |
| SC (Female) | AIR- 1452 | AIR- 2057 | AIR- 5001 |
| HSR- 5526 | HSR- 8101 | HSR- 13965 | |
| ST (Male) | AIR- 400 | AIR- 623 | AIR- 936 |
| HSR- 9136 | HSR- 13425 | HSR- 15912 | |
| ST (Female) | AIR- 759 | AIR- 981 | AIR- 1727 |
| HSR- 1897 | HSR- | HSR- |
NIT Jaipur JEE Main Cutoff 2019
| Course | CSE | ECE | ME |
| Gen (Male) | AIR- 4566 | AIR- 9208 | AIR- 14776 |
| HSR- 4483 | HSR- 8905 | HSR- 13541 | |
| Gen (Female) | AIR- 6169 | AIR- 14157 | AIR- 27774 |
| HSR- 6462 | HSR- 11612 | HSR- 22246 | |
| OBC (Male) | AIR- 1658 | AIR- 3529 | AIR- 4979 |
| HSR- 1721 | HSR- 3548 | HSR- 4769 | |
| OBC (Female) | AIR- 3605 | AIR- 6090 | AIR- 12086 |
| HSR- 4172 | HSR- 6438 | HSR- 8962 | |
| EWS (Male) | AIR- 576 | AIR- 1245 | AIR- 2034 |
| HSR- 607 | HSR- 1299 | HSR- 1765 | |
| EWS (Female) | AIR- 1485 | AIR- 2445 | AIR- 3851 |
| HSR- 1533 | HSR- 2487 | HSR- 4231 | |
| SC (Male) | AIR- 974 | AIR- 2184 | AIR- 3058 |
| HSR- 929 | HSR- 2026 | HSR- 2204 | |
| SC (Female) | AIR- 2874 | AIR- 3653 | AIR- 4162 |
| HSR- 1410 | HSR- 2160 | HSR- 4635 | |
| ST (Male) | AIR- 576 | AIR- 1170 | AIR- 1340 |
| HSR- 397 | HSR- 711 | HSR- 701 | |
| ST (Female) | AIR- 1007 | AIR- | AIR- 1719 |
| HSR- | HSR- 409 | HSR- 1793 |
NIT Allahabad JEE Main Cutoff 2019
| Course | CSE | ECE | ME |
| Gen (Male) | AIR- 3562 | AIR- 7402 | AIR- 13393 |
| HSR- 4714 | HSR- 8433 | HSR- 13139 | |
| Gen (Female) | AIR- 6198 | AIR- 11836 | AIR- 23254 |
| HSR- 8136 | HSR- 12716 | HSR- 26808 | |
| OBC (Male) | AIR- 1200 | AIR- 2785 | AIR- 4347 |
| HSR- 1538 | HSR- 2833 | HSR- 4212 | |
| OBC (Female) | AIR- 3630 | AIR- 5166 | AIR- 10551 |
| HSR- 3085 | HSR- 6112 | HSR- 12841 | |
| EWS (Male) | AIR- 434 | AIR- 841 | AIR- 1655 |
| HSR- 610 | HSR- 1061 | HSR- 1672 | |
| EWS (Female) | AIR- 1151 | AIR- 1544 | AIR- 4133 |
| HSR- 970 | HSR- 2033 | HSR- | |
| SC (Male) | AIR- 752 | AIR- 1931 | AIR- 2488 |
| HSR- 806 | HSR- 1639 | HSR- 2438 | |
| SC (Female) | AIR- 1350 | AIR- 2825 | AIR- 5904 |
| HSR- 2045 | HSR- 3855 | HSR- 4625 | |
| ST (Male) | AIR- 363 | AIR- 933 | AIR- 1013 |
| HSR- 779 | HSR- 1480 | HSR- 1819 | |
| ST (Female) | AIR- 707 | AIR- | AIR- 3254 |
| HSR- 1744 | HSR- 2482 | HSR- 4195 |
NIT Tiruchirappalli JEE Main Cutoff 2019
| Course | CSE | ECE | ME |
| Gen (Male) | AIR- 1373 | AIR- 3019 | AIR- 5968 |
| HSR- 5325 | HSR- 9158 | HSR- 14600 | |
| Gen (Female) | AIR- 2371 | AIR- 3508 | AIR- 12533 |
| HSR- 4075 | HSR- 11229 | HSR- 25415 | |
| OBC (Male) | AIR- 357 | AIR- 967 | AIR- 2178 |
| HSR- 2165 | HSR- 3010 | HSR- 4388 | |
| OBC (Female) | AIR- 1060 | AIR- 2577 | AIR- 4997 |
| HSR- 4085 | HSR- 5116 | HSR- 7108 | |
| EWS (Male) | AIR- 165 | AIR- 352 | AIR- 749 |
| HSR- 2058 | HSR- 13066 | HSR- 23632 | |
| EWS (Female) | AIR- 305 | AIR- 488 | AIR- 1849 |
| HSR- 2489 | HSR- 6613 | HSR- | |
| SC (Male) | AIR- 138 | AIR- 450 | AIR- 842 |
| HSR- 1300 | HSR- 2939 | HSR- 2933 | |
| SC (Female) | AIR- 420 | AIR- 1423 | AIR- 2280 |
| HSR- 1435 | HSR- 2711 | HSR- 7459 | |
| ST (Male) | AIR- 53 | AIR- 230 | AIR- 373 |
| HSR- 4708 | HSR- 5494 | HSR- 6978 | |
| ST (Female) | AIR- 59 | AIR- 321 | AIR- 1155 |
| HSR- 4295 | HSR- 2776 | HSR- |
JEE Main Online Computer Based Test (CBT) Examination Held on 16-04-2018 Morning Question Paper With Answer Key
JEE Main Online Computer Based Test (CBT) Examination Morning Held on 16-04-2018
Timing : 9 : 30 AM – 12 : 30 PM
1. The percentage errors in quantities P, Q, R and S are 0.5%, 1%, 3% and 1.5% respectively in the measurement of a physical quantity 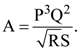 The maximum percentage error in the value of A will be :
The maximum percentage error in the value of A will be :
(1) 6.0%
(2) 7.5%
(3) 8.5%
(4) 6.5%
2. Let 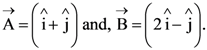 The magnitude of a coplanar vector
The magnitude of a coplanar vector ![]() such that
such that ![]() is given by :
is given by :
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
3. A body of mass m starts moving from rest along x-axis so that its velocity varies as ![]() where a is a constant and s is the distance covered by the body. The total work done by all the forces acting on the body in the first t seconds after the start of the motion is :
where a is a constant and s is the distance covered by the body. The total work done by all the forces acting on the body in the first t seconds after the start of the motion is :
(1) ![]()
(2) 8 m a4t2
(3) 4 m a4t2
(4) ![]()
4. Two particles of the same mass m are moving in circular orbits because of force, given by
![]()
The first particle is at a distance r=1, and the second, at r=4. The best estimate for the ratio of kinetic energies of the first and the second particle is closest to :
(1) 6 × 10−2
(2) 3 × 10−3
(3) 10−1
(4) 6 × 102
5. An oscillator of mass M is at rest in its equilibrium position in a potential ![]() A particle of mass m comes from right with speed u and collides completely inelastically with M and sticks to it. This process repeats every time the oscillator crosses its equilibrium position. The amplitude of oscillations after 13 collisions is : (M = 10, m = 5, u = 1, k = 1)
A particle of mass m comes from right with speed u and collides completely inelastically with M and sticks to it. This process repeats every time the oscillator crosses its equilibrium position. The amplitude of oscillations after 13 collisions is : (M = 10, m = 5, u = 1, k = 1)
(1) ![]()
(2) 1/2
(3) 2/3
(4) ![]()
6. Suppose that the angular velocity of rotation of earth is increased. Then, as a consequence :
(1) Weight of the object, everywhere on the earth, will increase.
(2) Weight of the object, everywhere on the earth, will decrease.
(3) There will be no change in weight anywhere on the earth.
(4) Except at poles, weight of the object on the earth will decrease.
7. A thin circular disk is in the xy plane as shown in the figure. The ratio of its moment of inertia about z and zʹ axes will be :
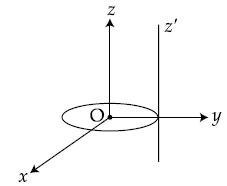
(1) 1 : 3
(2) 1 : 4
(3) 1 : 5
(4) 1 : 2
8. The relative uncertainty in the period of a satellite orbiting around the earth is 10−2. If the relative uncertainty in the radius of the orbit is negligible, the relative uncertainty in the mass of the earth is :
(1) 10−2
(2) 2 × 10−2
(3) 3 × 10−2
(4) 6 × 10−2
9. A small soap bubble of radius 4 cm is trapped inside another bubble of radius 6 cm without any contact. Let P2 be the pressure inside the inner bubble and P0, the pressure outside the outer bubble. Radius of another bubble with pressure difference P2 − P0 between its inside and outside would be :
(1) 12 cm
(2) 2.4 cm
(3) 6 cm
(4) 4.8 cm
10. One mole of an ideal monoatomic gas is taken along the path ABCA as shown in the PV diagram. The maximum temperature attained by the gas along the path BC is given by :
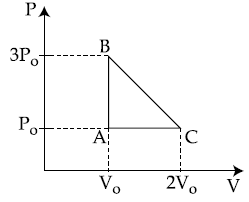
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
11. Two moles of helium are mixed with n moles of hydrogen. If  for the mixture, then the value of n is :
for the mixture, then the value of n is :
(1) 1
(2) 3
(3) 2
(4) 3/2
12. A particle executes simple harmonic motion and is located at x=a, b and c at times to, 2to and 3to The frequency of the oscillation is :
(1) 
(2) 
(3) 
(4) 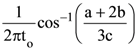
13. Two sitar strings, A and B, playing the note ‘Dha’ are slightly out of tune and produce beats of frequency 5 Hz. The tension of the string B is slightly increased and the beat frequency is found to decrease by 3 Hz. If the frequency of A is 425 Hz, the original frequency of B is :
(1) 430 Hz
(2) 420 Hz
(3) 428 Hz
(4) 422 Hz
14. Two identical conducting spheres A and B, carry equal charge. They are separated by a distance much larger than their diameters, and the force between them is F. A third identical conducting sphere, C, is uncharged. Sphere C is first touched to A, then to B, and then removed. As a result, the force between A and B would be equal to :
(1) F
(2) 3F/4
(3) 3F/8
(4) F/2
15. A heating element has a resistance of 100 Ω at room temperature. When it is connected to a supply of 220 V, a steady current of 2 A passes in it and temperature is 500°C more than room temperature. What is the temperature coefficient of resistance of the heating element ?
(1) 0.5 × 10−4 °C−1
(2) 5 × 10−4 °C−1
(3) 1 × 10−4 °C−1
(4) 2 × 10−4 °C−1
16. A galvanometer with its coil resistance 25 Ω requires a current of 1 mA for its full deflection. In order to construct an ammeter to read up to a current of 2 A, the approximate value of the shunt resistance should be :
(1) 2.5 × 10−3 Ω
(2) 1.25 × 10−2 Ω
(3) 1.25 × 10−3 Ω
(4) 2.5 × 10−2 Ω
17. In the following circuit, the switch S is closed at t=0. The charge on the capacitor C1 as a function of time will be given by 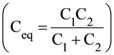
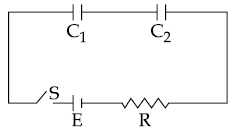
(1) C1E [1 − exp(−tR/C1)]
(2) C2E [1 − exp(−t/RC2)]
(3) CeqE [1 − exp(−t/RCeq)]
(4) CeqE exp (−t/RCeq)
18. A coil of cross-sectional area A having n turns is placed in a uniform magnetic field B. When it is rotated with an angular velocity ω, the maximum e.m.f. induced in the coil will be :
(1) 3 nBAω
(2) ![]()
(3) nBAω
(4) ![]()
19. A charge q is spread uniformly over an insulated loop of radius r. If it is rotated with an angular velocity ω with respect to normal axis then the magnetic moment of the loop is :
(1) q ωr2
(2) ![]()
(3) ![]()
(4) ![]()
20. A power transmission line feeds input power at 2300 V to a step down transformer with its primary windings having 4000 turns, giving the output power at 230 V. If the current in the primary of the transformer is 5 A, and its efficiency is 90%, the output current would be :
(1) 50 A
(2) 45 A
(3) 25 A
(4) 20 A
21. A plane electromagnetic wave of wavelength λ has an intensity I. It is propagating along the positive Y-direction. The allowed expressions for the electric and magnetic fields are given by :
(1) 
(2) 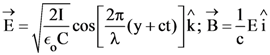
(3) 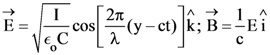
(4) 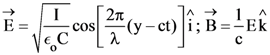
22. A ray of light is incident at an angle of 60° on one face of a prism of angle 30°. The emergent ray of light makes an angle of 30° with incident ray. The angle made by the emergent ray with second face of prism will be :
(1) 0°
(2) 90°
(3) 45°
(4) 30°
23. Unpolarized light of intensity I is incident on a system of two polarizers, A followed by B. The intensity of emergent light is I/2. If a third polarizer C is placed between A and B, the intensity of emergent light is reduced to I/3. The angle between the polarizers A and C is θ. Then :
(1) 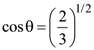
(2) 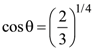
(3) 
(4) 
24. The de-Broglie wavelength (λB) associated with the electron orbiting in the second excited state of hydrogen atom is related to that in the ground state (λG) by :
(1) λB = 2λG
(2) λB = 3λG
(3) λB = λG/2
(4) λB = λG/3
25. Both the nucleus and the atom of some element are in their respective first excited states. They get de-excited by emitting photons of wavelengths λN, λA The ratio ![]() is closest to :
is closest to :
(1) 10−6
(2) 10
(3) 10−10
(4) 10−1
26. At some instant, a radioactive sample S1 having an activity 5 μCi has twice the number of nuclei as another sample S2 which has an activity of 10 μCi. The half lives of S1 and S2 are :
(1) 20 years and 5 years, respectively
(2) 20 years and 10 years, respectively
(3) 5 years and 20 years, respectively
(4) 10 years and 20 years, respectively
27. In the given circuit, the current through zener diode is :
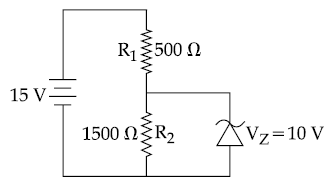
(1) 5.5 mA
(2) 6.7 mA
(3) 2.5 mA
(4) 3.3 mA
28. A carrier wave of peak voltage 14 V is used for transmitting a message signal. The peak voltage of modulating signal given to achieve a modulation index of 80% will be :
(1) 7 V
(2) 28 V
(3) 11.2 V
(4) 22.4 V
29. In a circuit for finding the resistance of a galvanometer by half deflection method, a 6 V battery and a high resistance of 11 kΩ are used. The figure of merit of the galvanometer is 60 μA/division. In the absence of shunt resistance, the galvanometer produces a deflection of θ = 9 divisions when current flows in the circuit. The value of the shunt resistance that can cause the deflection of θ/2, is closest to :
(1) 550 Ω
(2) 220Ω
(3) 55Ω
(4) 110Ω
30. The end correction of a resonance column is 1 cm. If the shortest length resonating with the tuning fork is 10 cm, the next resonating length should be :
(1) 28 cm
(2) 32 cm
(3) 36 cm
(4) 40 cm
31. An unknown chlorohydrocarbon has 3.55% of chlorine. If each molecule of the hydrocarbon has one chlorine atom only; chlorine atoms present in 1 g of chlorohydrocarbon are :
(Atomic wt. of Cl=35.5 u; Avogadro constant=6.023 × 1023 mol−1)
(1) 6.023 × 1020
(2) 6.023 × 109
(3) 6.023 × 1021
(4) 6.023 × 1023
32. The gas phase reaction 2NO2(g) → N2O4(g) is an exothermic reaction. The decomposition of N2O4, in equilibrium mixture of NO2(g) and N2O4(g), can be increased by :
(1) lowering the temperature.
(2) increasing the pressure.
(3) addition of an inert gas at constant volume.
(4) addition of an inert gas at constant pressure.
33. Assuming ideal gas behaviour, the ratio of density of ammonia to that of hydrogen chloride at same temperature and pressure is : (Atomic wt. of Cl=35.5 u)
(1) 1.46
(2) 0.46
(3) 1.64
(4) 0.64
34. When 9.65 ampere current was passed for 1.0 hour into nitrobenzene in acidic medium, the amount of p-aminophenol produced is :
(1) 9.81 g
(2) 10.9 g
(3) 98.1 g
(4) 109.0 g
35. For which of the following processes, ΔS is negative ?
(1) H2(g) → 2H(g)
(2) N2(g, 1 atm) → N2(g, 5 atm)
(3) C(diamond) → C(graphite)
(4) N2(g, 273 K) → N2(g, 300 K)
36. Which one of the following is not a property of physical adsorption ?
(1) Higher the pressure, more the adsorption
(2) Lower the temperature, more the adsorption
(3) Greater the surface area, more the adsorption
(4) Unilayer adsorption occurs
37. If 50% of a reaction occurs in 100 second and 75% of the reaction occurs in 200 second, the order of this reaction is :
(1) Zero
(2) 1
(3) 2
(4) 3
38. Which of the following statements is false ?
(1) Photon has momentum as well as wavelength.
(2) Splitting of spectral lines in electrical field is called Stark effect.
(3) Rydberg constant has unit of energy.
(4) Frequency of emitted radiation from a black body goes from a lower wavelength to higher wavelength as the temperature increases.
39. At 320 K, a gas A2 is 20% dissociated to A(g). The standard free energy change at 320 K and 1 atm in J mol−1 is approximately : (R=8.314 JK−1 mol−1; ln 2=0.693; ln 3=1.098)
(1) 4763
(2) 2068
(3) 1844
(4) 4281
40. The mass of a non-volatile, non-electrolyte solute (molar mass=50 g mol−1) needed to be dissolved in 114 g octane to reduce its vapour pressure to 75%, is :
(1) 37.5 g
(2) 75 g
(3) 150 g
(4) 50 g
41. The incorrect statement is :
(1) Cu2+ salts give red coloured borax bead test in reducing flame.
(2) Cu2+ and Ni2+ ions give black precipitate with H2S in presence of HCl solution.
(3) Ferricion gives blood red colour with potassium thiocyanate.
(4) Cu2+ ion gives chocolage coloured precipitate with potassium ferrocyanide solution.
42. The incorrect geometry is represented by :
(1) BF3 – trigonal planar
(2) H2O – bent
(3) NF3 – trigonal planar
(4) AsF5 – trigonal bipyramidal
43. In Wilkinson’s catalyst, the hybridization of central metal ion and its shape are respectively :
(1) sp3d, trigonal bipyramidal
(2) sp3, tetrahedral
(3) dsp2, square planar
(4) d2sp3, octahedral
44. Among the oxides of nitrogen : N2O3, N2O4 and N2O5 ; the molecule(s) having nitrogen-nitrogen bond is/are :
(1) Only N2O5
(2) N2O3 and N2O5
(3) N2O4 and N2O5
(4) N2O3 and N2O4
45. Which of the following complexes will show geometrical isomerism ?
(1) aquachlorobis(ethylenediamine) cobalt(II) chloride
(2) pentaaquachlorochromium(III) chloride
(3) potassium amminetrichloroplatinate (II)
(4) potassium tris(oxalato)chromate(III)
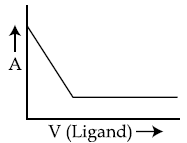
46. In a complexometric titration of metal ion with ligand M(Metal ion)+L(Ligand) → C(Complex) end point is estimated spectrophotometrically (through light absorption). If ‘M’ and ‘C’ do not absorb light and only ‘L’ absorbs, then the titration plot between absorbed light (A) versus volume of ligand ‘L’ (V) would look like :
(1) 
(2) 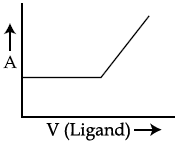
(3) 
(4) 
47. In the extraction of copper from its sulphide ore, metal is finally obtained by the oxidation of cuprous sulphide with :
(1) Fe2O3
(2) Cu2O
(3) SO2
(4) CO
48. Which of the following conversions involves change in both shape and hybridisation ?
(1) NH3 → NH4+
(2) CH4 → C2H6
(3) H2O → H3O+
(4) BF3 → BF4−
49. A group 13 element ‘X’ reacts with chlorine gas to produce a compound XCl3 . XCl3 is electron deficient and easily reacts with NH3 to form Cl3X ← NH3 adduct; however, XCl3 does not dimerize. X is :
(1) B
(2) Al
(3) Ga
(4) In
50. When XO2 is fused with an alkali metal hydroxide in presence of an oxidizing agent such as KNO3 ; a dark green product is formed which disproportionates in acidic solution to afford a dark purple solution. X is :
(1) Ti
(2) V
(3) Cr
(4) Mn
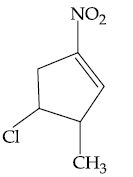
51. The major product of the following reaction is :

(1) 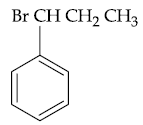
(2) 
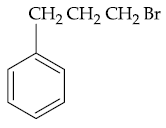
(3) 
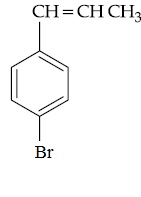
(4) 
52. For standardizing NaOH solution, which of the following is used as a primary standard ?
(1) Ferrous Ammonium Sulfate
(2) dil. HCl
(3) Oxalic acid
(4) Sodium tetraborate
53. The most polar compound among the following is :
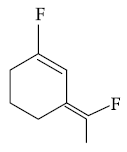
(1) 
(2) 
(3) 
(4) 
54. The correct match between items of List – I and List – II is :

(1) (A)-(R), (B)-(S), (C)-(P), (D)-(Q)
(2) (A)-(S), (B)-(R), (C)-(P), (D)-(Q)
(3) (A)-(S), (B)-(R), (C)-(Q), (D)-(P)
(4) (A)-(R), (B)-(S), (C)-(Q), (D)-(P)
55. Among the following, the incorrect statement is :
(1) Maltose and lactose has 1, 4-glycosidic linkage.
(2) Sucrose and amylose has 1, 2-glycosidic linkage.
(3) Cellulose and amylose has 1, 4-glycosidic linkage.
(4) Lactose contains β-D-galactose and β-D-glucose.
56. Which of the following compounds will most readily be dehydrated to give alkene under acidic condition ?
(1) 1-Pentanol
(2) 4-Hydroxypentan-2-one
(3) 3-Hydroxypentan-2-one
(4) 2-Hydroxycyclopentanone
57. Products A and B formed in the following reactions are respectively :
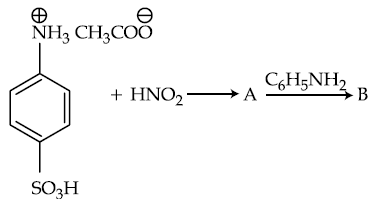
(1) 
(2) 
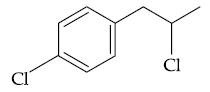
(3) 
(4) 
58. The major product B formed in the following reaction sequence is :

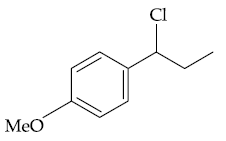
(1) 
(2) 
(3) 
(4) 
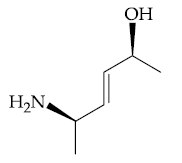
59. The major product of the following reaction is :

(1) 
(2) 
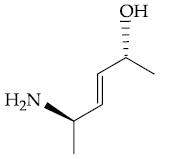
(3) 
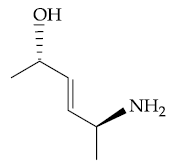
(4) 
60. The major product of the following reaction is :

(1) 
(2) 
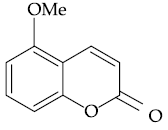
(3) 
(4) 
61. Let N denote the set of all natural numbers. Define two binary relations on N as R1={(x, y) ϵ N × N : 2x + y = 10} and R2={(x, y) ϵ N × N : x + 2y = 10}. Then :
(1) Range of R1 is {2, 4, 8}.
(2) Range of R2 is {1, 2, 3, 4}.
(3) Both R1 and R2 are symmetric relations.
(4) Both R1 and R2 are transitive relations.
62. Let p, q and r be real numbers (p ≠ q, r ≠ 0), such that the roots of the equation ![]() are equal in magnitude but opposite in sign, then the sum of squares of these roots is equal to :
are equal in magnitude but opposite in sign, then the sum of squares of these roots is equal to :
(1) 
(2) p2 + q2
(3) 2(p2 + q2)
(4) p2 + q2 + r2
63. The least positive integer n for which  is
is
(1) 2
(2) 3
(3) 5
(4) 6
64. Let  and B = A20. Then the sum of the elements of the first column of B is :
and B = A20. Then the sum of the elements of the first column of B is :
(1) 210
(2) 211
(3) 231
(4) 251
65. The number of values of k for which the system of linear equations,
(k + 2)x + 10y = k
kx + (k + 3)y = k – 1
has no solution, is :
(1) 1
(2) 2
(3) 3
(4) infinitely many
66. The number of numbers between 2,000 and 5,000 that can be formed with the digits 0, 1, 2, 3, 4 (repetition of digits is not allowed) and are multiple of 3 is :
(1) 24
(2) 30
(3) 36
(4) 48
67. The coefficient of x2 in the expansion of the product (2− x2) ⋅ ((1 + 2x + 3x2)6+ (1 − 4x2)6) is :
(1) 107
(2) 106
(3) 108
(4) 155
68. Let 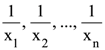 (xi ≠ 2 for i = 1, 2, . . . , n) be in A.P. such that x1 = 4 and x21 = 20. If n is the least positive integer for which xn > 50, then
(xi ≠ 2 for i = 1, 2, . . . , n) be in A.P. such that x1 = 4 and x21 = 20. If n is the least positive integer for which xn > 50, then 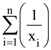 is equal to :
is equal to :
(1) 1/8
(2) 3
(3) 13/8
(4) 13/4
69. The sum of the first 20 terms of the series ![]() is :
is :
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
70. 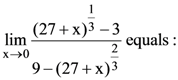
(1) 1/3
(2) −1/3
(3) −1/6
(4) 1/6
71. If the function f defined as ![]() is continuous at x = 0, then the ordered pair (k, f(0)) is equal to :
is continuous at x = 0, then the ordered pair (k, f(0)) is equal to :
(1) (3, 2)
(2) (3, 1)
(3) (2, 1)
(4) (1/3, 2)
72. If ![]() then
then ![]() is equal to :
is equal to :
(1) y/x
(2) x/y
(3) −y/x
(4) −x/y
73. Let M and m be respectively the absolute maximum and the absolute minimum values of the function, f (x)=2x3 − 9x2 + 12x + 5 in the interval [0, 3]. Then M−m is equal to :
(1) 5
(2) 9
(3) 4
(4) 1
74. If ![]()
![]() (C is a constant of integration), then the ordered pair (K, A) is equal to :
(C is a constant of integration), then the ordered pair (K, A) is equal to :
(1) (2, 1)
(2) (−2, 3)
(3) (2, 3)
(4) (−2, 1)
75. If ![]() then :
then :
(1) fʹʹʹ(x) + fʹʹ(x) = sin x
(2) fʹʹʹ(x) + fʹʹ(x) – fʹ(x) = cos x
(3) fʹʹʹ(x) + fʹ(x) = cos x – 2x sin x
(4) fʹʹʹ(x) – fʹʹ(x) = cos x – 2x sin x
76. If the area of the region bounded by the curves, y = x2, y = 1/x and the lines y = 0 and x = t (t > 1) is 1 sq. unit, then it is equal to :
(1) e3/2
(2) 4/3
(3) 3/2
(4) e2/3
77. The differential equation representing the family of ellipses having foci either on the x-axis or on the y-axis, centre at the origin and passing through the point (0, 3) is :
(1) xy yʹʹ + x(yʹ)2 – y yʹ = 0
(2) x + y yʹʹ = 0
(3) xy yʹ + y2 – 9 = 0
(4) xy yʹ – y2 + 9 = 0
78. The locus of the point of intersection of the lines, ![]() and
and ![]() (k is any non-zero real parameter), is :
(k is any non-zero real parameter), is :
(1) an ellipse whose eccentricity is 1/√3.
(2) an ellipse with length of its major axis 8√2.
(3) a hyperbola whose eccentricity is √3.
(4) a hyperbola with length of its transverse axis 8√2.
79. If a circle C, whose radius is 3, touches externally the circle, x2 + y2 + 2x − 4y – 4 = 0 at the point (2, 2), then the length of the intercept cut by this circle C, on the x-axis is equal to :
(1) 2√5
(2) 3√2
(3) √5
(4) 2√3
80. Let P be a point on the parabola, x2 = 4y. If the distance of P from the centre of the circle, x2 + y2 + 6x + 8 = 0 is minimum, then the equation of the tangent to the parabola at P, is :
(1) x + 4y – 2 = 0
(2) x – y + 3 = 0
(3) x + y + 1 = 0
(4) x + 2y = 0
81. If the length of the latus rectum of an ellipse is 4 units and the distance between a focus and its nearest vertex on the major axis is 3/2 units, then its eccentricity is :
(1) 1/2
(2) 1/3
(3) 2/3
(4) 1/9
82. The sum of the intercepts on the coordinate axes of the plane passing through the point (−2, −2, 2) and containing the line joining the points (1, −1, 2) and (1, 1, 1), is :
(1) 4
(2) −4
(3) −8
(4) 12
83. If the angle between the lines, ![]() is then p is
is then p is ![]() equal to :
equal to :
(1) 7/2
(2) 2/7
(3) −7/4
(4) −4/7
84. Let ![]() and a vector
and a vector ![]() be such that
be such that ![]() Then
Then ![]() equals :
equals :
(1) 11/3
(2) 11/√3
(3) ![]()
(4) ![]()
85. The mean and the standard deviation(s.d.) of five observations are 9 and 0, respectively. If one of the observations is changed such that the mean of the new set of five observations becomes 10, then their s.d. is :
(1) 0
(2) 1
(3) 2
(4) 4
86. Let A, B and C be three events, which are pair-wise independent and ![]() denotes the complement of an event E. If P(A ∩ B ∩ C) = 0 and P(C) > 0, then
denotes the complement of an event E. If P(A ∩ B ∩ C) = 0 and P(C) > 0, then ![]() is equal to :
is equal to :
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
87. Two different families A and B are blessed with equal number of children. There are 3 tickets to be distributed amongst the children of these families so that no child gets more than one ticket. If the probability that all the tickets go to the children of the family B is 1/12, then the number of children in each family is :
(1) 3
(2) 4
(3) 5
(4) 6
88. If an angle A of a ΔABC satisfies 5 cosA+3=0, then the roots of the quadratic equation, 9x2 + 27x + 20=0 are :
(1) sec A, cot A
(2) sin A, sec A
(3) sec A, tan A
(4) tan A, cos A
89. A man on the top of a vertical tower observes a car moving at a uniform speed towards the tower on a horizontal road. If it takes 18 min. for the angle of depression of the car to change from 30° to 45° ; then after this, the time taken (in min.) by the car to reach the foot of the tower, is :
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
90. If p→(∼p∨∼q) is false, then the truth values of p and q are respectively :
(1) F, F
(2) T, F
(3) F, T
(4) T, T
JEE Main Online Computer Based Test (CBT) Examination Held on 15-04-2018 Afternoon Question Paper With Answer Key
JEE Main Online Computer Based Test (CBT) Examination Afternoon Held on 15-04-2018,
PHYSICS
1. The characteristic distance at which quantum gravitational effects are significant, the Planck length, can be determined from a suitable combination of the fundamental physical constants G, h and c. Which of the following correctly gives the Planck length ?
(1) G h2 c3
(2) G2 h c
(3) G1/2 h2 c
(4) 
2. A man in a car at location Q on a straight highway is moving with speed υ. He decides to reach a point P in a field at a distance d from the highway (point M) as shown in the figure. Speed of the car in the field is half to that on the highway. What should be the distance RM, so that the time taken to reach P is minimum ?

(1) d
(2) d/√2
(3) d/2
(4) d/√3
3. A body of mass 2 kg slides down with an acceleration of 3 m/s2 on a rough inclined plane having a slope of 30°. The external force required to take the same body up the plane with the same acceleration will be : (g=10 m/s2)
(1) 14 N
(2) 20 N
(3) 6 N
(4) 4 N
4. A proton of mass m collides elastically with a particle of unknown mass at rest. After the collision, the proton and the unknown particle are seen moving at an angle of 90° with respect to each other. The mass of unknown particle is :
(1) m/2
(2) m
(3) m/√3
(4) 2 m
5. A disc rotates about its axis of symmetry in a horizontal plane at a steady rate of 3.5 revolutions per second. A coin placed at a distance of 1.25 cm from the axis of rotation remains at rest on the disc. The coefficient of friction between the coin and the disc is : (g=10 m/s2)
(1) 0.5
(2) 0.3
(3) 0.7
(4) 0.6
6. A thin uniform bar of length L and mass 8 m lies on a smooth horizontal table. Two point masses m and 2 m are moving in the same horizontal plane from opposite sides of the bar with speeds 2υ and υ respectively. The masses stick to the bar after collision at a distance ![]() respectively from the centre of the abr. If the bar starts rotating about its center of mass as a result of collision, the angular speed of the bar will be :
respectively from the centre of the abr. If the bar starts rotating about its center of mass as a result of collision, the angular speed of the bar will be :

(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
7. A thin rod MN, free to rotate in the vertical plane about the fixed end N, is held horizontal. When the end M is released the speed of this end, when the rod makes an angle α with the horizontal, will be proportional to : (see figure)
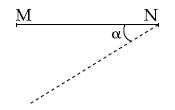
(1) ![]()
(2) sin α
(3) ![]()
(4) cos α
8. As shown in the figure, forces of 105 N each are applied in opposite directions, on the upper and lower faces of a cube of side 10 cm, shifting the upper face parallel to itself by 0.5 cm. If the side of another cube of the same material is 20 cm, then under similar conditions as above, the displacement will be :

(1) 0.25 cm
(2) 0.37 cm
(3) 0.75 cm
(4) 1.00 cm
9. When an air bubble of radius r rises from the bottom to the surface of a lake, its radius becomes 5r/4. Taking the atmospheric pressure to be equal to 10 m height of water column, the depth of the lake would approximately be (ignore the surface tension and the effect of temperature) :
(1) 11.2 m
(2) 8.7 m
(3) 9.5 m
(4) 10.5 m
10. Two Carnot engines A and B are operated in series. Engine A receives heat from a reservoir at 600 K and rejects heat to a reservoir at temperature T. Engine B receives heat rejected by engine A and in turn rejects it to a reservoir at 100 K. If the efficiencies of the two engines A and B are represented by ηA and ηB, respectively, then what is the value of ![]()
(1) 12/7
(2) 7/12
(3) 12/5
(4) 5/12
11. The value closest to the thermal velocity of a Helium atom at room temperature (300 K) in ms−1 : [kB = 1.4 × 10−23 J/K; mHe = 7 × 10−27 kg]
(1) 1.3 × 104
(2) 1.3 × 103
(3) 1.3× 105
(4) 1.3 × 102
12. Two simple harmonic motions, as shown below, are at right angles. They are combined to form Lissajous figures.
x(t) = A sin (at + δ)
y(t) = B sin (bt)
Identify the correct match below.
Parameters Curve
(1) A ≠ B, a = b ; δ = 0 Parabola
(2) A = B, a = b ; δ = π/2 Line
(3) A ≠ B, a = b ; δ = π/2 Ellipse
(4) A = B, a = 2b ; δ = π/2 Circle
13. 5 beats/second are heard when a tuning fork is sounded with a sonometer wire under tension, when the length of the sonometer wire is either 0.95 m or 1 m. The frequency of the fork will be :
(1) 195 Hz
(2) 150 Hz
(3) 300 Hz
(4) 251 Hz
14. A solid ball of radius R has a charge density ρ given by ρ = ρ0(1 – r/R) for 0 ≤ r ≤ The electric field outside the ball is :
(1) ![]()
(2) 
(3) 
(4) 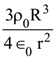
15. A parallel plate capacitor with area 200 cm2 and separation between the plates 1.5 cm, is connected across a battery of emf V. If the force of attraction between the plates is 25×10−6 N, the value of V is approximately :
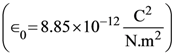
(1) 250 V
(2) 100 V
(3) 300 V
(4) 150 V
16. A copper rod of cross-sectional area A carries a uniform current I through it. At temperature T, if the volume charge density of the rod is ρ, how long will the charges take to travel a distance d ?
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
17. A capacitor C1=1.0 μF is charged up to a voltage V=60 V by connecting it to battery B through switch (1). Now C1 is disconnected from battery and connected to a circuit consisting of two uncharged capacitors C2=3.0 μF and C3=6.0 μF through switch (2), as shown in the figure. The sum of final charges on C2 and C3 is :

(1) 40 μC
(2) 36 μC
(3) 20 μC
(4) 54 μC
18. A current of 1 A is flowing on the sides of an equilateral triangle of side 4.5×10−2 The magnetic field at the centre of the triangle will be :
(1) 2 ×10−5 Wb/m2
(2) Zero
(3) 8 ×10−5 Wb/m2
(4) 4 ×10−5 Wb/m2
19. At the centre of a fixed large circular coil of radius R, a much smaller circular coil of radius r is placed. The two coils are concentric and are in the same The larger coil carries a current I. The smaller coil is set to rotate with a constant angular velocity ω about an axis along their common diameter. Calculate the emf induced in the smaller coil after a time t of its start of rotation.
(1) 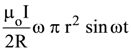
(2) 
(3) 
(4) 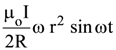
20. 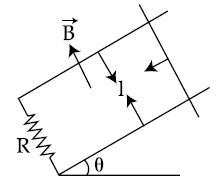
A copper rod of mass m slides under gravity on two smooth parallel rails, with
separation l and set at an angle of θ with the horizontal. At the bottom, rails are joined by a resistance R. There is a uniform magnetic field B normal to the plane of the rails, as shown in the figure. The terminal speed of the copper rod is :
(1) 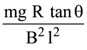
(2) 
(3) 
(4) 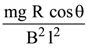
21. A plane polarized monochromatic EM wave is traveling in vacuum along z direction such that at t = t1 it is found that the electric field is zero at a spatial point z1. The next zero that occurs in its neighbourhood is at z2. The frequency of the electromagnetic wave is :
(1) 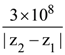
(2) 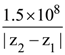
(3) 
(4) 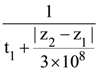
22. A convergent doublet of separated lenses, corrected for spherical aberration, has resultant focal length of 10 cm. The separation between the two lenses is 2 cm. The focal lengths of the component lenses are :
(1) 10 cm, 12 cm
(2) 12 cm, 14 cm
(3) 16 cm, 18 cm
(4) 18 cm, 20 cm
23. A plane polarized light is incident on a polariser with its pass axis making angle θ with x-axis, as shown in the figure. At four different values of θ, θ=8°, 38°, 188° and 218°, the observed intensities are same. What is the angle between the direction of polarization and x-axis ?

(1) 98°
(2) 128°
(3) 203°
(4) 45°
24. If the de Broglie wavelengths associated with a proton and an α-particle are equal, then the ratio of velocities of the proton and the α-particle will be :
(1) 4 : 1
(2) 2 : 1
(3) 1 : 2
(4) 1 : 4
25. Muon (μ−) is a negatively charged (|q| = |e|) particle with a mass mμ=200 me, where me is the mass of the electron and e is the electronic charge. If μ− is bound to a proton to form a hydrogen like atom, identify the correct statements.
(A) Radius of the muonic orbit is 200 times smaller than that of the electron.
(B) The speed of the μ− in the nth orbit is 1/200 times that of the electron in the nth orbit.
(C) The ionization energy of muonic atom is 200 times more than that of an hydrogen atom.
(D) The momentum of the muon in the nth orbit is 200 times more than that of the electron.
(1) (A), (B), (D)
(2) (A), (C), (D)
(3) (B), (D)
(4) (C), (D)
26. An unstable heavy nucleus at rest breaks into two nuclei which move away with velocities in the ratio of 8 : 27. The ratio of the radii of the nuclei (assumed to be spherical) is :
(1) 8 : 27
(2) 4 : 9
(3) 3 : 2
(4) 2 : 3
27. Truth table for the following digital circuit will be :
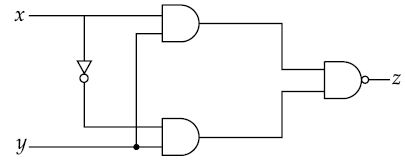
(1) 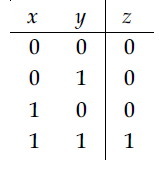
(2) 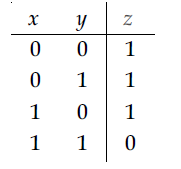
(3) 
(4) 
28. The carrier frequency of a transmitter is provided by a tank circuit of a coil of inductance 49 μH and a capacitance of 2.5 nF. It is modulated by an audio signal of 12 kHz. The frequency range occupied by the side bands is :
(1) 13482 kHz − 13494 kHz
(2) 442 kHz − 466 kHz
(3) 63 kHz − 75 kHz
(4) 18 kHz − 30 kHz
29. A constant voltage is applied between two ends of a metallic wire. If the length is halved and the radius of the wire is doubled, the rate of heat developed in the wire will be :
(1) Doubled
(2) Halved
(3) Unchanged
(4) Increased 8 times
30. A body takes 10 minutes to cool from 60°C to 50° The temperature of surroundings is constant at 25°C. Then, the temperature of the body after next 10 minutes will be approximately :
(1) 47°C
(2) 41°C
(3) 45°C
(4) 43°C
31. For per gram of reactant, the maximum quantity of N2 gas is produced in which of the following thermal decomposition reactions ?
(Given : Atomic wt. – Cr = 52 u, Ba = 137 u)
(1) (NH4)2Cr2O7(s) → N2(g)+4H2O(g) +Cr2O3(s)
(2) 2NH4NO3(s) → 2 N2(g)+4H2O(g) +O2(g)
(3) Ba(N3)2(s) → Ba(s)+3N2(g)
(4) 2NH3(g) → N2(g)+3H2(g)
32. All of the following share the same crystal structure except :
(1) LiCl
(2) NaCl
(3) RbCl
(4) CsCl
33. The de-Broglie’s wavelength of electron present in first Bohr orbit of ‘H’ atom is :
(1) 0529 Å
(2) 2π × 0.529 Å
(3) ![]()
(4) 4 × 0.529 Å
34. ∆fG° at 500 K for substance ‘S’ in liquid state and gaseous state are +100.7 kcal mol−1 and +103 kcal mol−1, respectively. Vapour pressure of liquid ‘S’ at 500 K is approximately equal to :
(R – 2 cal K−1 mol−1)
(1) 0.1 atm
(2) 1 atm
(3) 10 atm
(4) 100 atm
35. Given
(i) 2Fe2O3(s) → 4Fe(s)+3O2(g) ∆rG° = +1487.0 kJ mol−1
(ii) 2CO(g) + O2(g) → 2CO2(g); ∆rG° = −514.4 kJ mol−1
Free energy change, ∆rG° for the reaction 2Fe2O3(s) + 6CO(g) → 4Fe(s) + 6CO2(g) will be :
(1) −112.4 kJ mol−1
(2) −56.2 kJ mol−1
(3) −168.2 kJ mol−1
(4) −208.0 kJ mol−1
36. Two 5 molal solutions are prepared by dissolving a non-electrolyte non-volatile solute separately in the solvents X and Y. The molecular weights of the solvents are MX and MY, respectively where ![]() The relative lowering of vapour pressure of the solution in X is “m” times that of the solution in Y. Given that the number of moles of solute is very small in comparison to that of solvent, the value of “m” is :
The relative lowering of vapour pressure of the solution in X is “m” times that of the solution in Y. Given that the number of moles of solute is very small in comparison to that of solvent, the value of “m” is :
(1) 4/3
(2) 3/4
(3) 1/2
(4) 1/4
37. Following four solutions are prepared by mixing different volumes of NaOH and HCl of different concentrations, pH of which one of them will be equal to 1 ?
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
38. At a certain temperature in a 5 L vessel, 2 moles of carbon monoxide and 3 moles of chlorine were allowed to reach equilibrium according to the reaction,
CO + Cl2 ⇌ COCl2
At equilibrium, if one mole of CO is present then equilibrium constant (Kc) for the reaction is :
(1) 2
(2) 2.5
(3) 3
(4) 4
39. If x gram of gas is adsorbed by m gram of adsorbent at pressure P, the plot of ![]() versus log P is linear. The slope of the plot is :
versus log P is linear. The slope of the plot is :
(n and k are constants and n > 1)
(1) 2 k
(2) log k
(3) n
(4) 1/n
40. For a first order reaction, A → P, t1/2 (half-life) is 10 days. The time required for 1/4th conversion of A (in days) is :
(ln 2 = 0.693, ln 3 = 1.1)
(1) 5
(2) 3.2
(3) 4.1
(4) 2.5
41. Which of the following best describes the diagram below of a molecular orbital ?
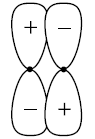
(1) A non-bonding orbital
(2) An antibonding σ orbital
(3) A bonding π orbital
(4) An antibonding π orbital
42. Biochemical Oxygen Demand (BOD) value can be a measure of water pollution caused by the organic matter. Which of the following statements is correct ?
(1) Aerobic bacteria decrease the BOD value.
(2) Anaerobic bacteria increase the BOD value.
(3) Clean water has BOD value higher than 10 ppm.
(4) Polluted water has BOD value higher than 10 ppm.
43. In KO2, the nature of oxygen species and the oxidation state of oxygen atom are, respectively :
(1) Oxide and −2
(2) Superoxide and −1/2
(3) Peroxide and −1/2
(4) Superoxide and −1
44. The number of P−O bonds in P4O6 is :
(1) 6
(2) 9
(3) 12
(4) 18
45. Lithium aluminium hydride reacts with silicon tetrachloride to form :
(1) LiCl, AlH3 and SiH4
(2) LiCl, AlCl3 and SiH4
(3) LiH, AlCl3 and SiCl2
(4) LiH, AlH3 and SiH4
46. The correct order of spin-only magnetic moments among the following is :
(Atomic number : Mn=25, Co=27, Ni=28, Zn=30)
(1) [ZnCl4]2− > [NiCl4]2− > [CoCl4]2− > [MnCl4]2−
(2) [CoCl4]2− > [MnCl4]2− > [NiCl4]2− > [ZnCl4]2−
(3) [NiCl4]2− > [CoCl4]2− > [MnCl4]2− > [ZnCl4]2−
(4) [MnCl4]2− > [CoCl4]2− > [NiCl4]2− > [ZnCl4]2−
47. The correct order of electron affinity is :
(1) F > Cl > O
(2) F > O > Cl
(3) Cl > F > O
(4) O > F > Cl
48. In XeO3F2, the number of bond pair(s), π-bond(s) and lone pair(s) on Xe atom respectively are :
(1) 5, 2, 0
(2) 4, 2, 2
(3) 5, 3, 0
(4) 4, 4, 0
49. In the leaching method, bauxite ore is digested with a concentrated solution of NaOH that produces ‘X’. When CO2 gas is passed through the aqueous solution of ‘X’, a hydrated compound ‘Y’ is precipitated. ‘X’ and ‘Y’ respectively are :
(1) NaAlO2 and Al2(CO3)3⋅ x H2O
(2) Al(OH)3 and Al2O3⋅ x H2O
(3) Na[Al(OH)4] and Al2O3⋅ x H2O
(4) Na[Al(OH)4] and Al2(CO3)3⋅ x H2O
50. The total number of possible isomers for square-planar [Pt(Cl)(NO2)(NO3)(SCN)]2− is :
(1) 8
(2) 12
(3) 16
(4) 24
51. Two compounds I and II are eluted by column chromatography (adsorption of I > II). Which one of following is a correct statement ?
(1) I moves faster and has higher Rf value than II
(2) II moves faster and has higher Rf value than I
(3) I moves slower and has higher Rf value than II
(4) II moves slower and has higher Rf value than I
52. Which of the following statements is not true ?
(1) Step growth polymerisation requires a bifunctional monomer.
(2) Nylon 6 is an example of step growth polymerisation.
(3) Chain growth polymerization includes both homopolymerisation and copolymerisation.
(4) Chain growth polymerization involves homopolymerisation only.
53. When 2-butyne is treated with H2/ Lindlar’s catalyst, compound X is produced as the major product and when treated with Na/liq. NH3 it produces Y as the major product. Which of the following statements is correct ?
(1) X will have higher dipole moment and higher boiling point than Y.
(2) Y will have higher dipole moment and higher boiling point than X.
(3) X will have lower dipole moment and lower boiling point than Y.
(4) Y will have higher dipole moment and lower boiling point than X.
54. The increasing order of the acidity of the following carboxylic acids is :
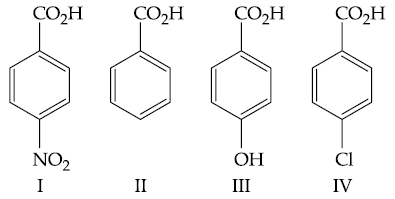
(1) I < III < II < IV
(2) IV < II < III < I
(3) II < IV < III < I
(4) III < II < IV < I
55. The major product formed in the following reaction is :

(1) 
(2) 
(3) 
(4) 
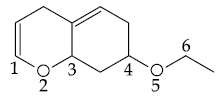
56. On treatment of the following compound with a strong acid, the most susceptible site for bond cleavage is :
(1) C1 – O2
(2) O2 – C3
(3) C4 – O5
(4) O5 – C6
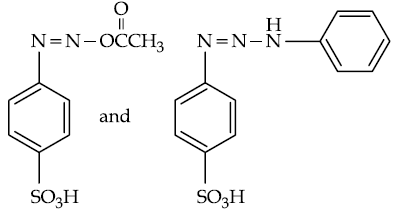
57. The increasing order of diazotisation of the following compounds is :


(1) (a) < (b) < (c) < (d)
(2) (a) < (d) < (b) < (c)
(3) (a) < (d) < (c) < (b)
(4) (d) < (c) < (b) < (a)
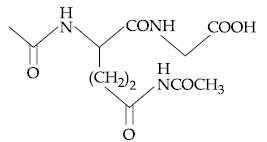
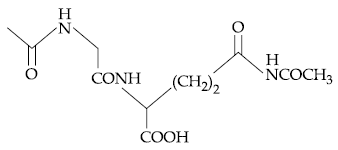
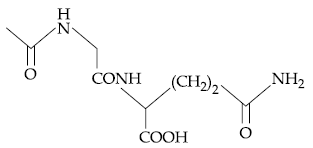
58. The dipeptide, Gln-Gly, on treatment with CH3COCl followed by aqueous work up gives :
(1) 
(2) 
(3) 
(4) 
59. The total number of optically active compounds formed in the following reaction is :

(1) Two
(2) Four
(3) Six
(4) Zero
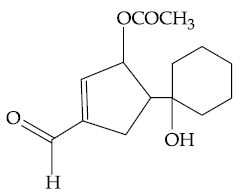
60. The major product formed in the following reaction is :

(1) 
(2) 
(3) 
(4) 
61. Let f : A → B be a function defined as ![]() where A = R – {2} and B R – {1}. Then f is :
where A = R – {2} and B R – {1}. Then f is :
(1) invertible and ![]()
(2) invertible and ![]()
(3) invertible and ![]()
(4) not invertible
62. If f (x) is a quadratic expression such that f (1)+f (2)=0, and −1 is a root of f (x)=0, then the other root of f (x)=0 is :
(1) −5/8
(2) −8/5
(3) 5/8
(4) 8/5
63. If |z – 3 + 2i| ≤ 4 then the difference between the greatest value and the least value of |z| is :
(1) 2√13
(2) 8
(3) 4 + √13
(4) √13
64. Suppose A is any 3×3 non-singular matrix and (A − 3I) (A − 5I) = O, where I = I3 and O = O3. If αA + βA−1 = 4I, then α + β is equal to :
(1) 8
(2) 7
(3) 13
(4) 12
65. If the system of linear equations
x + ay + z = 3
x + 2y + 2z = 6
x + 5y + 3z = b
has no solution, then :
(1) a=−1, b=9
(2) a=−1, b ≠ 9
(3) a ≠−1, b=9
(4) a=1, b ≠ 9
66. The number of four letter words that can be formed using the letters of the word BARRACK is :
(1) 120
(2) 144
(3) 264
(4) 270
67. The coefficient of x10 in the expansion of (1+x)2(1+x2)3(1+x3)4 is equal to :
(1) 52
(2) 56
(3) 50
(4) 44
68. If a, b, c are in A.P. and a2, b2, c2 are in G.P. such that a < b < c and ![]() then the value of a is :
then the value of a is :
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
69. Let  and Bn = 1 – An. Then, the least odd natural number p, so that Bn > An, for all n ≥ p, is :
and Bn = 1 – An. Then, the least odd natural number p, so that Bn > An, for all n ≥ p, is :
(1) 9
(2) 7
(3) 11
(4) 5
70. 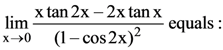
(1) 1/4
(2) 1
(3) 1/2
(4) −1/2
71. Let 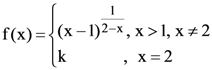
The value of k for which f is continuous at x = 2 is :
(1) 1
(2) e
(3) e−1
(4) e−2
72. If  equals :
equals :
(1) −√3 loge √3
(2) √3 loge √3
(3) −√3 loge 3
(4) √3 loge 3
73. Let f (x) be a polynomial of degree 4 having extreme values at x = 1 and x = 2.
If 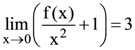 then f(−1) is equal to :
then f(−1) is equal to :
(1) 9/2
(2) 5/2
(3) 3/2
(4) 1/2
74. If 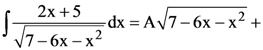

(where C is a constant of integration), then the ordered pair (A, B) is equal to :
(1) (2, 1)
(2) (−2, −1)
(3) (−2, 1)
(4) (2, −1)
75. The value of integral  is :
is :
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
76. If 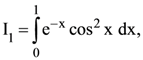
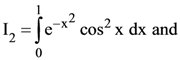
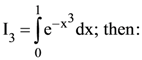
(1) I2 > I3 > I1
(2) I2 > I1 > I3
(3) I3 > I2 > I1
(4) I3 > I1 > I2
77. The curve satisfying the differential equation, (x2 − y2)dx+2xydy=0 and passing through the point (1, 1) is :
(1) a circle of radius one.
(2) a hyperbola.
(3) an ellipse.
(4) a circle of radius two.
78. The sides of a rhombus ABCD are parallel to the lines, x−y+2=0 and 7x−y+3=0. If the diagonals of the rhombus intersect at P(1, 2) and the vertex A (different from the origin) is on the y-axis, then the ordinate of A is :
(1) 5/2
(2) 7/4
(3) 2
(4) 7/2
79. The foot of the perpendicular drawn from the origin, on the line, 3x+y=λ(λ ≠ 0) is P. If the line meets x-axis at A and y-axis at B, then the ratio BP : PA is :
(1) 1 : 3
(2) 3 : 1
(3) 1 : 9
(4) 9 : 1
80. The tangent to the circle C1 : x2+y2 − 2x−1=0 at the point (2, 1) cuts off a chord of length 4 from a circle C2 whose centre is (3, −2). The radius of C2 is :
(1) 2
(2) √2
(3) 3
(4) √6
81. Tangents drawn from the point (−8, 0) to the parabola y2 = 8x touch the parabola at P and Q. If F is the focus of the parabola, then the area of the triangle PFQ (in sq. units) is equal to :
(1) 4x2 + 9y2 = 121
(2) 9x2 + 4y2 = 169
(3) 4x2 – 9y2 = 121
(4) 9x2 – 4y2 = 169
82. A normal to the hyperbola, 4x2 − 9y2 = 36 meets the co-ordinate axes x and y at A and B, respectively. If the parallelogram OABP (O being the origin) is formed, then the locus of P is :
(1) 4x2 + 9y2 = 121
(2) 9x2 + 4y2 = 169
(3) 4x2 – 9y2 = 121
(4) 9x2 – 4y2 = 169
83. An angle between the lines whose direction cosines are given by the equations, l + 3m + 5n = 0 and 5lm −2mn + 6nl = 0, is :
(1) cos−1 (1/3)
(2) cos−1 (1/4)
(3) cos−1 (1/6)
(4) cos−1 (1/8)
84. A plane bisects the line segment joining the points (1, 2, 3) and (−3, 4, 5) at right angles. Then this plane also passes through the point :
(1) (−3, 2, 1)
(2) (3, 2, 1)
(3) (−1, 2, 3)
(4) (1, 2, −3)
85. If the position vectors of the vertices A, B and C of a ∆ABC are respectively ![]() and
and ![]() then the position vector of the point, where the bisector of ∠A meets BC is :
then the position vector of the point, where the bisector of ∠A meets BC is :
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
86. A player X has a biased coin whose probability of showing heads is p and a player Y has a fair coin. They start playing a game with their own coins and play alternately. The player who throws a head first is a winner. If X starts the game, and the probability of winning the game by both the players is equal, then the value of ‘p’ is :
(1) 1/5
(2) 1/3
(3) 2/5
(4) 1/4
87. If the mean of the data : 7, 8, 9, 7, 8, 7, λ, 8 is 8, then the variance of this data is :
(1) 7/8
(2) 1
(3) 9/8
(4) 2
88. The number of solutions of sin 3x=cos 2x, in the interval (π/2, π) is :
(1) 1
(2) 2
(3) 3
(4) 4
89. A tower T1 of height 60 m is located exactly opposite to a tower T2 of height 80 m on a straight road. From the top of T1, if the angle of depression of the foot of T2 is twice the angle of elevation of the top of T2, then the width (in m) of the road between the feet of the towers T1 and T2 is :
(1) 10√2
(2) 10√3
(3) 20√3
(4) 20√2
90. Consider the following two statements :
Statement p :
The value of sin 120° can be derived by taking θ = 240° in the equation ![]()
Statement q :
The angles A, B, C and D of any quadrilateral ABCD satisfy the equation ![]()
Then the truth values of p and q are respectively :
(1) F, T
(2) T, F
(3) T, T
(4) F, F
JEE Main Online Computer Based Test (CBT) Examination Held on 15-04-2018 Morning Question Paper With Answer Key
JEE Main Online Computer Based Test (CBT) Examination Held on 15-04-2018
PHYSICS
1. In a common emitter configuration with suitable bias, it is given that RL is the load resistance and RBE is small signal dynamic resistance (input side). Then, voltage gain, current gain and power gain are given, respectively, by :
β is current gain, IB, IC and IE are respectively base, collector and emitter currents.
(1) 
(2) 
(3) 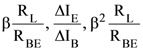
(4) 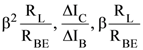
2. A thin uniform tube is bent into a circle of radius r in the vertical plane. Equal volumes of two immiscible liquids, whose densities are ρ1 and ρ2 (ρ1 > ρ2), fill half the circle. The angle θ between the radius vector passing through the common interface and the vertical is :
(1) 
(2) 
(3) 
(4) 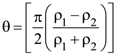
3. 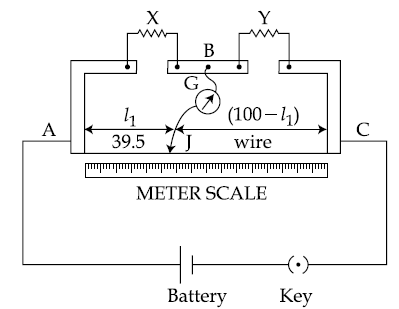
In a meter bridge, as shown in the figure, it is given that resistance Y = 12.5 Ω and that the balance is obtained at a distance 39.5 cm from end A (by Jockey J). After interchanging the resistances X and , a new balance point is found at a distance l2 from end A. What are the values of X and l2?
(1) 19.15 Ω and 39.5 cm
(2) 8.16 Ω and 60.5 cm
(3) 19.15 Ω and 60.5 cm
(4) 8.16 Ω and 39.5 cm
4. An automobile, travelling 40 km/h, can be stopped at a distance of 40 m by applying brakes. If the same automobile is travelling at 80 km/h, the minimum stopping distance, in metres, is (assume no skidding) :
(1) 160 m
(2) 75 m
(3) 150 m
(4) 100 m
5. A given object takes n times more time to slide down a 45° rough inclined plane as it takes to slide down a perfectly smooth 45° The coefficient of kinetic friction between the object and the incline is :
(1) ![]()
(2) 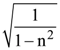
(3) 
(4) 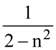
6. A body of mass M and charge q is connected to a spring of spring constant k. It is oscillating along x-direction about its equilibrium position, taken to be at x = 0, with an amplitude A. An electric field E is applied along the x-direction. Which of the following statements is correct?
(1) The new equilibrium position is at a distance ![]()
(2) The total energy of the system is ![]()
(3) The total energy of the system is ![]()
(4) The new equilibrium position is at a distance ![]()
7. The relative error in the determination of the surface area of a sphere is α. Then the relative error in the determination of its volume is :
(1) ![]()
(2) α
(3) ![]()
(4) ![]()
8. A monochromatic beam of light has a frequency ![]() and is propagating along the direction
and is propagating along the direction ![]() It is polarized along the
It is polarized along the![]() direction. The acceptable form for the magnetic field is :
direction. The acceptable form for the magnetic field is :
(1) 
(2) 
(3) 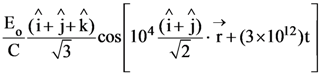
(4) 
9. The energy required to remove the electron from a singly ionized Helium atom is 2.2 times the energy required to remove an electron from Helium atom. The total energy required to ionize the Helium atom completely is :
(1) 109 eV
(2) 34 eV
(3) 79 eV
(4) 20 eV
10. An ideal capacitor of capacitance 0.2 μF is charged to a potential difference of 10 V. The charging battery is then disconnected. The capacitor is then connected to an ideal inductor of self inductance 0.5 mH. The current at a time when the potential difference across the capacitor is 5 V, is :
(1) 0.34 A
(2) 0.17 A
(3) 0.25 A
(4) 0.15 A
11. A Carnot’s engine works as a refrigerator between 250 K and 300 K. It receives 500 cal heat from the reservoir at the lower temperature. The amount of work done in each cycle to operate the refrigerator is :
(1) 420 J
(2) 2520 J
(3) 772 J
(4) 2100 J
12. A planoconvex lens becomes an optical system of 28 cm focal length when its plane surface is silvered and illuminated from left to right as shown in Fig-A.
If the same lens is instead silvered on the curved surface and illuminated from other side as in Fig. B, it acts like an optical system of focal length 10 cm. The refractive index of the material of lens is :
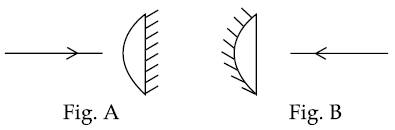
(1) 1.75
(2) 1.50
(3) 1.55
(4) 1.51
13. Two electrons are moving with non-relativistic speeds perpendicular to each other. If corresponding de Broglie wavelengths are λ1 and λ2, their de Broglie wavelength in the frame of reference attached to their centre of mass is :
(1) 
(2) 
(3) λCM = λ1 = λ2
(4) 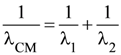
14. Take the mean distance of the moon and the sun from the earth to be 0.4 × 106 km and 150 × 106 km respectively. Their masses are 8 × 1022 kg and 2 × 1030 kg respectively. The radius of the earth is 6400 km. Let ∆F1 be the difference in the forces exerted by the moon at the nearest and farthest points on the earth and ∆F2 be the difference in the force exerted by the sun at the nearest and farthest points on the earth. Then, the number closest to ![]() is :
is :
(1) 10−2
(2) 2
(3) 0.6
(4) 6
15. The equivalent capacitance between A and B in the circuit given below, is :
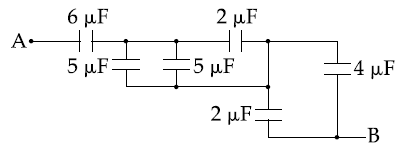
(1) 3.6 μF
(2) 4.9 μF
(3) 5.4 μF
(4) 2.4 μF
16. Light of wavelength 550 nm falls normally on a slit of width 22.0 × 10−5 The angular position of the second minima from the central maximum will be (in radians) :
(1) π/6
(2) π/4
(3) π/8
(4) π/12
17. A tuning fork vibrates with frequency 256 Hz and gives one beat per second with the third normal mode of vibration of an open pipe. What is the length of the pipe ? (Speed of sound in air is 340 ms−1)
(1) 190 cm
(2) 200 cm
(3) 220 cm
(4) 180 cm
18. A body of mass m is moving in a circular orbit of radius R about a planet of mass M. At some instant, it splits into two equal masses. The first mass moves in a circular orbit of radius R/2, and the other mass, in a circular orbit of radius 3R/2. The difference between the final and initial total energies is :
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
19. In a screw gauge, 5 complete rotations of the screw cause it to move a linear distance of 0.25 cm. There are 100 circular scale divisions. The thickness of a wire measured by this screw gauge gives a reading of 4 main scale divisions and 30 circular scale divisions. Assuming negligible zero error, the thickness of the wire is :
(1) 0.3150 cm
(2) 0.4300 cm
(3) 0.2150 cm
(4) 0.0430 cm
20. A solution containing active cobalt ![]() having activity of 0.8 μCi and decay constant λ is injected in an animal’s body. If 1 cm3 of blood is drawn from the animal’s body after 10 hrs of injection, the activity found was 300 decays per minute. What is the volume of blood that is flowing in the body? (1 Ci = 3.7 × 1010 decays per second and at t = 10 hrs e−λt = 0.84)
having activity of 0.8 μCi and decay constant λ is injected in an animal’s body. If 1 cm3 of blood is drawn from the animal’s body after 10 hrs of injection, the activity found was 300 decays per minute. What is the volume of blood that is flowing in the body? (1 Ci = 3.7 × 1010 decays per second and at t = 10 hrs e−λt = 0.84)
(1) 6 liters
(2) 5 liters
(3) 7 liters
(4) 4 liters
21. In the given circuit all resistances are of value R ohm each. The equivalent resistance between A and B is :
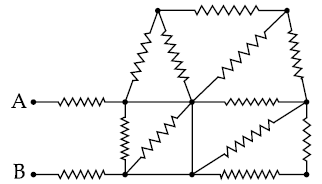
(1) 3R
(2) 2R
(3) 5R/3
(4) 5R/2
22. The velocity-time graphs of a car and a scooter are shown in the figure. (i) The difference between the distance travelled by the car and the scooter in 15 s and (ii) the time at which the car will catch up with the scooter are, respectively.

(1) 225.5 m and 10 s
(2) 112.5 m and 15 s
(3) 112.5 and 22.5 s
(4) 337.5 m and 25s
23. 
A uniform rod AB is suspended from a point X, at a variable distance x from A, as shown. To make the rod horizontal, a mass m is suspended from its end A. A set of (m, x) values is recorded. The appropriate variables that give a straight line, when plotted, are :
(1) m, 1/x
(2) m, x2
(3) m, x
(4) m, 1/x2
24. The number of amplitude modulated broadcast stations that can be accommodated in a 300 kHz band width for the highest modulating frequency 15 kHz will be :
(1) 8
(2) 15
(3) 10
(4) 20
25. A charge Q is placed at a distance a/2 above the centre of the square surface of edge as as shown in the figure

The electric flux through the square surface is :
(1) Q/ϵ0
(2) Q/6ϵ0
(3) Q/2ϵ0
(4) Q/3ϵ0
26. A Helmholtz coil has a pair of loops, each with N turns and radius R. They are placed coaxially at distance R and the same current I flows through the loops in the same direction. The magnitude of magnetic field at P, midway between the centres A and C, is given by [Refer to figure given below] :

(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
27. A particle is oscillating on the X-axis with an amplitude 2 cm about the point x0 = 10 cm, with a frequency ω. A concave mirror of focal length 5 cm is placed at the origin (see figure).
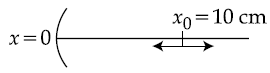
Identify the correct statements.
(A) The image executes periodic motion.
(B) The image executes non-periodic motion.
(C) The turning points of the image are asymmetric w.r.t. the image of the point at x = 10 cm.
(D) The distance between the turning points of the oscillation of the image is ![]()
(1) (B), (D)
(2) (B), (C)
(3) (A), (D)
(4) (A), (C), (D)
28. One mole of an ideal monoatomic gas is compressed isothermally in a rigid vessel to double pressure at room temperature, 27° The work done on the gas will be :
(1) 300 R ln 7
(2) 300 R ln 2
(3) 300 R
(4) 300 R ln 6
29. The B-H curve for a ferromagnet is sown in the figure. The ferromagnet is placed inside a long solenoid with 1000 turns/ cm. The current that should be passed in the solenoid to demagnetize the ferromagnet completely is :
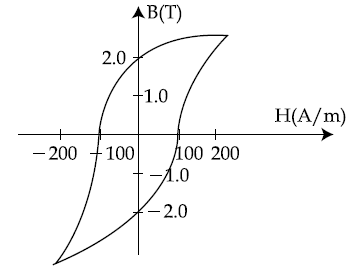
(1) 20 μA
(2) 40 μA
(3) 2 mA
(4) 1 mA
30. A force of 40 N acts on a point B at the end of an L-shaped object, as shown in the figure. The angle θ that will produce maximum moment of the force about point A is given by :
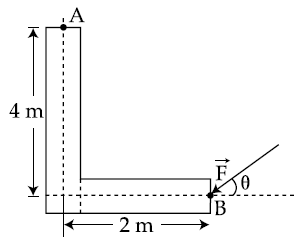
(1) tan θ = 2
(2) tan θ = 4
(3) tan θ = 1/2
(4) tan θ = 1/4
1. Which of the following statements about colloids is False?
(1) When excess of electrolyte is added to colloidal solution, colloidal particle will be precipitated.
(2) Colloidal particles can pass through ordinary filter paper.
(3) When silver nitrate solution is added to potassium iodide solution, a negatively charged colloidal solution is formed.
(4) Freezing pint of colloidal solution is lower than true solution at same concentration of a solute.
2. Ejection of the photoelectron from metal in the photoelectric effect experiment can be stopped by applying 0.5 V when the radiation of 250 nm is used. The work function of the metal is :
(1) 4.5 eV
(2) 5 eV
(3) 5.5 eV
(4) 4 eV
3. In which of the following reactions, an increase in the volume of the container will favour the formation of products?
(1) 2NO2(g) ⇌ 2NO(g) + O2(g)
(2) 4NH3(g) + 5O2(g) ⇌ 4NO(g) + 6H2O(l)
(3) 3O2(g) ⇌ 2O3(g)
(4) H2(g) + I2(g) ⇌ 2HI(g)
4. When an electric current is passed through acidified water, 112 mL of hydrogen gas at N.T.P. was collected at the cathode in 965 seconds. The current passed, in ampere, is :
(1) 0.5
(2) 0.1
(3) 1.0
(4) 2.0
5. ![]()

6. The decreasing order of bond angles in BF3, NH3, PF3 and I3− is :
(1) I3− > NH3 > PF3 > BF3
(2) BF3 > I3− > PF3 > NH3
(3) BF3 > NH3 > PF3 > I3−
(4) I3− > BF3 > NH3 > PF3
7. In graphite and diamond, the percentage of p-characters of the hybrid orbitals in hybridization are respectively :
(1) 33 and 25
(2) 33 and 75
(3) 67 and 75
(4) 50 and 75
8. A sample of NaClO3 is converted by heat to NaCl with a loss of 0.16 g of oxygen. The residue is dissolved in water and precipitated as AgCl. The mass of AgCl (in g) obtained will be : (Given : Molar mass of AgCl = 143.5 g mol−1)
(1) 0.54
(2) 0.41
(3) 0.48
(4) 0.35
9. N2O5 decomposes to NO2 and O2 and follows first order kinetics. After 50 minutes, the pressure inside the vessel increases from 50 mmHg to 8.75 mmHg. The pressure of the gaseous mixture after 100 minute at constant temperature will be :
(1) 116.25 mmHg
(2) 106.25 mmHg
(3) 136.25 mmHg
(4) 175.0 mmHg
10. Which of the following arrangements shows the schematic alignment of magnetic moments of antiferromagnetic substance?
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
11. The IUPAC name of the following compound is :

(1) 3-ethyl-4-methylhex-4-ene
(2) 4, 4-dithyl-3-methylbut-2-ene
(3) 4-methyl-3-ethylhex-4-ene
(4) 4-ethyl-3-methylhex-2-ene
12. For which of the following reactions, ∆H is equal to ∆U?
(1) 2HI(g) → H2(g) + I2(g)
(2) 2NO2(g) → N2O4 (g)
(3) N2(g) + 3H2(g) → 2NH3(g)
(4) 2SO2(g) + O2(g) → 2SO3(g)
13. For Na+, Mg2+, F− and O2− ; the correct order of increasing ionic radii is :
(1) Na+ < Mg2+ < F− < O2−
(2) Mg2+ < O2− < Na+ < F−
(3) Mg2+ < Na+ < F− < O2−
(4) O2− < F− < Na+ < Mg2+
14. The minimum volume of water required to dissolve 0.1 g lead (II) chloride to get a saturated solution (Ksp of PbCl2 = 3.2 × 10−8; atomic mass of Pb = 207 u) is :
(1) 17.98 L
(2) 0.18 L
(3) 1.798 L
(4) 0.36 L
15. An ideal gas undergoes a cyclic process a show in Figure.

∆UBC = −5 kJ mol−1, qAB = 2 kJ mol−1
WAB = −5 kJ mol−1, WCA = 3 kJ mol−1
Heat absorbed by the system during process CA is :
(1) −5 kJ mol−1
(2) +5 kJ mol−1
(3) −18 kJ mol−1
(4) 18 kJ mol−1
16. The main reduction product of the following compound with NaBH4 in methanol is :
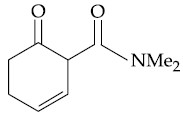
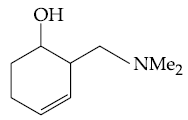
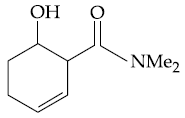
(1) 
(2) 
(3) 
(4) 
17. Which of the following will most readily give the dehydrohalogenation product?
(1) 
(2) 
(3) 
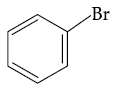
(4) 
18. The correct combination is :
(1) [NiCl4]2− −square-planar ; [Ni(CN)4] 2− −paramagnetic
(2) [NiCl4] 2− − diamagnetic; [Ni(CO)4] −square-planar
(3) [NiCl4] 2− − tetrahedral; [Ni(CO)4] –paramagnetic
(4) [NiCl4] 2− − paramagnetic; [Ni(CO)4] –tetrahedral
19. Which of the following is a Lewis acid?
(1) B(CH3)3
(2) PH3
(3) NF3
(4) NaH
20. The copolymer formed by addition polymerization of styrene and acrylonitrile in the presence of peroxide is
(1) 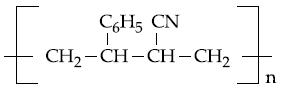
(2) 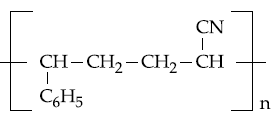
(3) 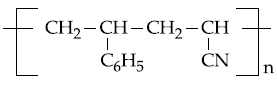
(4) 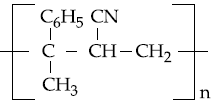
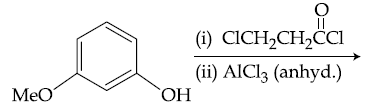
21. The major product of the following reaction is :
(1) 
(2) 
(3) 
(4) 
22. Xenon hexafluoride on partial hydrolysis produces compounds ‘X’ and ‘Y’ Compounds ‘X’ and ‘Y’ and the oxidation state of Xe are respectively :
(1) XeOF4 (+6) and XeO3 (+6)
(2) XeOF4 (+6) and XeO2F2 (+6)
(3) XeO2F2 (+6) and XeO2 (+4)
(4) XeO2 (+4) and XeO3 (+6)
23. The correct match between times of List-I and List-II is :

(1) (A)-(R), (B)-(P), (C)-(S), (D)-(Q)
(2) (A)-(R), (B)-(P), (C)-(Q), (D)-(S)
(3) (A)-(P), (B)-(S), (C)-(R), (D)-(Q)
(4) (A)-(R), (B)-(S), (C)-(P), (D)-(Q)
24. A white sodium salt dissolves readily in water to give a solution which is neutral to litmus. When silver nitrate solution is added to the aforementioned solution, a white precipitate is obtained which does not dissolve in dil. nitric acid. The anion is :
(1) SO42−
(2) CO32−
(3) Cl−
(4) S2−
25. In the molecular orbital diagram for the molecular ion, N2+, the number of electrons in the σ2p molecular orbital is :
(1) 2
(2) 1
(3) 0
(4) 3
26. The reagent (s) required for the following conversion are :

(1) (i) B2H6 (ii) SnCl2/HCl (iii) H3O+
(2) (i) B2H6 (ii) DIBAL-H (iii) H3O+
(3) (i) LiAlH4 (ii) H3O+
(4) (i) NaBH4 (ii) Raney Ni/H2 (iii) H3O+
27. Which of the following is the correct structure of Adenosine?
(1) 
(2) 
(3) 
(4) 
28. Identify the pair in which the geometry of the species is T-shape and square-pyramidal, respectively :
(1) IO3− and IO2F2−
(2) XeOF2 and XeOF4
(3) ICl2− and ICl5
(4) ClF3 and IO4−
29. Which of the following will not exist in zwitter ionic from at pH = 7?
(1) 
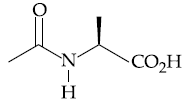
(2) 
(3) 
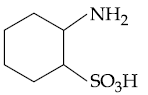
(4) 
30. The increasing order of nitration of the following compounds is :

(1) (a) < (b) < (d) < (c)
(2) (b) < (a) < (d) < (c)
(3) (b) < (a) < (c) < (d)
(4) (a) < (b) < (c) < (d)
1. Consider the following two binary relations on the set A = {a, b, c} :
R1 = {(c, a), (b, b), (a, c), (c, c), (b, c), (a, a)} and
R2 = {(a, b), (b, a), (c, c), (c, a), (a, a), (b, b), (a, c)}.
Then :
(1) R1 is not symmetric but it is transitive.
(2) both R1 and R2 are transitive.
(3) both R1 and R2 are not symmetric.
(4) R2 is symmetric but it is not transitive.
2. A box ‘A’ contains 2 white, 3 red and 2 black balls. Another box ‘B’ contains 4 white, 2 red and 3 black balls. If two balls are drawn at random, without replacement, from a randomly selected box and one ball turns out to be white while the other ball turns out to be red, then the probability that both balls are drawn from box ‘B’ is :
(1) 7/16
(2) 7/8
(3) 9/32
(4) 9/16
3. An angle between the plane, x + y + z = 5 and the line of intersection of the planes, 3x + 4y + z – 1 = 0 and 5x + 8y + 2z + 14 = 0, is :
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
4. Two parabolas with a common vertex and with axes long x-axis and y-axis, respectively, intersect each other in the first quadrant. If the length of the latus rectum of each parabola is 3, then the equation of the common tangent to the two parabolas is :
(1) x + 2y + 3 = 0
(2) 4(x + y) + 3 = 0
(3) 3(x + y) + 4 = 0
(4) 8(2x + y) + 3 = 0
5. If x1, x2, . . ., xn and  are two A.P.s such that x3 = h2 = 8 and x8 = h7 = 20, then x5∙h10 equals :
are two A.P.s such that x3 = h2 = 8 and x8 = h7 = 20, then x5∙h10 equals :
(1) 3200
(2) 2560
(3) 2650
(4) 1600
6. If (P ⋀ ~q) ⋀ (p ⋀ r) → ~ p ⋁ q is false, then the truth values of p, q and r are, respectively :
(1) T, F, T
(2) F, F, F
(3) F, T, F
(4) T, T, T
7. Let S be the set of all real values of k for which the system of linear equations
x + y + z = 2
2x + y – z = 3
3x + 2y + kz = 4
has a unique solution. Then S is :
(1) an empty set
(2) equal to R – {0}
(3) equal to R
(4) equal to {0}
8. The area (i9n sq. units) of the region {x ϵ R : x ≥ 0, y ≥ 0, y ≥ x – 2 and y ≤ √x}, is :
(1) 13/3
(2) 10/3
(3) 5/3
(4) 8/3
9. If the tangents drawn to the hyperbola 4y2 = x2 + 1 intersect the co-ordinate axes at the distinct points A and B, then the locus of the mid point of AB is :
(1) x2 – 4y2 + 16x2y2 = 0
(2) 4x2 – y2 – 16x2y2 = 0
(3) 4x2 – y2 + 16x2y2 = 0
(4) x2 – 4y2 – 16x2y2 = 0
10. If β is one of the angles between the normals to the ellipse, x2 + 3y2 = 9 at the points (3 cos θ, √3 sinθ) and (−3 sin θ, √3 cos θ); 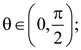 then
then ![]() is equal to :
is equal to :
(1) √3/4
(2) 2/√3
(3) √2
(4) 1/√3
11. If ![]() are unit vectors such that
are unit vectors such that ![]() is equal to :
is equal to :
(1) √15/4
(2) √15/16
(3) 15/16
(4) 1/4
12. n-digit numbers are formed suing only three digits 2, 5 and 7. The smallest value of n for which 900 such distinct numbers can be formed, is :
(1) 9
(2) 6
(3) 7
(4) 8
13. If x2 + y2 + sin y = 4, then the value of ![]() at the point (−2, 0) is :
at the point (−2, 0) is :
(1) −34
(2) −32
(3) 4
(4) −2
14. If tan A and tan B are the roots of the quadratic equation, 3x2 – 10x – 25 = 0, then the value of 3 sin2(A + B) – 10 sin(A + B) ∙ cos(A + B) – 25 cos2(A + B) is :
(1) 25
(2) 10
(3) −25
(4) −10
15. The value of the integral 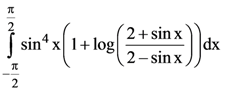 is :
is :
(1) ![]()
(2) 3/4
(3) ![]()
(4) 0
16. The set of all α ϵ R, for which ![]() is a purely imaginary number, for all z ϵ C satisfying |z| = 1 and Re z ≠ 1 is :
is a purely imaginary number, for all z ϵ C satisfying |z| = 1 and Re z ≠ 1 is :
(1) equal to R
(2) an empty set
(3) {0}
(4) ![]()
17. Let y = (x) be the solution of the differential equation ![]() where
where

If y (0) = 0, the ![]() is :
is :
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
18. A variable plane passes through a fixed point (3, 2, 1) and meets x, y and z axes at A, B and C respectively. A plane is drawn parallel to yz-plane through A, a second plane is drawn parallel zx-plane through B and a third plane is drawn parallel to xy-plane through C. Then the locus of the point of intersection of these three planes, is :
(1) ![]()
(2) ![]()
(3) ![]()
(4) x + y + z = 6
19. The mean of a set of 30 observations is 75. If each observation is multiplied by a non-zero number λ and then each of them is decreased by 25, their mean remains the same. Then λ is equal to :
(1) 4/3
(2) 1/3
(3) 2/3
(4) 10/3
20. Let S = {λ, μ) ϵ R × R : f(t) = (|λ| e|t| − μ), sin (2|t|), t ϵ R, is a differentiable function}. Then S is a subset of :
(1) R × (−∞, 0)
(2) R × [0, ∞)
(3) [0, ∞) × R
(4) (−∞, 0) × R
21. If n is the degree of the polynomial, 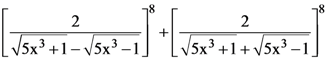 and m is the coefficient of xn in it, then the ordered pair (n, m) is equal to :
and m is the coefficient of xn in it, then the ordered pair (n, m) is equal to :
(1) (12, (20)4)
(2) (8, 5(10)4)
(3) (24, (10)8)
(4) (12, 8(10)4)
22. An aeroplane flying at a constant speed, parallel to the horizontal ground, √3 km above it, is observed at an elevation of 60° from a point on the ground. If, after five seconds, its elevation from the same point, is 30°, then the speed (in km/hr) of the aeroplane, is :
(1) 750
(2) 1440
(3) 1500
(4) 720
23. If b is the first term of an infinite G.P. whose sum is five, then b lies in the interval :
(1) [10, ∞)
(2) (−∞, −10]
(3) (−10, 0)
(4) (0, 10)
24. Let A be a matrix such that  is a scalar matrix and |3A| = 108. Then A2 equals :
is a scalar matrix and |3A| = 108. Then A2 equals :
(1) 
(2) 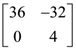
(3) 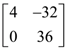
(4) 
25. If a right circular cone, having maximum volume, is inscribed in a sphere of radius 3 cm, then the the curved surface area (in cm2) of this cone is :
(1) 8√3 π
(2) 8√2 π
(3) 6√2 π
(4) 6√3 π
26. If 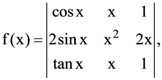 then
then ![]()
(1) does not exist.
(2) exists and is equal to 0.
(3) exists and is equal to 2.
(4) exists and is equal to −2.
27. If λ ϵ R is such that the sum of the cubes of the roots of the equation, x2 + (2 – λ)x + (10 – λ) = 0 is minimum, then the magnitude of the difference of the roots of this equation is :
(1) 4√2
(2) 20
(3) 20√5
(4) 2√7
28. A circle passes through the points (2, 3) and (4, 5). If its centre lies on the line, y – 4x + 3 = 0, then its radius is equal to :
(1) 2
(2) √2
(3) √5
(4) 1
29. In a triangle ABC, coordinates of A are (1, 2) and the equations of the medians through B and C are respectively, x + y = 5 and x = 4. Then area of ∆ABC (in sq. units) is :
(1) 12
(2) 4
(3) 5
(4) 9
30. If ![]() then ∫f(x) dx is equal to :
then ∫f(x) dx is equal to :
(where C is a constant of integration)
(1) 12 loge |1 – x| − 3x + C
(2) −12 loge |1 – x| + 3x + C
(3) −12 loge |1 – x| − 3x + C
(4) 12 loge |1 – x| + 3x + C
JEE Main Offline Examination Held on 08-04-2018 Code A Question Paper With Answer Key
JEE Main Offline Examination Held on 08-04-2018 Code A
1. The density of a material in the shape of a cube is determined by measuring three sides of the cube and its mass. If the relative errors in measuring the mass and length are respectively 1.5% and 1%, the maximum error in determining the density is
(1) 2.5%
(2) 3.5%
(3) 4.5%
(4) 6%
2. All the graphs below are intended to represent the same motion. One of them does it incorrectly. Pick it up.
(1) 
(2) 
(3) 
(4) 
3. Two masses m1= 5 kg and m2= 10 kg, connected by an inextensible string over a frictionless pulley, are moving as shown in the figure. The coefficient of friction of horizontal surface is 0.15. The minimum weight m that should be put on top of m2 to stop the motion is
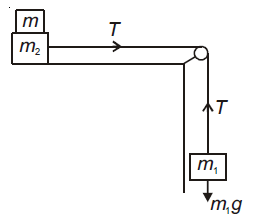
(1) 18.3 kg
(2) 27.3 kg
(3) 43.3 kg
(4) 10.3 kg
4. A particle is moving in a circular path of radius a under the action of an attractive potential ![]() Its total energy is
Its total energy is
(1) ![]()
(2) ![]()
(3) Zero
(4) ![]()
5. In a collinear collision, a particle with an initial speed v0 strikes a stationary particle of the same mass. If the final total kinetic energy is 50% greater than the original kinetic energy, the magnitude of the relative velocity between the two particles, after collision, is
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
6. Seven identical circular planar disks, each of mass M and radius R are welded symmetrically as shown. The moment of inertia of the arrangement about the axis normal to the plane and passing through the point P is

(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
7. From a uniform circular disc of radius R and mass 9M, a small disc of radius R/3 is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is
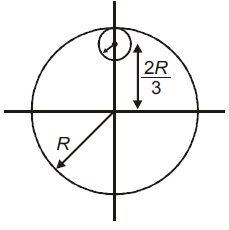
(1) 4MR2
(2) ![]()
(3) 10MR2
(4) ![]()
8. A particle is moving with a uniform speed in a circular orbit of radius R in a central force inversely proportional to the nth power of R. If the period of rotation of the particle is T, then
(1) T ∝ R3/2 for any n
(2) ![]()
(3) T ∝ R(n + 1)/2
(4) T ∝ Rn/2
9. A solid sphere of radius r made of a soft material of bulk modulus K is surrounded by a liquid in a cylindrical container. A massless piston of area of a floats on the surface of the liquid, covering entire cross-section of cylindrical container. When a mass m is placed on the surface of the piston to compress the liquid, the fractional decrement in the radius of the sphere, (dr/r), is
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
10. Two moles of an ideal monoatomic gas occupies a volume V at 27°C. The gas expands adiabatically to a volume 2 V. Calculate (a) the final temperature of the gas and (b) change in its internal energy.
(1) (a) 189 K (b) 2.7 kJ
(2) (a) 1195 K (b) −2.7 kJ
(3) (a) 189 K (b) −2.7 kJ
(4) (a) 195 K (b) 2.7 kJ
11. The mass of a hydrogen molecule is 3.32 × 10−27 If 1023 hydrogen molecules strike, per second, a fixed wall of area 2 cm2 at an angle of 45° to the normal, and rebound elastically with a speed of 103 m/s, then the pressure on the wall is nearly
(1) 2.34 × 103 N/m2
(2) 4.70 × 103 N/m2
(3) 2.35 × 102 N/m2
(4) 4.70 × 102 N/m2
12. A silver atom in a solid oscillates in simple harmonic motion in some direction with a frequency of 1012/second. What is the force constant of the bonds connecting one atom with the other? (Mole wt. of silver = 108 and Avagadro number = 6.02 × 1023 gm mole−1)
(1) 6.4 N/m
(2) 7.1 N/m
(3) 2.2 N/m
(4) 5.5 N/m
13. A granite rod of 60 cm length is clamped at its middle point and is set into longitudinal vibrations. The density of granite is 2.7 × 103 kg/m3 and its Young’s modulus is 9.27 × 1010 What will be the fundamental frequency of the longitudinal vibrations?
(1) 5 kHz
(2) 2.5 kHz
(3) 10 kHz
(4) 7.5 kHz
14. Three concentric metal shells A, B and C of respective radii a, b and c (a < b < c) have surface charge densities +σ, −σ and + σ respectively. The potential of shell B is
(1) 
(2) 
(3) 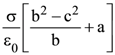
(4) 
15. A parallel plate capacitor of capacitance 90 pF is connected to a battery of emf 20 V. If a dielectric material of dielectric constant K = 5/3 is inserted between the plates, the magnitude of the induced charge will be
(1) 1.2 nC
(2) 0.3 nC
(3) 2.4 nC
(4) 0.9 nC
16. In an a.c. circuit, the instantaneous e.m.f. and current are given by
e = 100 sin 30t
![]()
In one cycle of a.c., the average power consumed by the circuit and the wattless current are, respectively
(1) 50, 10
(2) ![]()
(3) ![]()
(4) 50, 0
17. Two batteries with e.m.f 12 V and 13 V are connected in parallel across a load resistor of 10 Ω. The internal resistances of the two batteries are 1 Ω and 2 Ω respectively. The voltage across the load lies between
(1) 11.6 V and 11.7 V
(2) 11.5 V and 11.6 V
(3) 11.4 V and 11.5 V
(4) 11.7 V and 11.8 V
18. An electron, a proton and an alpha particle having the same kinetic energy are moving in circular orbits of radii re, rp, rα respectively in a uniform magnetic field B. The relation between re, rp, rα is
(1) re > rp = rα
(2) re < rp = rα
(3) re < rp < rα
(4) re < rα < rp
19. The dipole moment of a circular loop carrying a current I, is m and the magnetic field at the centre of the loop is B1. When the dipole moment is doubled by keeping the current constant, the magnetic field at the centre of the loop is B2. The ratio B1/B2 is
(1) 2
(2) ![]()
(3) ![]()
(4) ![]()
20. For an RLC circuit driven with voltage of amplitude vm and frequency ![]() the current exhibits resonance. The quality factor, Q is given by
the current exhibits resonance. The quality factor, Q is given by
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
21. An EM wave from air enters a medium. The electric fields are 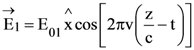 in air and
in air and ![]() in medium, where the wave number k and frequency ν refer to their values in air. The medium is non-magnetic. If
in medium, where the wave number k and frequency ν refer to their values in air. The medium is non-magnetic. If ![]() refer to relative permittivities of air and medium respectively, which of the following options is correct?
refer to relative permittivities of air and medium respectively, which of the following options is correct?
(1) 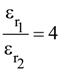
(2) 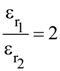
(3) 
(4) 
22. Unpolarized light of intensity I passes through an ideal polarizer A. Another identical polarizer B is placed behind A. The intensity of light beyond B is found to be I/2. Now another identical polarizer C is placed between A and B. The intensity beyond B is now found to be I/8. The angle between polarizer A and C is
(1) 0°
(2) 30°
(3) 45°
(4) 60°
23. The angular width of the central maximum in a single slit diffraction pattern is 60°. The width of the slit is 1 μm. The slit is illuminated by monochromatic plane waves. If another slit of same width is made near it, Young’s fringes can be observed on a screen placed at a distance 50 cm from the slits. If the observed fringe width is 1 cm, what is slit separation distance?
(i.e. distance between the centres of each slit.)
(1) 25 μm
(2) 50 μm
(3) 75 μm
(4) 100 μm
24. An electron from various excited states of hydrogen atom emit radiation to come to the ground state. Let λn, λg be the de Broglie wavelength of the electron in then nth state and the ground state respectively. Let Λn be the wavelength of the emitted photo in the transition from the nth state to the ground state. For large n, (A, B are constants)
(1) 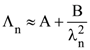
(2) Λn ≈ A + Bλn
(3) ![]()
(4) ![]()
25. If the series limit frequency of the Lyman series is νL, then the series limit frequency of the P fund series is
(1) 25 νL
(2) 16 νL
(3) νL/16
(4) νL/25
26. It is found that if a neutron suffers an elastic collinear collision with deuterium at rest, fractional loss of its energy is pd; while for its similar collision with carbon nucleus at rest, fractional loss of energy is pd and pc are respectively
(1) (.89, .28)
(2) (.28, .89)
(3) (0, 0)
(4) (0, 1)
27. The reading of the ammeter for a silicon diode in the given circuit is

(1) 0
(2) 15 mA
(3) 11.5 mA
(4) 13.5 mA
28. A telephonic communication service is working at carrier frequency of 10 GHz. Only 10% of it is utilized for transmission. How many telephonic channels can be transmitted simultaneously if each channel requires a bandwidth of 5 kHz?
(1) 2 × 103
(2) 2 × 104
(3) 2 × 105
(4) 2 × 106
29. In a potentiometer experiment, it is found that no current passes through the galvanometer when the terminals of the cell are connected across 52 cm of the potentiometer wire. If the cell is shunted by a resistance of 5 Ω, a balance is found when the cell is connected across 40 cm of the wire. Find the internal resistance of the cell.
(1) 1 Ω
(2) 1.5 Ω
(3) 2 Ω
(4) 2.5 Ω
30. On interchanging the resistances, the balance point of a meter bridge shifts to the left by 10 cm. The resistance of their series combination is 1 kΩ. How much was the resistance on the left slot before interchanging the resistances?
(1) 990 Ω
(2) 505 Ω
(3) 550 Ω
(4) 910 Ω
31. The ratio of mass percent of C and H of an organic compound (CXHYOZ) is 6 : 1. If one molecule of the above compound (CXHYOZ) contains half as much oxygen as required to burn one molecule of compound CXHY completely CO2 and H2 The empirical formula of compound CXHYOZ is
(1) C3H6O3
(2) C2H4O
(3) C3H4O2
(4) C2H4O3
32. Which type of ‘defect’ has the presence of cations in the interstitial sites?
(1) Schottky defect
(2) Vacancy defect
(3) Frenkel defect
(4) Metal deficiency defect
33. According to molecular orbital theory, which of the following will not be a viable molecule?
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
34. Which of the following lines correctly show the temperature dependence of equilibrium constant K, for an exothermic reaction?

(1) A and B
(2) B and C
(3) C and D
(4) A and D
35. The combustion of benzene (l) gives CO2 (g) and H2O(I). Given that heat of combustion of benzene at constant volume is –3263.9 kJ mol−1 at 25°C; heat of combustion (in kJ mol−1) of benzene at constant pressure will be
(R = 8.314 JK−1 mol−1)
(1) 4152.6
(2) −452.46
(3) 3260
(4) −3267.6
36. For 1 molal aqueous solution of the following compounds, which one will show the highest freezing point?
(1) [Co(H2O)6]Cl3
(2) [Co(H2O)5Cl]Cl2 ∙ H2O
(3) [Co(H2O)4Cl2]Cl ∙ 2H2O
(4) [Co(H2O)3Cl3] ∙ 3H2O
37. An aqueous solution contains 0.10 M H2S and 0.20 M HCl. If the equilibrium constant for the formation of HS− from H2S is 1.0 × 10−7 and that of S2− from HS− ions is 1.2 × 10−13 then the concentration of S2− ions in aqueous solution is
(1) 5 × 10−8
(2) 3 × 10−20
(3) 6 × 10−21
(4) 5 × 10−19
38. An aqueous solution contains an unknown concentration of Ba2+. When 50 mL of a 1 M solution of Na2SO4 is added, BaSO4 just begins to precipitate. The final volume is 500 mL. The solubility product of BaSO4 is 1 × 10−10. What is original concentration of Ba2+?
(1) 5 × 10−9 M
(2) 2 × 10−9 M
(3) 1.1 × 10−9 M
(4) 1.0 × 10−10 M
39. At 518°C, the rate of decomposition of a sample of gaseous acetaldehyde, initially at a pressure of 363 torr, was 1.00 torr s−1 when 5% had reacted and 0.5 torr s−1 when 33% had reacted. The order of the reaction is
(1) 2
(2) 3
(3) 1
(4) 0
40. How long (approximate) should water be electrolysed by passing through 100 amperes current so that the oxygen released can completely burn 27.66 g of diborane? (Atomic weight of B = 10.8 u)
(1) 6.4 hours
(2) 0.8 hours
(3) 3.2 hours
(4) 1.6 hours
41. The recommended concentration of fluoride ion in drinking water is up to 1 ppm as fluoride ion is required to make teeth enamel harder by converting [3Ca3(PO4)2 . Ca(OH)2] to
(1) [CaF2]
(2) [3(CaF2). Ca(OH)2]
(3) [3Ca3(PO4)2. CaF2]
(4) [3{Ca(OH)2}. CaF2]
42. Which of the following compounds contain(s) no covalent bond(s)?
KCl, PH3, O2, B2H6, H2SO4
(1) KCl, B2H6, PH3
(2) KCl2, H2SO4
(3) KCl
(4) KCl, B2H2
43. Which of the following are Lewis acids?
(1) PH3 and BCl3
(2) AlCl3 and SiCl4
(3) PH3 and SiCl4
(4) BCl3 and AlCl3
44. Total number of lone pair of electron in ![]() ion is
ion is
(1) 3
(2) 6
(3) 9
(4) 12
45. Which of the following salts is the most basic in aqueous solution?
(1) Al(CN)3
(2) CH3COOK
(3) FeCl3
(4) Pb(CH3COO)2
46. Hydrogen peroxide oxidises [Fe(CN)6]4− to [Fe(CN)6] 3− in acidic medium but reduces [Fe(CN)6] 3− to [Fe(CN)6] 4− in alkaline medium. The other product formed are, respectively.
(1) (H2O + O2) and H2O
(2) (H2O + O2) and (H2O + OH–)
(3) H2O and (H2O + O2)
(4) H2O and (H2O + OH–)
47. The oxidation states of
Cr in [Cr(H2O)6]Cl3, [Cr(C6H6)2], and K2[Cr(CN)2(O)2 (NH3)] respectively are
(1) +3 , +4 and +6
(2) +3, +2, and +4
(3) +3, 0and +6
(4) +3, 0 and +4
48. The compound that does not produce nitrogen gas by the thermal decomposition is
(1) Ba(N3)2
(2) (NH4)2Cr2O7
(3) NH4NO2
(4) (NH4)2SO4
49. When metal ‘M’ is treated with NaOH, a white gelatinous precipitate ‘X’ is obtained, which is soluble in excess of NaOH. Compound ‘X’ when heated strongly gives an oxide which is used in chromatography as an adsorbent. The metal ‘M’ is
(1) Zn
(2) Ca
(3) Al
(4) Fe
50. Consider the following reaction and statements
[Co(NH3)4Br2]+ + Br− → [Co(NH3)3Br3] + NH3
(I) Two isomers are produced if the reactant complex ion is a cis-isomer
(II) Two isomers are produced if the reactant complex ion is a trans-isomer.
(III) Only one isomer is produced if the reactant complex ion is a trans-isomer.
(IV) Only one isomer is produced if the reactant complex ion is a cis-isomer.
The correct statements are:
(1) (I) and (II)
(2) (I) and (III)
(3) (III) and (IV)
(4) (II) and (IV)
51. Glucose on prolonged heating with HI gives
(1) n-Hexane
(2) 1-Hexene
(3) Hexanoic acid
(4) 6-iodohexanal
52. The trans-alkenes are formed by the reduction of alkynes with
(1) H2 – Pd/C, BaSO4
(2) NaBH4
(3) Na/liq. NH3
(4) Sn – HCl
53. Which of the following compounds will be suitable for Kjeldahl’s method for nitrogen estimation?
(1) 
(2) 
(3) 
(4) 
54. Phenol on treatment with CO2 in the presence of NaOH followed by acidification produces compound X as the major product. X on treatment with (CH3CO)2O in the presence of catalytic amount of H2SO4 produces
(1) 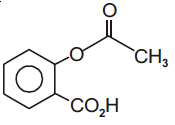
(2) 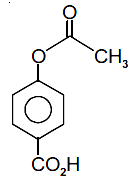
(3) 
(4) 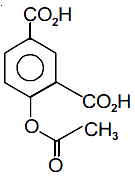
55. An alkali is titrated against an acid with methyl orange as indicator, which of the following is a correct combination?

56. The predominant form of histamine present in human blood is (pKa, Histidine = 6.0)
(1) 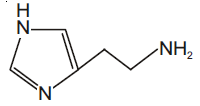
(2) 
(3) 
(4) 
57. Phenol reacts with methyl chloroformate in the presence of NaOH to form product A. A reacts with Br2 to form product B. A and B are respectively
(1) 
(2) 
(3) 
(4) 
58. The increasing order of basicity of the following compound is

(1) (a) < (b) < (c) < (d)
(2) (b) < (a) < (c) < (d)
(3) (b) < (a) < (d) < (c)
(4) (d) < (b) < (a) < (c)
59. The major product formed in the following reaction is
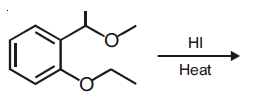
(1) 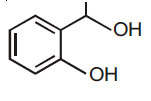
(2) 
(3) 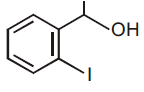
(4) 
60. The major product of the following reaction is
(1) 
(2) 
(3) 
(4) 
61. Two sets A and B are as under :
A = {(a, b) ∈ R × R : |a – 5| < 1 and |b – 5| < 1}
B = {(a, b) ∈ R × R : 4(a – 6)2 + 9(b – 5)2 ≤ 36},
then
(1) B ⊂ A
(2) A ⊂ B
(3) A ∩ B = ϕ (an empty set)
(4) Neither A ⊂ B nor B ⊂ A
62. Let S = {x ∈ R : x ≥ 0 and 2|√x – 3| + √x(√x – 6) + 6 = 0}. Then S :
(1) Is an empty set
(2) Contains exactly one element
(3) Contains exactly two elements
(4) Contains exactly four elements
63. If α, β ∈ C are the distinct roots, of the equation x2 – x + 1= 0, then α101 + β107 is equal to
(1) −1
(2) 0
(3) 1
(4) 2
64. If  then the ordered pair (A, B) is equal to
then the ordered pair (A, B) is equal to
(1) (−4, −5)
(2) (−4, 3)
(3) (−4, 5)
(4) (4, 5)
65. If the system of linear equations
x + ky + 3z = 0
3x + ky – 2z = 0
2x + 4y – 3z = 0
has a non-zero solution (x, y, z), then xz/y2 is equal to
(1) –10
(2) 10
(3) –30
(4) 30
66. From 6 different novels and 3 different dictionaries, 4 novels and 1 dictionary are to be selected and arranged in a row on a shelf so that the dictionary is always in the middle. The number of such arrangements is
(1) At least 1000
(2) Less then 500
(3) At least 500 but less than 750
(4) At least 750 but less than 1000
67. The sum of the co-efficients of all odd degree terms in the expansion of ![]() is
is
(1) −1
(2) 0
(3) 1
(4) 2
68. Let a1, a2, a3, …….., a49 be in A.P. such that
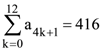 and a9 + a43 = 66.
and a9 + a43 = 66.
If ![]() then m is equal to
then m is equal to
(1) 66
(2) 68
(3) 34
(4) 33
69. Let A be the sum of the first 20 terms and B be the sum of the first 40 terms of the series 12 + 2.22 + 32 + 2.42 + 52 + 2.62 + ….
If B – 2A = 100λ, then λ is equal to
(1) 232
(2) 248
(3) 464
(4) 496
70. For each t ∈ R, let [t] be the greatest integers less than or equal to t. Then
![]()
(1) Is equal to 0
(2) Is equal to 15
(3) Is equal to 120
(4) Does not exist (in R)
71. Let S = {t ∈ R : f(x) = |x – π| ∙(|x| – 1)sin |x| is not differential at t}. Then the set S is equal to
(1) ϕ (an empty set)
(2) {0}
(3) {π}
(4) {0, π}
72. If the curves y2 = 6x, 9x2 + by2 = 16 intersect each other at right angles, then the value of b is
(1) 6
(2) 7/2
(3) 4
(4) 9/2
73. Let ![]() x ∈ R – {−1, 0, 1}. If
x ∈ R – {−1, 0, 1}. If ![]() then the local minimum value of h(X) is:
then the local minimum value of h(X) is:
(1) 3
(2) −3
(3) −2√2
(4) 2√2
74. The integral 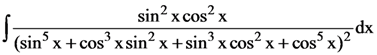 is equal to
is equal to
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
75. Then value of  is :
is :
(1) π/8
(2) π/2
(3) 4π
(4) π/4
76. Let g(x) = cos x2, f(x) = √x, and α, β (α < β) be the roots of the quadratic equation 18x2 – 9πx + π2 = 0. Then the area (in sq. units) bounded by the curve y = (gof) (x) and the lines x = α, x = β and y = 0 is
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
77. Let y = y(x) be the solution of the differential equation ![]() x ∈ (0, π. If
x ∈ (0, π. If ![]() then y(π/6) is equal to :
then y(π/6) is equal to :
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
78. A straight line through a fixed point (2, 3) intersects the coordinate axes at distinct points P and Q. If O is the origin and the rectangle OPRQ is completed, then the locus of R is
(1) 3x + 2y = 6
(2) 2x + 3y = xy
(3) 3x + 2y = xy
(4) 3x + 2y = 6xy
79. Let the orthocentre and centroid of a triangle be A(–3, 5) and B(3, 3) respectively. If C is the circumcentre of this triangle, then the radius of the circle having line segment AC as diameter, is
(1) √10
(2) 2√10
(3) ![]()
(4) ![]()
80. If the tangent at (1, 7) to the curve x2 = y – 6 touches the circle x2 + y2 + 16x + 12y + c = 0 then the value of c is
(1) 195
(2) 185
(3) 85
(4) 95
81. Tangent and normal are drawn at P(16, 16) on the parabola y2 = 16x, which intersect the axis of the parabola at A and B, respectively. If C is the centre of the circle through the points P, A and B and ∠CPB = θ, then a value of tan θ is
(1) 1/2
(2) 2
(3) 3
(4) 4/3
82. Tangents are drawn to the hyperbola 4x2 – y2 = 36 at the points P and Q. If these tangents intersect at the point T(0, 3) then the area (in sq. units) of ∆PTQ is
(1) 45√5
(2) 54√3
(3) 60√3
(4) 36√5
83. If L1 is the the line of intersection of the planes 2x – 2y + 3z – 2 = 0, x – y + z + 1 = 0 and L2 is the line of intersection of the planes x + 2y – z – 3 = 0, 3x – y + 2z – 1 = 0, then the distance of the origin from the plane containing the lines L1 and L2, is
(1) ![]()
(2) ![]()
(3) ![]()
(4) ![]()
84. The length of the projection of the line segment joining the points (5, –1, 4) and (4, –1, 3) on the plane, x + y + z = 7 is:
(1) 2/√3
(2) 2/3
(3) 1/3
(4) ![]()
85. Let ![]() be a vector coplanar with the vectors
be a vector coplanar with the vectors ![]() If
If ![]() is perpendicular to
is perpendicular to ![]() is equal to
is equal to
(1) 336
(2) 315
(3) 256
(4) 84
86. A bag contains 4 red and 6 black balls. A ball is drawn at random from the bag, its colour is observed and this ball along with two additional balls of the same colour are returned to the bag. If now a ball is drawn at random from the bag, then the probability that this drawn ball is red, is:
(1) 3/10
(2) 2/5
(3) 1/5
(4) 3/4
87. If  then the standard deviation of the 9 items x1, x2, …. ., x9 is
then the standard deviation of the 9 items x1, x2, …. ., x9 is
(1) 9
(2) 4
(3) 2
(4) 3
88. If sum of all the solutions of the equation 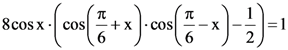 in [0, π] is kπ, then k is equal to :
in [0, π] is kπ, then k is equal to :
(1) 2/3
(2) 13/9
(3) 8/9
(4) 20/9
89. PQR is a triangular park with PQ = PR = 200 m. A T.V. tower stands at the mid-point of QR. If the angles of elevation of the top of the tower at P, Q and R are respectively 45º, 30º and 30º, then the height of the tower (in m) is
(1) 100
(2) 50
(3) 100√3
(4) 50√2
90. The Boolean expression ~ (p ⋁ q) ⋁ (~ p ⋀ q) is equivalent to
(1) ~p
(2) p
(3) q
(4) ~q
Darjeeling District of West Bengal at a Glance
| Lok Sabha Constituencies in Darjeeling district, West Bengal (MP Constituencies) | Darjeeling |
| MLA Assembly Constituencies in Darjeeling district, West Bengal | Darjeeling Kalimpong Kurseong Matigara-Naxalbari Phansidewa Siliguri |
About Darjeeling District :
Darjeeling, the northernmost district of the Jalpaiguri Division, roughly resembles an inverted wedge with its base resting on Sikkim, its sides touching Nepal, Bhutan and the Jalpaiguri District of West Bengal. The district is located at 27 Deg. 13 Min. N to 26 Deg. 27 Min. North Latitude and 88 Deg. 53 Min. E to 87 Deg. 59 Min. East Longitude. The Area of the district is 3149 sq km. The district is divided into 4 Subdivisions 12 Blocks and 1534 Villages. The places of tourist interests in the districts are Darjeeling, Kalimpong, Kurseong means – the place of White Orchid, Mirik-a nest in the hills , Mungpoo, and Darjeeling Himalayan Railway
District at a Glance
- District –
- Headquarters –
- State
- Total –
- Rural –
- Urban –
- Population –
- Rural –
- Urban –
- Male –
- Female –
- Sex Ratio (Females per 1000 males) –
- Density (Total, Persons per sq km) –
- Assembly
- Loksabha –
- Official Website –
Tourist Places :
Tiger Hill :

Situated at an altitude of 2590 meters (8482 ft.) and 13 kilometers from the town, this spot has earned international fame for the magnificent view of the sunrise over the “Kanchanjunga” and the great eastern Himalayan Mountains. Even Mount Everest, the world’s highest peak, is visible from here. The hesitant rays of the early morning sun paint these peaks in pale gold
Batasia Loop and the War Memorial :



Kurukshetra District of Haryana at a Glance
| Lok Sabha Constituencies in Kurukshetra district, Haryana (MP Constituencies) | Kurukshetra |
| MLA Assembly Constituencies in Kurukshetra district, Haryana | Ladwa Pehowa Shahbad Thanesar |
About Kurukshetra District :
In the very first verse of Bhagwad-Gita (धर्मक्षेत्रे कुरुक्षेत्रे समवेता युयुत्सवः | मामकाः पाण्डवाश्चैव किम् अकुर्वत संजय ||), Kurukshetra is described as DHARAMKSHETRA i.e. ‘Region of righteousness’. Kurukshetra is a place of great historical and religious importance, revered all over the country for its sacred association with the Vedas and the Vedic Culture. It was here that the battle of Mahabharat was fought and Lord Krishna preached His Philosophy of ‘KARMA’ as enshrined in the Holy Bhagwad-Gita, to Arjuna at Jyotisar. According to Hindu mythology, the Kurukshetra is spread over, a circuit of about 48 KOS which includes a large number of holy places, temples and Sacred tanks connected with the religious events/rituals, Mahabharat War and Kurus, the ancestor of Kouravas and Pandavs. Kurukshetra is intimately related to the Aryan civilization and its growth all along the sacred river Saraswati.
It is believed that all the holy waters of all sacred rivers flow/converge into Kurukshetra’s Sannehit Sarovar, at the time of Somavati Amavasya & Solar eclipse. It is believed that those who visit this area reside here, take bath in the tanks, or die in Kurukshetra go to heaven after death. The Mahabharata states that one who dies at Kurukshetra attains salvation after death. It is said that the Almighty God after having perfomed, divine, yajnas created the universe here.
It is the land where the sage Manu penned his ‘Manusmriti’ and where learned ‘rishis’ compiled the Rig Veda and Sama Veda.Kurukshetra is named after King Kuru, who also performed a supreme sacrifice to bring prosperity to the land and his people.
District at a Glance
- District –
- Headquarters –
- State
- Total –
- Rural –
- Urban –
- Population –
- Rural –
- Urban –
- Male –
- Female –
- Sex Ratio (Females per 1000 males) –
- Density (Total, Persons per sq km) –
- Assembly
- Loksabha
- Official Website –
Tourist Places :
Brahma Sarovar :

Brahma Sarovar, as its name suggests, is a water tank in Thanesar in Haryana. It is considered sacred by Hindus and is incredibly beautiful. It is said that the water inside the tank is sacred and used by people internally as well as externally to take a bath and attain salvation. It has been currently renovated and equipped with modern state-of-the-art facilities. The tank has the dimensions of 3600 length and 1500 breadth. It has been given a rectangular shape.
Legend has it that the universe was created by Lord Brahma from the land of Kurukshetra after yajna took place. This Brahma Sarovar is believed to be the support of the civilisation and has also been mentioned in the eleventh century AD memory of Al Beruni who was also called Kitab-ul-Hind
Krishna Museum :

Founded in 1987, Krishna Museum houses various artifacts of Lord Krishna and Krishna’s incarnations from 1st Century AD to 11th Century AD. The museum housing six galleries also showcases the statues in the forms as described in the Bhagavata Purana and Mahabharata.
The exhibits in the galleries consist of exquisite woodcarvings, wooden panels, bronze casting, ivory works, palm- leaf etchings, stone sculptures, archaeological artifacts and miniature paintings. There is also a tableaux made from Papier-mache and clay, based on Bhagavata and Mahabharata
Sthaneshwar Mahadev :

It is said that the Pandavas obtained the blessings of Lord Shiva in Sthaneshwar Mahadev Temple. The tank in the premises of the temple is believed to possess healing properties and has also healed Banasura’s leprosy.
Archeologists trace the architecture of the temple to Sthaneshwar, an ancient capital of Harsha Vardhana. One can see the roof of the temple shaped like an amla dome with lofty pinnacles. The temple houses an ancient statue of the Shiva Linga which is believed to be the first idol of Shiva in the phallic form
Sthaneshwar Mahadev Temple :

It is said that the Pandavas obtained the blessings of Lord Shiva in Sthaneshwar Mahadev Temple. The tank in the premises of the temple is believed to possess healing properties and has also healed Banasura’s leprosy.
Archeologists trace the architecture of the temple to Sthaneshwar, an ancient capital of Harsha Vardhana. One can see the roof of the temple shaped like an amla dome with lofty pinnacles. The temple houses an ancient statue of the Shiva Linga which is believed to be the first idol of Shiva in the phallic form
Karnal District of Haryana at a Glance
| Lok Sabha Constituencies in Karnal district, Haryana (MP Constituencies) | Karnal |
| MLA Assembly Constituencies in Karnal district, Haryana | Assandh Gharaunda Indri Karnal Nilokheri |
About Karnal District :
Karnal is one of Historical Districts of Haryana. It is also known as a city of ‘Daanveer Karn’. It is known all over the world for production of Rice, Wheat and Milk. It is also known for agriculture research Institutions like NDRI, CSSRI, Wheat Research Directorate, National Bureau of Animal Genetics Resources, Sugarcane Breeding Institute etc
Karnal is important city on Delhi Ambala Rail Line & Sher Shah Suri Marg (G.T.Road), connected with all important places in the country. It is 123 Kilometer from Delhi & 130 Kilometer from Chandigarh. Karnal District lies on the western Bank of river Yamuna which once flows about 11 Kilometer. to the east forming eastern boundary of the district. The river Yamuna separates Haryana from Utter Pardesh. The Karnal Distt. including Panipat lies between 29’09’50” and 29’50’ North latitude and 76 31′ 15″ and 77 12’45” East longitude, its height from sea level is between 235 and 252 meters. The Karnal Distt. is surrounded by Kurukshetra District on its north-west, jind & Kaithal Distt. on its west, Panipat Distt. on its south and Utter Pradesh on east.
Yamuna River forms eastern boundary of the district and flows from north to south. The district is a part of the Ganga-Sindus (Indo-Gangestic) plains and has a well spread net work of western Yamuna canal. Its geographical area has been divided in to three agroclimatic regions, Khadar, Bhangar and Nardak belt. Khadar starts from Indri-Karnal road one mile away from Karnal covering the area in between Yamuna river and National Highway Road No.1 upto Patti-Kalyana village. Bhangar area starts from west of Khadar area covering Gharaunda, development block. The nardak area lies in Nissing, Nilokheri and Assandh development block. However, its water is saline and not fit for irrigation
District at a Glance
- District –
- Headquarters –
- State
- Total –
- Rural –
- Urban –
- Population –
- Rural –
- Urban –
- Male –
- Female –
- Sex Ratio (Females per 1000 males) –
- Density (Total, Persons per sq km) –
- Assembly
- Loksabha
- Official Website –
Tourist Places :
Cantonment Church Tower :

Being a fine example of the unique architectural style of the British era, Cantonment Church Tower stands tall in Karnal. The tower is about thirty-five meters high and has an ornamental cross on the top. The tower is visible from a radius of 7 km around the church. The church was dedicated to St. James, a disciple of Jesus Christ. The church got dismantled when the cantonment was shifted from Karnal to Ambala however the tower was permitted to stand here. Adjacent the tower is a cemetery of the European soldiers on the left side. Indian National Trust for Art and Cultural Heritage has certified this Cantonment Church Tower to be a historic monument of the country.
Qualander Shah’s Tomb :
 Built in the memory of Bo-Ali-Qualander Shah, the famous Muslim sage, this place of honour was constructed by Ghias-ud-din Tughlaq, the ruler of Delhi. The well sculpted memorial was constructed in marble. The tomb is important because of the stories that are related to Qualander Shah. This Sufi sage was famous for his new-age thinking and his ideas that have been respected and appreciated by people of all religions. The saint was said to be blessed with miraculous powers. The tomb premises are fenced by walls and hoses beautiful fountains and lush garden surrounding the tomb.
Built in the memory of Bo-Ali-Qualander Shah, the famous Muslim sage, this place of honour was constructed by Ghias-ud-din Tughlaq, the ruler of Delhi. The well sculpted memorial was constructed in marble. The tomb is important because of the stories that are related to Qualander Shah. This Sufi sage was famous for his new-age thinking and his ideas that have been respected and appreciated by people of all religions. The saint was said to be blessed with miraculous powers. The tomb premises are fenced by walls and hoses beautiful fountains and lush garden surrounding the tomb.
Karnal Fort :
Built in the mid eighteenth century by Raja Ganpat Singh, Karnal Fort now houses an important office of the city. Being conquered by different Emperors in different eras, Karnal Fort has seen glorious victories and unimpressive declines of the rulers. Conquered by the Marathas from Raja Bhag Singh, Karnal Fort has been a witness of the tussles between the Sikhs and the Marathas until Karnal was overtaken by the British. The fort was used a jail during the initial British-Raj. The stately construction of the fort is outstanding and it is known as the Old Fort by the locals
Pukka Pul :
Pukka Pul is also known as Sayad’s Shrine is located at a distance of 7 km from the main city of Karnal and is considered to be a sacred monument by the Muslims. The shrine is in the vicinity of the Mughal Bridge and is known for having powers to counter the ghostly spirits and cure serious diseases. Every Thursday the shrine is illuminated with lamps. Devotees around the world come here to seek the blessings so as to lead a positive life ahead.
Karnal has been a city of historical importance from the time of Mahabharata. The place has been a spectator of different eras and been a part of the Indian history. Karnal or the Karnabhoomi will leave you mesmerised with the ancient stories that the city contains
Anita Chaudhry

Hon’ble Mrs. Justice Anita Chaudhry
She was Born on 31.12.1956. She belongs to a family of illustrious lawyers. She graduated from Govt. College for Women Chandigarh and got her L.L.B. Degree from Panjab University, Chandigarh in 1979. She was enrolled as an Advocate on 3.8.1979 and practised till the end of December 1979. She Joined Haryana Judicial Service on 2.1.1980. She was promoted as Additional District Judge in 1994. She went on deputation as Chief Legal Advisor with Delhi Development Authority, Delhi from 1997 upto 2000 and was promoted as District and Sessions Judge in 2005. She served as District and Sessions Judge at Hisar, Faridabad, Bhiwani and Panchkula. She was elevated as Additional Judge of Punjab and Haryana High Court, Chandigarh on 20.06.2013.
Amol Rattan Singh

Hon’ble Mr. Justice Amol Rattan Singh
Born on 19.08.1960 at Hoshiarpur. He did post-graduation- M.A. (English) in 1981 and L.L.B. from Panjab University, Chandigarh, in 1985. He was enrolled as an Advocate on 30.6.1985 and handled Service & Civil matters. He was appointed as Additional (Junior) Counsel for the State of Haryana at the Supreme Court of India in 1994- 1995, Assistant Advocate General, Haryana in June 1995 and Deputy Advocate General, Haryana in 2004.Thus remained Haryana State Law Officer for 10 years. In the above capacities handled all kinds of litigation for the State in Civil and Service matters, in the High Court and Central Administrative Tribunal, Accident Claims, Public Interest litigation, Land Acquisition, Service matters, Labour related matters, etc. Remained Counsel for the Koul Commission (investigating the Police firing incidents at Bahadurgarh, District Jhajjar), for a short period. Thereafter, he was appointed as Additional Advocate General, Punjab, on 7.9.2005 and continued as such till 20.12.2012. In this capacity, mainly handled sales tax (VAT) matters and Public Interest Litigation, alongwith other, varied, miscellaneous matters. Sworn in as an Additional Judge of the Punjab and Haryana High Court on 21.12.2012.
Inderjit Singh

Hon’ble Mr. Justice Inderjit Singh
His Lordship was born on October 24, 1957, did his LL.M. in 1982 from Panjab University, Chandigarh. Joined Punjab Civil Services (Judicial Branch) in 1983. Promoted as Additional District & Sessions Judge in 1999 and served as such at different stations. Promoted as District & Sessions Judge in April 2006 and posted at Patiala. Remained District & Sessions Judge at Faridkot and Jalandhar also. He was elevated as Additional Judge of Punjab and Haryana High Court on June 15, 2012 and thereafter as Permanent Judge on 19.12.2014.
JEE Main 2016 Preparation Tips
Preparation for JEE Main 2016:
As all Indian aspirants know, Joint Entrance Examination(JEE) is a national level entrance test conducted for the admission to the various government and private institutions like NITs (National Institute of Technology) and IIITs (Indian Institute of Information Technology). Students who score well in JEE Main exam will be able to get admission in Engineering and technical courses in top most colleges of the country.
About JEE Exam:
Joint Entrance Examination (JEE) is a two tier examination in which first stage of exam is “JEE Main” and the second stage of the exam is said to be “JEE Advanced”. JEE Main is the entrance test which is a gateway for the B.Tech courses offered by the famous institutes like IIITs and NITs. Whereas, those who clear JEE Main exam are eligible to take the JEE Advanced entrance test which is a gateway for engineering courses in the institutes like IITs (Indian Institute of Technology) (Ultimate dream institute for many Indian students)
But before start preparing for JEE Main 2016, it is important to know the following details about the Joint Entrance Examination Main 2016.
- Candidates should have studied Physics and Mathematics in their Class 12
- They must have compulsorily studied any of the following subjects: Computer Science, Bio-technology, Chemistry and Biology and should have secured minimum 50% of marks in all the subjects.
- Candidates must have born on or after October 1991.
- Candidates must have passed Class 12 or equal qualifying exam in 2014 or 2015.
- You can download JEE Main 2016 Admit card on March 2016(Tentative date).
- Tentative dates for JEE Main 2016 exam are:
Online Test: April 2016
Offline Test: April 2016
- You can check the complete Application procedure for JEE Main 2016 in the official portal of JEE Main 2016.
How to Prepare for JEE Main 2016?
Please ensure the Pattern and Syllabus for the JEE Main 2016 examination. In order to score well in this exam, you must be very clear about the pattern and syllabus of the examination. Also please note the following details which are very important for the candidates who are taking this exam.
Please make note of the following link for checking the syllabus of JEE Main 2016:
http://www.jeesyllabus.in/jee-syllabus
- Total duration for the JEE Main 2016: 3 hours
- Total Questions: 90
- Maximum marks: 360
- Paper 1 sections: Physics, Chemistry and Mathematics (BE/B.Tech)
Objective type of questions and equal marks for all the above subjects. This section can be written using pen and paper based or computer based.
- Paper 2 sections: Physics, Chemistry & Drawing and Aptitude test(B.Arch/Planning)
Objective type of questions in above subjects including aptitude questions and drawing. This section can be written only using pen and paper.
- Marks for correct answer: +4
- Marks for wrong answer: -1
- Zero marks will be considered for “No answer”
You need to download the application form the official JEE apex board. Candidates who are going to take up JEE Main 2016 exam must note that Paper I will be held both in online and offline mode. Please choose the mode in which you like to appear.
For guaranteed success in the JEE Main 2016 exam, it is important to prepare in the following manner
- Plan according to each subject.
- Prepare
- Practice
- Revise
Plan according to each subject:
This is very important thing to score well in this exam. Give equal importance to all subjects and plan accordingly. You can also refer the following books.
Physics:
D.C.Pandey series
36 years IIT asked by Arihant
H.C.Verma volume 1 and 2
Maths:
R.D.Sharma Objective Volume 1 and 2
Play with graphs by Amit M aggarwal
36 years IIT asked by Arihant
Chemistry:
Organic: Morrison and Boyd
Physical: R.C.M
Inorganic: O.P.Tondon
36 years IIT asked by Arihant
Prepare:
- Plan and schedule your subjects. Schedule atleast 2 hours for every subject and learn according to that. More you strive hard, more you can score high in JEE Main 2016.
- Start to learn new things at the beginning since it gives hopes and concentration in the subjects.
- Give a ten minutes break after you complete each subject and then start with the next one.
- Revise your earlier portions every morning and then start the present day’s portion.
- If it is mathematics, please don’t hesitate to try the same in your rough note. Things change when you try on your own.
- Try to spend more time for difficult subjects and make them thorough and confident.
- Try to refer to previous years question papers like JEE Main 2013, JEE Main 2014, JEE Main
- You can find such question papers with solutions in the following links
https://entranceindia.com/jee-main-free-practice-papers/
Practice:
However your study method is, the most important part of your learning is practice. The more you sweat in practice, the less you bleed in battle.
As said above, practice your subjects very carefully.
- For mathematics, try to solve the solution on your own. Try to solve everything without referring the books.
- For chemistry or Physics, try to solve the equations on your own.
- For other subjects plan and practice accordingly.
- Never postpone your schedule. Please try to complete the scheduled syllabus within the same day.
Revise:
Revise your previous lessons daily and also schedule to revise once in every week. This will Brush up your memory and make you feel more comfortable with the subjects.
Special Tips for JEE Main 2016:
- If you have already started taking coaching for JEE Main in any coaching centre, be regular and keep practicing.
- If you have not yet started to go to coaching class, it’s never too late. Start preparing right now.
- Always be in contact with your seniors. It’s good to know their experience facing the JEE Main
- Around 45% of JEE Main aspirants wish to take online coaching than any direct coaching centre.
- You can make best use of internet by taking part in the mock test, watching video lectures, taking online exams, etc.
You can check the following link for taking mock test of JEE Main 2015
https://entranceindia.com/jee-main/jee-main-model-papers-at-a-glance/
- Please make note of all the important topics in all subject. Concentrate more on that.
Hope these tips will help you crack the JEE Main 2016 exam. Be confident and cool. Make efficient use
of time. All the best for cracking JEE Main 2016!!
JEE Main 2016 Information Bulletin
JEE Main Exam:
Joint Entrance examination (JEE Main) is a very important national level engineering entrance exam for the admission to the top most engineering colleges in India. JEE Main is conducted by the Central Board of Secondary Education (CBSE) which declared JEE Main exam as the common entrance examination in the place of AIEEE and IIT-JEE.
JEE Main is conducted in two types. JEE Advanced which is carried out for the admission to the top Indian Institute of Technology (IIT) and JEE Main is carried out for the admission to the Indian Institute of Information Technology (IIIT) , National Institute of Technology (NIT) and Central Funded Technical Institute (CFTI).
JEE Main consists of two papers such as
Paper 1 which is for the admission to the B.E and B.Tech
Paper 2 which is for the admission to the B.Arch and B. planning
Upcoming JEE main exam and Important dates:
- JEE Main online application starts from first week of November 2015
- Last date for the online application: Last week of December 2015
- Application checking: January 2016
- Issuance of Admit card: March 2016 onwards
- JEE Main pen and paper based test: First week of April, 2016
- JEE Main computer based test: Second or third week of April, 2016
- Displaying OMR sheet and answer key on: Fourth week of April, 2016
- Result declaration: First week of July 2016
- Availability of score card: As soon as the results are declared, score cards will be available from official site of JEE Main.
How to apply for JEE Main 2016?
- Visit JEE Main official website http://jeemain.nic.in/webinfo/welcome.aspx during the first week of November, 2015.
- Register for JEE Main You will be getting a username and password to your registered email id.
- Now log in with that username and password. Fill in all the details such as name, father’s name, choice of test city, paper preferred, application number, roll number of 12th board examination, certificates of 10th and 12th, etc.,
- Upload your digital photograph along with your left thumb impression in JPEG format.
- Pay the application fees either through debit or credit card.
- Click on submit button.
- Take a copy of confirmation page.
Eligibility criteria:
- General and OBC candidates must have born on or after October 1, 1991.
- There is no minimum age limit for JEE Main exam
- Candidate must have cleared 12th board exam or equivalent qualifying exam with PCM group as their major subjects.
- He/she must have cleared all major subjects with more than 50% of marks.
- Students are allowed maximum of three attempts in JEE Main exam
Pattern and Syllabus:
JEE Main exam are conducted both in online and offline mode.
Online vs offline exam:
- Online test is the most preferred test mode for most of the students. This is because, in online mode it is easy to change the answer (By just tapping other radio button), facility to check the quick view of unanswered questions, navigation between the questions, etc.,
- Students taking online exam will get more time for JEE Main preparation since they are conducted only after offline exam.
- Online exam application fee cost less than offline exam.
- Even exam authorities are trying to bring more students in online mode which helps to cut down money and time.
Pattern for JEE Main 2016:
Total duration of the exam: 3 hours
Total questions: 90
Maximum marks: 360
Each correct attempt carries +4 mark
Each incorrect attempt carries -1 mark
No marks for unanswered questions
Paper 1 consist of Mathematics, Physics, Chemistry
Paper 2 consist of Physics, Chemistry, Drawing and aptitude test, Mathematics
Syllabus:
For AIPMT Syllabus and free practice papers with year wise you can follow the below url:
https://entranceindia.com/jee-main-free-practice-papers/
Admit card for JEE Main 2016:
Admit card for JEE Main 2016 will be available from March 2016 onwards. This Admit card contains important details of the student such as name, father’s name, date of birth, choice of city, paper choice, examination date, venue, etc. This is a very important document which must be kept safely even after the exam gets over.
You can download the admit card from the official site of JEE Main (i.e., http://www.jeemain.nic.in)
While downloading, students have to provide their application number and password which you would have received during the time of registration. Admit card is available only to those who have updated their board exam roll number while registration.
If you have not updated your roll number, please visit the following link:
https://entranceindia.com/jee-main-admit-card/
Result announcement:
JEE Main is planned to be conducted on April, 2016. Results are expected to be declared on first week of July, 2016. On the basis of the marks secured in JEE Main and 12th board exam (60% and 40% marks respectively) separate rank list will be declared for B.E and B.Planning courses.
Ranks cards will be available for download which consist of details such as:
- Category rank of the candidate
- State rank of the candidate
- All India rank of the candidate
Counselling for JEE Main:
CBSE releases the meritorious students list as soon as the results are announced. JEE Main counselling is to be done through Joint Seat Allocation Authority (JOAA) which allows students to select their seat preference and courses according to the ranks secured.
As soon as the results are announced, you can find the official announcement of Counselling for JEE Main in the website of JOAA. Only those candidate who has secured higher marks than the cut-off benchmark, will be called for the counselling process.
Steps for counselling:
- JEE Main counselling registration
- Fill your choice of college and course
- Locking of your choice
- Allotment of seat
- Payment of fees
- Reporting to the reporting centres
- Reporting to the allotting institute
For the year 2015, JOAA was about to fill 10006 in IIT’s, 17390 seats in NIT’s, 2228 seats in IIIT’s and 3741 seats in the GFTI’s.
Students, who have not selected in IIT’s and NIT’s don’t panic. There are lot of best private and Government colleges in India which accepts JEE Main scores.
Other option is, if you are among the top 1, 50,000 students in JEE Main ranks, there is also a possibility to attend JEE Advanced examination which leads to the admission of top IIT’s of the country.
Past Exam Papers JEE Main 2013 Mathematics (offline)
[LDAdvQuiz 17]
Past Exam Papers JEE Main 2013 Chemistry (offline)
[LDAdvQuiz 18]
Past Exam Papers JEE Main 2013 Physics (offline)
[LDAdvQuiz 16]